ΦΥΣΙΚΟΡΑΜΑ

Τι είναι η Ε.Ο.Μ.Κ.

Διαγράμματα  α-t,  υ-t,  x-t  στην Ε.Ο.Μ.Κ.

Ασκήσεις

Α.  Θεωρία

Μια κίνηση ονομάζεται ευθύγραμμη ομαλά μεταβαλλόμενη όταν η επιτάχυνση α είναι σταθερή.

Σε αυτή την περίπτωση ισχύουν τα παρακάτω :

• Σε ίσους χρόνους έχουμε ίσες μεταβολές ταχύτητας
• Η επιτάχυνση είναι σταθερή
• Η μέση επιτάχυνση είναι ίση με την στιγμιαία επιτάχυνση

• Η ταχύτητα υ δίνεται από την σχέση     $\upsilon ={\upsilon }_0+\alpha t$$\mathrm{({\rm N}ό\mu o\varsigma \; \tau \eta \varsigma \; \tau \alpha \chi ύ\tau \eta \tau \alpha \varsigma )}$

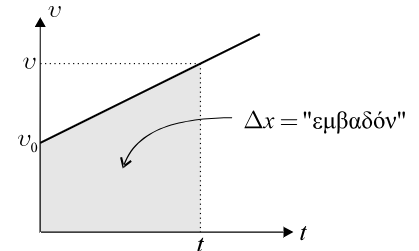
Παρατήρηση 1. H παραπάνω εξίσωση παριστάνει ευθεία σε ένα διάγραμμα $\upsilon -t$. Η Μετατόπιση στο χρονικό διάστημα $t=0$ έως $\mathrm{t=}$ υπολογίζεται από το εμβαδό του σχήματος που περικλείεται από :

• • • τον άξονα του χρόνου
    • την αρχική και την τελική χρονική στιγμή
    • και το γράφημα της ταχύτητας.

Παρατήρηση 2. Αν δεν γνωρίζουμε το χρόνο t αλλά μόνο τη μετατόπιση Δx (η την απόσταση s) της κίνησης υπολογίζουμε την ταχύτητα υ από την  εξίσωση      υ²=υ₀²+2αΔx

• Η μετατόπιση s δίνεται από την σχέση   $s={\upsilon }_{0}t+\frac{\mathrm{1/}}{2}\alpha t^2$$\mathrm{({\rm N}ό\mu o\varsigma \; \tau o\upsilon \; \delta \iota \alpha \sigma \tau ή\mu \alpha \tau o\varsigma )}$

H παραπάνω εξίσωση για την μετατόπιση ισχύει σε κάθε περίπτωση (ανεξάρτητα από το πρόσημο της αρχικής ταχύτητας και της επιτάχυνσης). Στο παρακάτω σχήμα φαίνεται μια περίπτωση όπου η αρχική ταχύτητα είναι θετική και η επιτάχυνση αρνητική.

• Το διάγραμμα ταχύτητας – χρόνου είναι ευθεία της οποίας η κλίση της (εφθ) μας δίνει την επιτάχυνση.
• Το διάγραμμα επιτάχυνσης – χρόνου είναι ευθεία παράλληλη του άξονα των χρόνων
• Το διάγραμμα θέσεως – χρόνου είναι παραβολή.
• Η συνισταμένη των δυνάμεων που ασκούνται στο σώμα είναι διάφορη του μηδενός.

Διακρίνουμε δύο κατηγορίες μεταβαλλόμενης κίνησης, την επιταχυνόμενη και την επιβραδυνόμενη.

1. Ευθύγραμμη ομαλά επιταχυνόμενη κίνηση

Μια κίνηση χαρακτηρίζεται ως επιταχυνόμενη όταν αυξάνεται το μέτρο της ταχύτητας ή όταν τα διανύσματα της επιτάχυνσης και της ταχύτητας να έχουν την ίδια φορά.

Στα παρακάτω διαγράμματα απεικονίζεται μια τέτοια κίνηση.

Παρατηρούμε ότι τη χρονική στιγμή t=0, το σώμα βρίσκεται στο σημείο x=0 και κινείται με αρχική ταχύτητα υ₀=3^m/_s.  Εκείνη τη στιγμή του ασκείται αποκτά επιτάχυνση α=2_^m/s²  και βλέπουμε η ταχύτητά του αυξάνεται γραμμικά. Το διάγραμμα x-t της κίνησής του είναι παραβολή.

2. Ευθύγραμμη ομαλά επιβραδυνόμενη κίνηση

Μια κίνηση χαρακτηρίζεται ως επιβραδυνόμενη όταν το μέτρο της ταχύτητας ελαττώνεται ή όταν τα διανύσματα έχουν αντίθετη κατεύθυνση.

Συχνά γίνεται η παρερμηνεία πως αν η επιτάχυνση είναι αρνητική τότε η κίνηση είναι επιβραδυνόμενη αυτό είναι σωστό μόνο στην περίπτωση εκείνη που ταυτόχρονα η ταχύτητα είναι θετική.

Στα παρακάτω διαγράμματα απεικονίζεται μια επιβραδυνόμενη κίνηση.

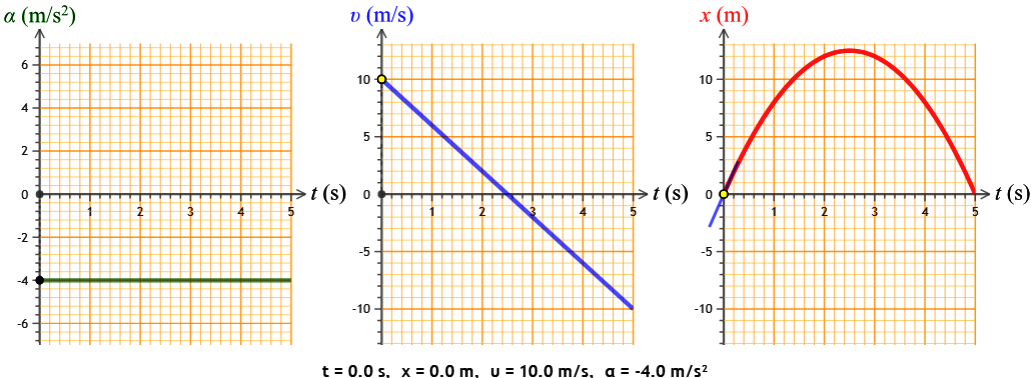
Παρατηρούμε ότι τη χρονική στιγμή t=0, το σώμα βρίσκεται στο σημείο x=0 (αρχή των αξόνων) και κινείται με αρχική ταχύτητα υ₀=+10^m/_s.  Εκείνη τη στιγμή του ασκείται μια δύναμη και αυτό αποκτά επιβράδυνση α=-4_^m/s²  και βλέπουμε ότι η ταχύτητά του μηδενίζεται (το σώμα σταματάει στιγμιαία) και ακολούθως αυτή αλλάζει φορά μέχρι να γίνει  υ₀=-10^m/_s,  δηλαδή επιταχύνεται προς την αντίθετη κατεύθυνση. Επίσης το διάγραμμα x-t της κίνησής του είναι μη γραμμικό.

Β.  Προσομοιώσεις

1.  Προσομοίωση Μελέτης της Ε.Ο.Μ.Κ.

(Για να μεταβάλλουμε την επιτάχυνση του σώματος μπορούμε να σύρουμε το διάνυσμα της επιτάχυνσης, το διάγραμμα της επιτάχυνσης – χρόνου ή να αλλάξουμε την κλίση του διαγράμματος ταχύτητας – χρόνου. Για να μεταβάλλουμε την αρχική ταχύτητα του σώματος μπορούμε να σύρουμε το διάνυσμα της ταχύτητας, το κίτρινο σημείο στο διάγραμμα ταχύτητας – χρόνου. Για να μεταβάλλουμε την αρχική θέση του σώματος μπορούμε να σύρουμε τον μοτοσυκλετιστή, τον άξονα της κίνησης ή το κίτρινο σημείο στο διάγραμμα θέσεως – χρόνου. Για να μεταβάλλουμε τον χρόνο θα πρέπει να σύρουμε τα μαύρα σημεία σε ένα από τα διαγράμματα κάποια χρονική στιγμή. Αν επιλέξουμε ρυθμίσεις μπορούμε να μεταβάλλουμε τις κλίμακες στα διαγράμματα και στον άξονα κίνησης.)

2.   Προσομοίωση Μελέτης Διαγραμμάτων Ε.Ο.Μ.Κ.

(Μπορούμε να σύρουμε τα κίτρινα σημεία ώστε να φτιάξουμε το επιθυμητό διάγραμμα. Έχουμε την δυνατότητα να μεταβάλλουμε τις κλίμακες και να σύρουμε τον άξονα του χρόνου στα διαγράμματα. Μπορούμε να μεταβάλλουμε το πλήθος των σημείων από τον αντίστοιχο δρομέα.)

Γ.  Εφαρμογές

Εφαρμογή διαγραμμάτων

Στην παραπάνω προσομοίωση να βρείτε την επιτάχυνση α του μοτοσυκλετιστή.

Ασκήσεις στην Ομαλά Επιταχυνόμενη Κίνηση

Ασκήσεις στην Ομαλά Επιβραδυνόμενη Κίνηση