Δοκιμαστικά θέματα live

Ακολουθούν μερικά ενδεικτικά θέματα του διαγωνισμού.

1ο Θέμα
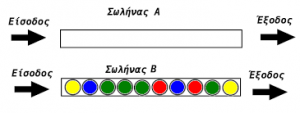
Τίτλος: Οι σωλήνες

2ο Θέμα

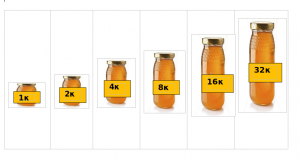
Τίτλος: Το μέλι

Ο Γουίνι (το αρκουδάκι) θέλει να αδειάσει 51 κιλά μελιού σε γυάλινα βάζα διαφορετικής χωρητικότητας, με την προϋπόθεση ότι όλα θα γεμίσουν.

Ερώτηση

Ποιος είναι ο μικρότερος αριθμός βάζων που μπορεί να χρησιμοποιήσει;

1. 4 βάζα

2. 3 βάζα

3. 2 βάζα

4. 5 βάζα

---

3ο Θέμα

Τίτλος: Μελισσοπλοήγηση

Ερώτηση
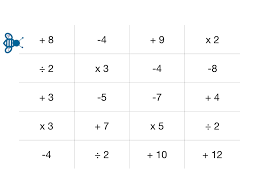
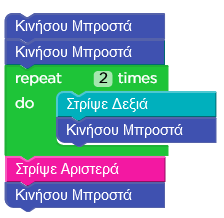
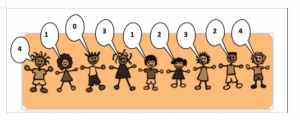
Η μελισσούλα του διαγωνισμού μας είναι έτοιμη να μαζέψει γύρη  από τον πίνακα που έχει μπροστά της. Αν υποθέσουμε ότι ξεκινάει χωρίς γύρη, από το σημείο που φαίνεται στην παραπάνω εικόνα, πόση γύρη θα έχει μαζέψει όταν θα έχει ακολουθήσει τις παρακάτω εντολές:

 

Α. 12
Β. 9
Γ. 4
Δ. 7

 

---

4ο Θέμα

Τίτλος: Σταματάμε τον Εκφοβισμό – Λέμε την Αλήθεια

Σε ένα σχολείο, κατά τη διάρκεια σχολικής εκδρομής, μία ομάδα μαθητών παρενόχλησε έναν μαθητή της Α΄ τάξης.  Την επόμενη μέρα, ο υπεύθυνος καθηγητής κάλεσε 9 μαθητές που ήταν παρατηρητές στο περιστατικό. Μετά από συζήτηση με τα παιδιά,  διαπίστωσε ότι κάποιοι μαθητές λένε πάντα την αλήθεια και κάποιοι λένε πάντα ψέματα.  Για να εντοπίσει αυτούς που λένε την αλήθεια, έκανε την παρακάτω ερώτηση σε κάθε μαθητή:

Πόσοι από τους 9 παρατηρητές είπαν την αλήθεια για το περιστατικό?

…και πήρε τις παρακάτω απαντήσεις :

Ερώτηση

Πόσοι μαθητές λένε την αλήθεια;

1. 3 μαθητές

2. 1 μαθητής

3. 4 μαθητές

4. 2 μαθητές

Α.2
Β.3
Γ.6
Δ.13

6ο Θέμα

Τίτλος: Ποιο κουτί έχει τα χρήματα;

Αν μία μόνο επιγραφή λέει την αλήθεια, μπορείτε να βρείτε ποιο κουτί περιέχει τα χρήματα;

Α. Το 1ο κουτί
Β. Το 2ο κουτί
Γ. Το 3ο κουτί

7ο Θέμα

Τίτλος: Ο αγώνας

Πέντε φίλοι έκαναν έναν αγώνα. Ο Χρύσανθος τελείωσε πιο γρήγορα από τον Κωνσταντίνο. Η πιο μικρή διαφορά στους τελικούς χρόνους ήταν ανάμεσα στον Κωνσταντίνο και τον Γιώργο. Η πιο μεγάλη διαφορά στους τελικούς χρόνους ήταν ανάμεσα στον Γιώργο και την Αργυρούλα. Ο Παναγιώτης τελείωσε ή στην πρώτη ή στην 3η θέση.

Ποιος τερμάτισε στην 3η θέση;

Α. ΧΡΥΣΑΝΘΟΣ
Β. ΚΩΝΣΤΑΝΤΙΝΟΣ
Γ. ΓΙΩΡΓΟΣ
Δ. ΑΡΓΥΡΟΥΛΑ
Ε. ΠΑΝΑΓΙΩΤΗΣ

8ο Θέμα

Τίτλος: Τα μολύβια

Έστω μία κασετίνα έχει από 1 ως 10 μολύβια. Σκοπός σου είναι να μαντέψεις πόσα ακριβώς μολύβια έχει.
Αν μου πεις έναν αριθμό, μπορώ να σου απαντήσω αν ο αριθμός των μολυβιών της κασετίνας είναι μικρότερος, μεγαλύτερος ή ίσος με τον αριθμό που είπες.
Ποιος είναι ο μικρότερος αριθμός από προσπάθειες που μπορείς να κάνεις, ώστε σίγουρα να βρεις τον αριθμό των μολυβιών της κασετίνας;

Α. 3
Β. 4
Γ. 5
Δ. 10

9ο Θέμα

Τίτλος: Αριθμοκυψέλες

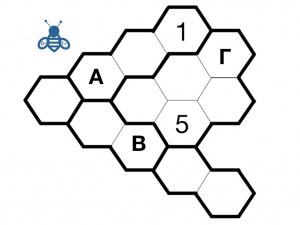
Η μελισσούλα του διαγωνισμού μας θέλει να γεμίσει την κυψέλη της με αριθμούς. Οι κανόνες που πρέπει να ακολουθήσει είναι οι εξής:

Κάθε περιοχή (με τις έντονες γραμμές), πρέπει να περιέχει από το 1 μέχρι τον αριθμό των εξαγώνων της περιοχής.
Ο αριθμός δεν πρέπει να είναι ίδιος με τον γειτονικό του αριθμό προς όλες τις κατευθύνσεις.

Η κυψέλη μας είναι όπως η παρακάτω:

Ποιοι αριθμοί αντιστοιχούν στις κυψέλες με τα γράμματα Α, Β και Γ.

i. Α: 2, Β: 1, Γ: 4

ii. Α: 3, Β: 1, Γ: 2

iii. Α: 4, Β: 3, Γ: 3

10ο Θέμα

Τίτλος: Ο Πύργος του Ανόι

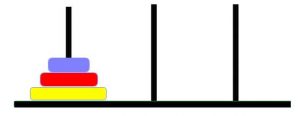
Ο παραπάνω πύργος του Ανόι αποτελείται από τρεις ράβδους και τρεις δίσκους διαφορετικών μεγεθών, οι οποίοι μπορούν να μετακινηθούν σε οποιαδήποτε ράβδο. Κάθε δίσκος δεν μπορεί να έχει από πάνω του δίσκο μεγαλύτερου μεγέθους.

Σκοπός είναι να μετακινηθούν όλοι οι δίσκοι από την αριστερή ράβδο στη δεξιά.

Πόσες μετακινήσεις δίσκων χρειάζεται να γίνουν;

Α. 3
Β. 5
Γ. 7
Δ. 9