Πότε όμως θα χρειαστεί να αντιμετωπίσεις ένα πρόβλημα που απαιτεί συγκέντρωση για πάνω από 30 δευτερόλεπτα; Κάθε, μα κάθε φορά.
Φέρτε στο μυαλό σας έναν μαθηματικό. Τι βλέπετε;
Ας κάνω την αρχή με μια αρκετά κοινή εικόνα. Είναι αργά το βράδυ. Μία φιγούρα είναι σκυμμένη πάνω από ένα γραφείο και γράφει βιαστικά σε ένα τετράδιο. Ο χώρος είναι γεμάτος από σκόνη γραφίτη και ψήγματα γόμας και υπάρχει έντονη σωματική οσμή. Αριθμοί και σύμβολα λάμπουν στο φως και μία αριθμομηχανή ξεκουράζεται κοντά σε μία στοίβα από βιβλία.
Αυτό που μόλις περιέγραψα δεν είναι απλώς ένα άδικο στερεότυπο. Τα μαθηματικά προσελκύουν αυτούς τους σκοτεινούς τύπους, που θα μπορούσαν άνετα να ζουν σε μία σπηλιά. (Προφανώς ξέρω, γιατί παρακολούθησα διαλέξεις τους.) Οπότε, όταν οι άνθρωποι ανακαλύπτουν ότι έχω σπουδάσει εφαρμοσμένα μαθηματικά, καταλαβαίνω γιατί ανασηκώνουν το φρύδι με απορία, λες και ανήκουμε σε διαφορετικά είδη.
Η πραγματικότητα, όμως, είναι λιγότερο εξωτική: Προτίμησα να σπουδάσω μαθηματικά, διότι ήμουν καλός σε αυτό και σκέφτηκα ότι οι δεξιότητές μου στην αριθμητική θα ενίσχυαν τις προοπτικές της καριέρας μου. Όπως αποδείχθηκε, δεν ήμουν αρκετά καλός. Ο Euler και οι ιδιοτιμές με διέλυσαν. Και παρόλο που η εξοικείωση με τη στατιστική αποδείχθηκε οριακά χρήσιμη, ποτέ μου δε χρησιμοποίησα το 99% των μεθόδων, των αποδείξεων και των θεωρημάτων που με τόσο κόπο μελετούσα εκείνα τα χρόνια.
Υπήρξαν τόσες πολλές στιγμές που ευχόμουν να είχα διαλέξει μια διαφορετική σχολή. Κάτι πιο εύκολο. Κάτι λιγότερο επώδυνο. Ορισμένες φορές, μίσησα τα μαθηματικά. Κι όμως, έξι χρόνια μετά, είμαι τόσο ευγνώμων που δεν τα παράτησα. Οι λόγοι δεν έχουν καμία απολύτως σχέση με τους αριθμούς. Έχουν να κάνουν με τη ζωή.
1. Δεν περιμένω να βρω την απάντηση στην πρώτη προσπάθεια
Σαν παιδί, πάντα πίστευα ότι στα μαθηματικά ήμουν άπιαστος. Αν η απάντησή μου δεν ταίριαζε με τις λύσεις του βιβλίου, πάντα κατηγορούσα το βιβλίο. «Θα είναι τυπογραφικό λάθος», μονολογούσα. Φυσικά, δεν ήταν ποτέ τυπογραφικό λάθος. Πάντα εγώ έσφαλλα.
Σαν φοιτητής, ανακάλυψα ότι η πρώτη λανθασμένη απάντηση ήταν μια σημαντική στιγμή – ένα απαραίτητο στραβοπάτημα στον δρόμο προς την αλήθεια. Αυτή η αντίληψη ριζώθηκε τόσο βαθιά μέσα μου, που αν έβρισκα τη λύση με την πρώτη προσπάθεια, σκεφτόμουν «πολύ τυχερός είμαι σήμερα».
Μπορεί να ακούγεται απαισιόδοξο, είναι όμως η αλήθεια. Ποτέ δεν απογοητευόμουν, γιατί απλώς ποτέ δεν περίμενα την εύκολη νίκη. Και αν κάποτε πετύχαινα τον στόχο με το πρώτο βέλος, εκπλησσόμουν ευχάριστα. Με τον καιρό έμαθα να αποδέχομαι τις αποτυχημένες προσπάθειες, και ως εκ τούτου έγινα πολύ πιο υπομονετικός.
2. Μπορώ να υπομένω τεράστιες ποσότητες εκνευρισμού
Η έλλειψη έμπνευσης σε έναν συγγραφέα δεν έχει κανένα κοινό με ένα δύσκολο μαθηματικό πρόβλημα και έχω αντέξει και τα δύο. Το συγγραφικό κενό συνήθως καταλήγει στη σκέψη ότι δεν είσαι αρκετά καλός για αυτό που προσπαθείς. Με τα μαθηματικά, είναι σαν όλο το σύμπαν να κοροϊδεύει την ανικανότητά σου.
Όταν πολλαπλασίαζα πίνακες, τραβούσα τα μαλλιά μου και τα έβλεπα να κυματίζουν πάνω σε χιλιοσβησμένες σελίδες χαρτιού. Αυτό σπάνια με βοηθούσε να πλησιάσω στη λύση, οπότε δικαίως σκεφτόμουν, «Ωραία, ποιο το νόημα όλου αυτού;».
Θυμάμαι τον βοηθό καθηγητή στο μάθημα της γραμμικής άλγεβρας να λέει κάποτε, «τα Μαθηματικά είναι πόνος». Συμφωνώ. Το να σπουδάζεις μαθηματικά σε φέρνει στα όρια του μαζοχισμού. Το μυστικό είναι να δέχεσαι τον πόνο με χαρά. Έμαθα να ευχαριστιέμαι τον εκνευρισμό, να τον αντιμετωπίζω σαν ένα παιχνίδι, όπου εγώ θα ήμουν πάντα ο τελικός νικητής.
Ως αποτέλεσμα, η ανοχή μου στην αγανάκτηση είναι πολύ υψηλότερη. Είμαι πεπεισμένος ότι οι σπόροι της υπομονής και της αντοχής φυτεύτηκαν και βλάστησαν μέσα σε εκείνα τα τετράδια μαθηματικών.
3. Αντιμετωπίζω τα προβλήματα πολύπλευρα
Όταν ήμουν παιδί, ο πατέρας μου είχε μια κόκκινη εργαλειοθήκη γεμάτη με κλειδιά, κατσαβίδια και διάφορα άλλα μαραφέτια. Ήταν τόσο μεγάλη, που για να τη σηκώσω, έπρεπε να την κρατήσω και με τα δύο χέρια.
Το να σπουδάζω μαθηματικά, ήταν σαν να συντηρώ αυτή την εργαλειοθήκη. Κάθε φορά που μάθαινα κάτι καινούργιο, αυτή η γνώση έμπαινε μέσα στο μεγάλο κόκκινο κουτί. Ποιος να ήξερε πότε θα μου φαινόταν χρήσιμη; Οι βαθιά θαμμένες μέθοδοι θα μπορούσαν κάλλιστα να είναι το καρυδάκι που θα χρειαζόμουν αργότερα.
Η επιστήμη των μαθηματικών στηρίζεται στη χρήση του σωστού εργαλείου τη σωστή στιγμή. Η τέχνη όμως είναι να γνωρίζεις εκ των προτέρων ποιο εργαλείο να πιάσεις κάθε φορά. Το πρόβλημα είναι ότι όταν ανακαλύπτεις συνεχώς μυστηριώδη αντικείμενα, είναι δύσκολο να αντιληφθείς ποιο εργαλείο ταιριάζει.
Σταδιακά έγινα επιδέξιος στο να δοκιμάζω κάθε είδους τακτική, συνήθως πελεκώντας ένα πρόβλημα από διαφορετικές γωνίες, ελπίζοντας σε μία σημαντική ανακάλυψη. Η χαρά που παίρνεις όταν λύνεις ένα πρόβλημα είναι αυτή που με κρατάει, και υπάρχουν λίγα μόνο καλύτερα συναισθήματα, από όταν το κλειδί επιτέλους ταιριάζει και η κλειδαριά ανοίγει.
4. Πάντα ελέγχω τη δουλειά μου
Το να ξέρεις πώς να λύνεις προβλήματα είναι το πρώτο βήμα. Το δεύτερο είναι να μην ξεγελιέσαι, νομίζοντας ότι γνωρίζεις περισσότερα απ’ όσα όντως γνωρίζεις.
Ο επηρμένος μαθηματικός είναι και ο απρόσεκτος. Οι σωστοί μαθηματικοί είναι σκεπτικιστές, είναι διστακτικοί ακόμα και προς τα ίδια τους τα ένστικτα. Ακόμα και αν ήξερα πώς να βρω τη λύση, πάντα θα προχωρούσα με προσοχή. Μία χαμένη υποδιαστολή και τα πάντα θα κατέρρεαν.
Κι όταν μάλιστα το έλυνα, πάντα ήλεγχα κάθε βήμα προσεκτικά, προσπαθώντας να εντοπίσω προβληματικές αιτιολογήσεις ή αβίαστα λάθη. Πολλές φορές, έλυνα το πρόβλημα με διαφορετικό τρόπο, ώστε να βεβαιωθώ ότι θα καταλήξω στο ίδιο αποτέλεσμα.
Τα μαθηματικά μού υπενθυμίζουν ότι δεν είμαι άτρωτος – επιρρεπής σε κάθε είδους αναποδιά και στραβοπάτημα. Ποτέ δεν πρέπει να βιάζομαι, γιατί το να περπατάς με προσοχή είναι καλύτερο από το να τρέχεις και να σκοντάφτεις. Και το ότι έφτασα απλώς σε μία απάντηση, δε συνεπάγεται απαραίτητα ότι είναι και η σωστή.
5. Εξασκώ την επιμονή μου
Ίσως να έχετε ακούσει το στερεότυπο ότι οι Ασιάτες είναι καλοί στα μαθηματικά. Ας υποθέσουμε ότι έχω ένα μεγάλο δείγμα και, σίγουρα, ορισμένοι Ασιάτες φοιτητές μαθηματικών είναι πολύ έξυπνοι. Ή, τουλάχιστον, εξυπνότεροι από εμένα. Δηλαδή υπάρχει κάποιο γονίδιο που προικίζει τους Ασιάτες με ταλέντο στα μαθηματικά; Πολύ αμφιβάλλω.
Μήπως οι Ασιάτες φοιτητές μεγάλωσαν έτσι, ώστε να είναι πιο επίμονοι από τους Αμερικανούς; Ίσως.
Σε μία διάσημη έρευνα, δόθηκε σε αμφιθέατρα πρωτοετών Αμερικανών και Ιαπώνων φοιτητών ένα αδύνατο πρόβλημα μαθηματικών. Οι Αμερικανοί φοιτητές τα παράτησαν σε λιγότερο από 30 δευτερόλεπτα, ενώ οι Ιάπωνες προσπαθούσαν για περίπου μία ώρα, πριν οι επιτηρητές τούς σταματήσουν, επιβεβαιώνοντας πως πρόκειται για πρόβλημα χωρίς λύση. (Πόσο βάναυσο!) Η μεγάλη διαφορά έγκειται στο ότι οι Ασιατικές κουλτούρες δίνουν προτεραιότητα στην εξάσκηση και την επιμονή στην εκπαίδευση, ενώ παράλληλα αποδέχονται ότι οι δυσκολίες είναι ένα μεγάλο κομμάτι της εκπαιδευτικής διαδικασίας. Στον Δυτικό κόσμο, η ιδέα της έμφυτης ευφυΐας προωθείται και επαινείται, ενώ υπονομεύεται η σημασία της δυσκολίας στην εκπαίδευση. Θα έλεγα ότι χαϊδεύουμε τα παιδιά μας. Δώστε σε έναν Αμερικανό μαθητή ένα πρόβλημα μαθηματικών και οι πιθανότητες λένε ότι θα παραπονεθεί κλαψουρίζοντας, βάζοντας μπροστά τη γνωστή κασέτα: «Μα πού θα μου χρησιμεύσει αυτό στον πραγματικό κόσμο;».
Το να απαντήσεις άμεσα σε αυτή την ερώτηση είναι λάθος. Πότε θα χρειαστεί να παραγοντοποιήσεις ένα πολυώνυμο «στον πραγματικό κόσμο»; Ίσως ποτέ, αγαπητό μου παιδί. Ειδικά με αυτή τη στάση.
Πότε όμως θα χρειαστεί να αντιμετωπίσεις ένα πρόβλημα που απαιτεί συγκέντρωση για πάνω από 30 δευτερόλεπτα; Κάθε, μα κάθε φορά!!!
Είμαι τόσο τυχερός που τα μαθηματικά με ώθησαν στο να εξασκήσω την επιμονή μου. Απέδωσε τεράστιους καρπούς αργότερα, παρόλο που ήμουν αρκετά ανώριμος, ώστε να το αναγνωρίσω τότε.
6. Ξέρω τι με κάνει χαρούμενο (και τι όχι)
Το μεγαλύτερό μου μάθημα από τα μαθηματικά ήταν και το πιο παράλογο: δεν είμαι φτιαγμένος γι’ αυτό. Παρόλο που σπούδαζα εφαρμοσμένα μαθηματικά ως 19χρονος, απογοητεύτηκα από την πραγματική εφαρμογή τους. Εγώ ήθελα να βγω έξω στον κόσμο και να κάνω πράγματα, όχι να είμαι βυθισμένος σε σετ ασκήσεων.
Έτσι, άρχισα να τα παρατάω. Στις εξετάσεις απέτυχα. Παρέδιδα μισοτελειωμένες εργασίες, αν παρέδιδα κάτι εντελώς. Η μόνη φορά που έβλεπα “A” ήταν στην αρχή του ονόματός μου.
Ήμουν απόλυτα ικανοποιημένος με το να βουλιάζω στη μαθηματική μετριότητα.
Και αυτό με τρομοκρατούσε. Διότι δεν μπορούσα να αγνοήσω αυτή τη φωνή μέσα μου που φώναζε: Δεν είσαι πλασμένος για αυτό.
Η αλήθεια είναι ότι τα μαθηματικά δε με παρακινούσαν. Το στομάχι μου έσφιγγε, όταν έμπαινα σε ένα αμφιθέατρο και περνούσα δίπλα από έναν πίνακα κιμωλίας. Μετά από κάθε εξεταστική, με τις μαθηματικές μεθόδους να κουδουνίζουν στο κεφάλι μου σαν ντέφι μέσα σε πλυντήριο, δεν μπορούσα παρά να σκέφτομαι, «Ωραία… Και τώρα τι να κάνω με αυτά;».
Όσο πλησίαζε η αποφοίτηση, έθεσα έναν στόχο για την καριέρα μου: να μην τρέμω κάθε πρωί πηγαίνοντας στη δουλειά, όπως όταν πήγαινα στο αμφιθέατρο. Τα χρήματα δε θα μπορούσαν ποτέ να εξισορροπήσουν αυτό το συναίσθημα.
Όταν λοιπόν αποφοίτησα, έκλεισα τα εγχειρίδια μαθηματικών μια για πάντα. Ανακάλυψα νέα πάθη, απέκτησα νέες δεξιότητες και ωρίμασα σε διαφορετικούς τομείς. Μετά από έξι χρόνια καριέρας, μπορώ να πω ότι το να είμαι άνετος με αριθμούς και δεδομένα αποδείχθηκε χρήσιμο, αλλά το πιο ανεκτίμητο είναι οι αξίες που μου προσέφεραν τα μαθηματικά – η υπομονή, η προσοχή στη λεπτομέρεια, η ταπεινότητα και η επιμονή. Αυτό ήταν το πραγματικό κέρδος.
Μετά από όλον αυτόν τον πόνο, το άγχος και τον εκνευρισμό, ίσως να ήταν καθαρτικό να βουτήξω όλα τα βιβλία μαθηματικών που είχα στην κηροζίνη και να τα κάψω. Αντιθέτως, τα κράτησα. Είναι όλα στο τελευταίο συρτάρι. Παρόλο που δεν τα έχω βγάλει ποτέ από εκεί, μου αρέσει να τα έχω πρόχειρα κοντά μου.
Για αρκετό καιρό, πίστευα ότι αυτό είναι το σύνδρομο του συλλέκτη. Πρόσφατα, όμως, μετακόμισα και οργάνωσα τη βιβλιοθήκη μου από πάνω προς τα κάτω: πρώτα τα μυθιστορήματα, μετά η αφηγηματική μυθοπλασία και στη μέση τα απομνημονεύματα. Θα ορκιζόμουν ότι άκουσα το ξύλο να τρίζει και τα ράφια να γλιστρούν προς τα εμπρός. Η βιβλιοθήκη ήταν πολύ βαριά στην κορυφή.
Χρειαζόμουν εκείνη την τελευταία σειρά από βιβλία μαθηματικών. Ήταν η άγκυρά μου. Το στήριγμά μου. Το θεμέλιο όλων όσα έμαθα, και μια γερή βάση για όσα πρόκειται να έρθουν.
Γράφει ο: Alex Korchinski
Μετάφραση: Χρήστος Κατσανδρής
Πηγή: forge.medium.com
Αναδημοσίευση από : omathimatikos.gr
Πολύ συχνά οι μαθητές και οι γονείς τους περιγράφουν ένα «αόρατο χέρι» που ανεβοκατεβάζει τις βάσεις των σχολών. Πάρα πολλοί δυσκολεύονται να κατανοήσουν ότι είναι οι ίδιοι οι μαθητές ( με την επίδοσή τους αλλά και τις επιλογές του μηχανογραφικού τους δελτίου ) αυτοί που καθορίζουν την πορεία των βάσεων.
Οι μαθητές “μπαίνουν σε σειρά” σύμφωνα με την βαθμολογία τους
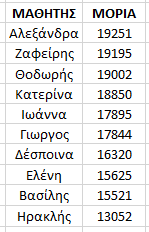και καλούνται να δηλώσουν τις σχολές που επιθυμούν με σειρά προτίμησης (μηχανογραφικό σχολών) Για λόγους απλοποίησης της διαδικασίας παρουσιάζονται μέχρι 3 επιλογές τους .
Το σύστημα/πρόγραμμα απόδοσης σχολών αρχίζει να διαβάζει τις επιλογές τους ξεκινώντας από τον μαθητή με την υψηλότερη βαθμολογία “ικανοποιώντας” τις επιθυμίες τους εφόσον αυτό είναι δυνατόν .
Ποιος το καθορίζει αυτό ? Μα το πλήθος των πρωτοετών φοιτητών που έχει δηλωθεί για κάθε σχολή ( Θυμίζω ότι στο παράδειγμά μας οι σχολές έχουν δηλώσει Α=2 , Β=3, Γ=3 )
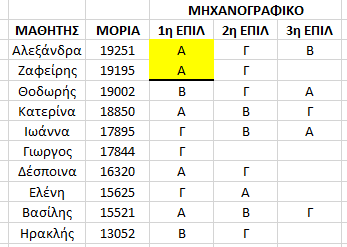Φτάνοντας στον 2ο μαθητή η σχολή Α συμπληρώνει το πληθος μαθητών που μπορεί να δεχθεί και “κλειδώνει”.
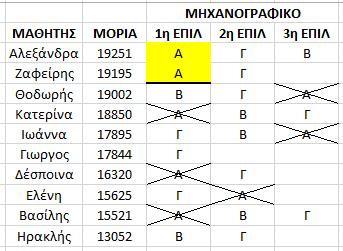Ποιός είναι ο τελευταίος που μπήκε στην σχολή ; Ο Ζαφείρης με 19195 μόρια , άρα η “βάση” της σχολής Α είναι τα 19195 μόρια του. Η σχολή Α δεν είναι πλέον διαθέσιμη για τους υπόλοιπους που ακολουθούν ενώ το σύστημα συνεχίζει στον επόμενο μαθητή με σκοπό να του ικανοποιήσει την καλύτερη ( πλέον διαθέσιμη ) επιλογή του .
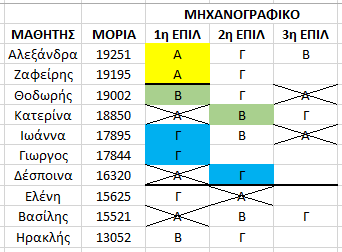Στον 7ο μαθητή ( Δέσποινα ) συμπληρώνεται το πλήθος των μαθητών που μπορεί να δεχθεί η σχολή Γ ( βάση σχολής 16320 ) και δεν είναι πλέον διαθέσιμη για τους μαθητές που ακολουθούν.
Προσέξτε όμως τι συμβαίνει τώρα !!!
Ο 8ος μαθητής ( Ελένη ) παρόλο που έχει περισσότερα μόρια από τον 9ο ( Βασίλη ) μένει εκτός σχολών γιατί οι επιλογές του ήταν περιορισμένες και είχε την ατυχία να έχει τις ίδιες επιλογές σχολών με μαθητές που ήταν καλύτεροι από αυτόν ( και “πρόλαβαν” να του τις πάρουν ). Έτσι το “σύστημα απόδοσης σχολών” προσπερνά των 8ο μαθητή ( μιας που δεν έχει σχολή να του αποδόσει ) και πηγαίνει στον επόμενο.
ο οποίος παίρνει την τελευταία διαθέσιμη θέση της καλύτερης διαθέσιμης επιλογής σχολής που έχει κάνει. ( βάση σχολής Β : 15521 )
Οι μαθητές ήταν 10 ενώ οι διαθέσιμες θέσεις ήταν 8 ( 2+3+3 ), έτσι ξέραμε από την αρχή ότι 2 μαθητές θα μείνουν εκτός σχολών . Προσέξτε όμως !!! Ένας έμεινε εκτός γιατί είχε χαμηλή βαθμολογία ( Ηρακλής ) και το σύστημα δεν έφτασε καν σε αυτόν να τον ρωτήσει ενώ ένας μαθητής ( Ελένη ) έμεινε εκτός γιατί έκανε “λάθος” στο μηχανογραφικό και επέτρεψε στο σύστημα να την προσπεράσει χωρίς να της αποδώσει μια σχολή.
Τι θα συνέβαινε εάν όλοι οι μαθητές είχαν 1000 μόρια λιγότερα ( ή 1000 μόρια περισσότερα ) επειδή τα θέματα στις πανελλήνιες ήταν πιο δύσκολα ( ή πιο εύκολα )
Μα βέβαια δεν θα υπήρχε καμία διαφορά .Το σύστημα θα κατέληγε στην ίδια αρχική κατάταξη και ακολουθώντας την ίδια πορεία θα έκανε την ίδια απόδοση σχολών.
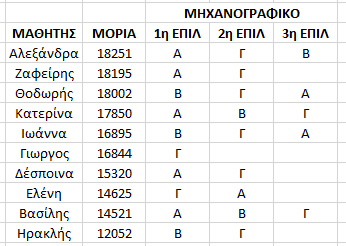Να λοιπόν γιατί ακούτε την έκφραση ότι η δυσκολία ή η ευκολία των θεμάτων δεν έχει κάποια ιδιαίτερη σημασία. ΓΙΑΤΙ ΠΟΛΥ ΑΠΛΑ ΤΑ ΘΕΜΑΤΑ ΕΙΝΑΙ ΚΟΙΝΑ ΓΙΑ ΟΛΟΥΣ !!! Μπορεί να δώσουν στρεβλή κατάταξη ( συμπιέζοντας της επιδόσεις των μαθητών σε λίγα μόρια ή σε πολλά … αλλά αυτό είναι μια άλλη ιστορία )
Ας ξανατρέξει το σύστημα/πρόγραμμα απόδοσης σχολών :
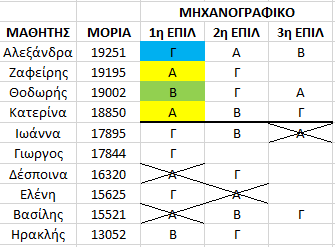Η σχολή που κλειδώνει 1η είναι πάλι η Α αλλά αυτήν την φορά αυτό συμβαίνει στον 4ο μαθητή ( Κατερίνα ) και ως βάση της χαρακτηρίζονται τα 18850 μόριά του . Η απόδοση σχολών συνεχίζει δίνοντας στους μαθητές τις καλύτερες διαθέσιμες επιλογές τους. Η επόμενη σχολή που κλειδώνει ( και δεν είναι πλέον διαθέσιμη ) είναι η σχολή Γ και ως βάση της χαρακτηρίζεται ο βαθμός του τελευταίου εισακτέου σε αυτήν ( Γιώργος / βάση σχολής Γ : 17844 )
Η απόδοση σχολών συνεχίζει – προσπερνά την Δέσποινα και την Ελένη που οι σχολές που επιθυμούσαν είναι πλέον γεμάτες – και δίνει στον Βασίλη και στον Ηρακλή ( δύο μαθητές με χαμηλότερες βαθμολογίες ) την σχολή Β που είχε κενές θέσεις . ( βάση Β : 13052 μόρια )
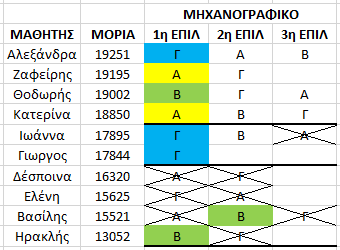Προσέξτε πως η αλλαγή σε 1 μόνο σχολή έδωσε απέδωσε διαφορετικές σχολές στους μαθητές και πως άλλαξαν οι βάσεις των σχολών . ( η μεγάλη αυτή αλλαγή έγινε γιατί ο μαθητής που άλλαξε μηχανογραφικό ήταν 1ος στην προτεραιότητα … με λίγα λόγια πειράξαμε το 1ο “τουβλάκι” στο ντόμινο … αν αλλάζαμε το μηχανογραφικό του 4ου μαθητή η αλλαγή αυτή θα επηρέαζε ΜΟΝΟ τους μαθητές που θα είχαν μικρότερη βαθμολογία από αυτόν )
Νά λοιπόν τι είναι οι πανελλήνιες εξετάσεις !!! Είναι ένας διαγωνισμός στο οποίο ο κάθε μαθητής προσπαθεί να συγκεντρώσει το καλύτερο “σκορ” ώστε να μπορέσει να διαλέξει την σχολή που επιθυμεί χωρίς να το απασχολούν οι επιλογές των άλλων ή το πλήθος των θέσεων που προκηρύσσει κάθε σχολή .
Ας δούμε πως επηρεάζεται η απόδοση σχολών στους μαθητές εάν οι θέσεις στις σχολές ήταν διαφορετικές . Ας δούμε τι θα συνέβαινε εάν η σχολή Α δέχονταν 3 μαθητές , η σχολή Β δέχονταν 2 μαθητές και η σχολή Γ δέχονταν 3 μαθητές.
Κρατώντας τις ίδιες επιδόσεις μαθητών και το ίδιο μηχανογραφικό ( όπως στο 1ο παράδειγμα ) το πρόγραμμα απόδοσης σχολών αρχίζει ξανά να σαρώνει ξεκινώντας πάλι από τον μαθητή με την μεγαλύτερη βαθμολογία .
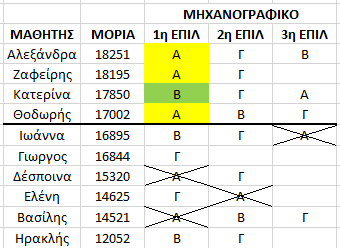Βάση σχολής Α : 17002
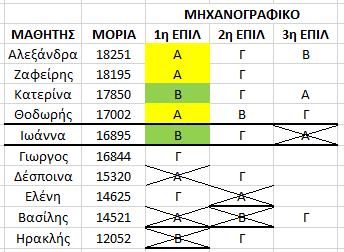Βάση σχολής Β : 16895
Βάση σχολής Γ : 14625
Συμπέρασμα ( αντί επιλόγου )
Είναι φανερό ότι ο κάθε μαθητής δεν μπορεί να γνωρίζει ούτε το πλήθος των μαθητών που έχουν καλύτερη βαθμολογία από αυτόν αλλά ( κυρίως ) ούτε ποιές είναι οι επιλογές σχολών που έχουν κάνει αυτοί οι μαθητές , Για αυτόν τον λόγο πρέπει να κάνει μηχανογραφικό σαν να έχει το απόλυτο πλεονέκτημα δηλαδή 20000 μόρια. Δηλώνουμε όλες τις σχολές που μας ενδιαφέρουν σε όλες τις πόλεις που η οικογένεια μας μπορεί να υποστηρίξει οικονομικά τις σπουδές μας . Με αυτόν τον τρόπο ελαχιστοποιείται η πιθανότητα δυσάρεστων εκπλήξεων τον Αύγουστο.
Επιμέλεια άρθρου: Αντώνης Μπαλτζόπουλος-Χημικός
Πρόσφατα σχόλια