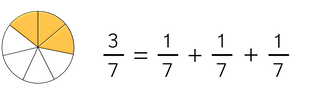Για να μετατρέψουμε έναν δεκαδικό αριθμό σε κλάσμα:
- Γράφουμε ολόκληρο τον αριθμό, χωρίς την υποδιαστολή, στη θέση του αριθμητή.
- Στη θέση του παρονομαστή γράφουμε τον αριθμό 1, με τόσα μηδενικά όσα ήταν τα δεκαδικά ψηφία του αριθμού.
Για να μετατρέψουμε ένα δεκαδικό κλάσμα σε δεκαδικό αριθμό:
- Γράφουμε μόνο τον αριθμητή του.
- Χωρίζουμε με υποδιαστολή, από τα δεξιά προς τ’ αριστερά, τόσα δεκαδικά ψηφία όσα μηδενικά έχει ο παρονομαστής του.

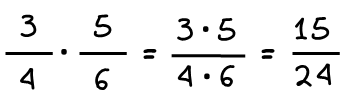
ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΚΛΑΣΜΑΤΩΝ
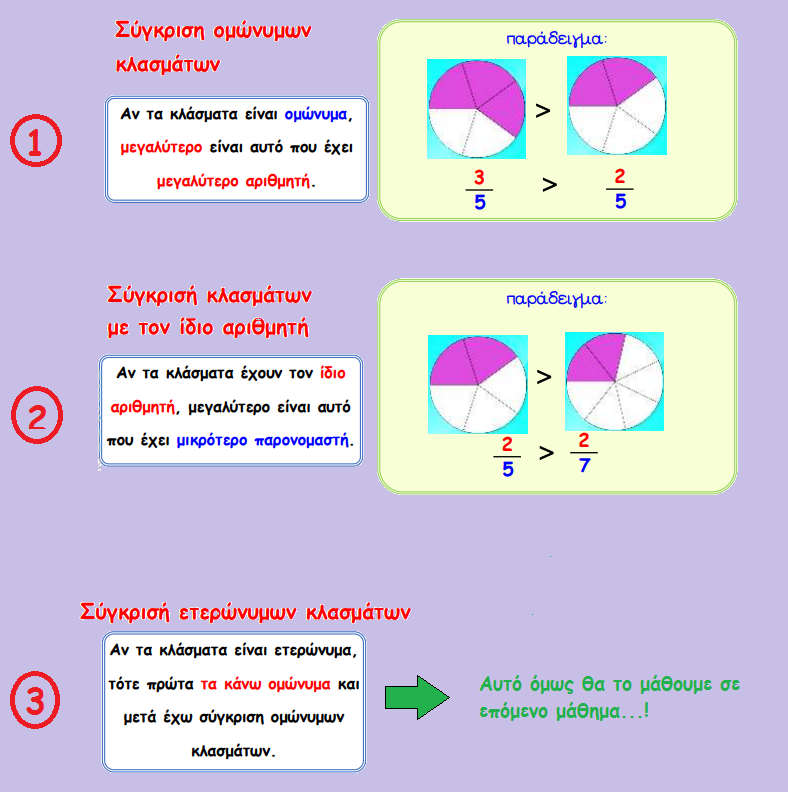
ΣΥΓΚΡΙΣΗ ΚΛΑΣΜΑΤΩΝ
Οπτικοποίηση και σύγκριση των κλασμάτων που δημιουργούμε.
numerator – αλλάζεις τον αριθμητή , Denominator – αλλάζεις τον παρονομαστή
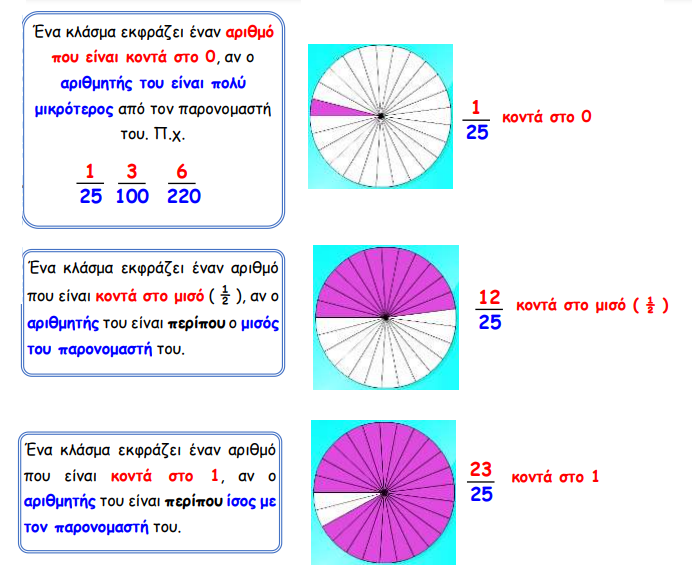
ΙΣΟΔΥΝΑΜΙΑ ΚΛΑΣΜΑΤΩΝ
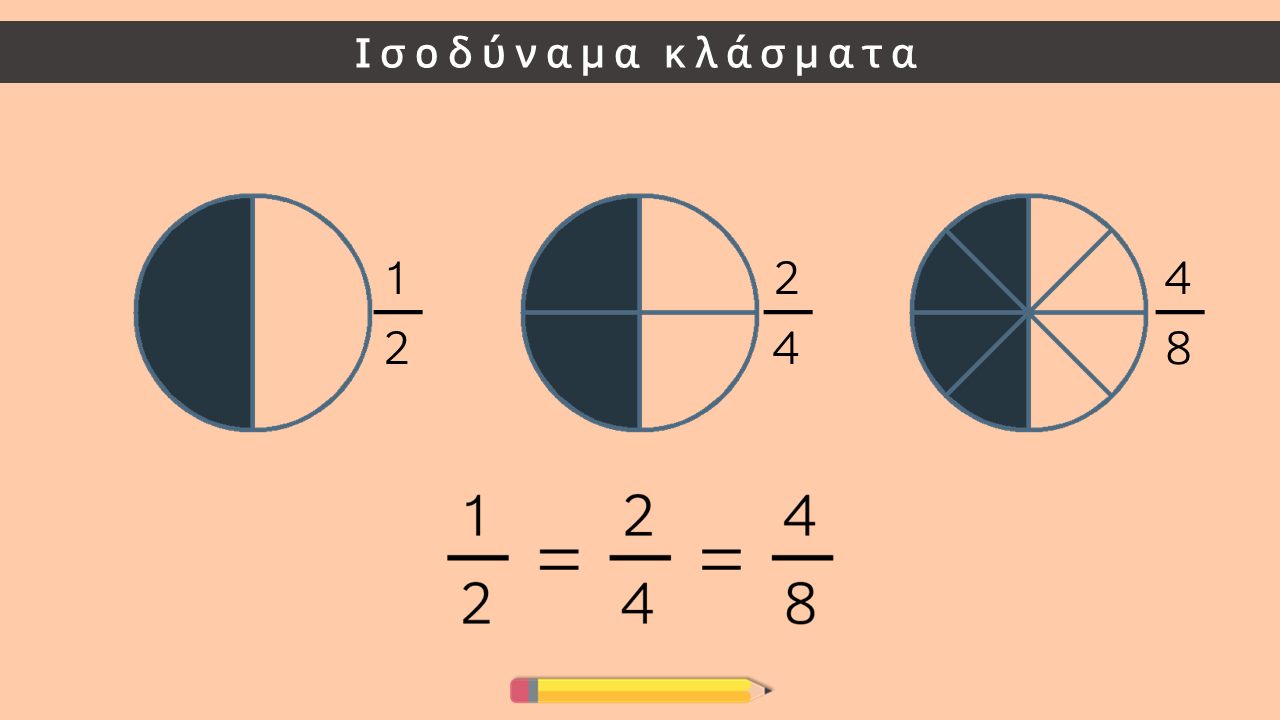
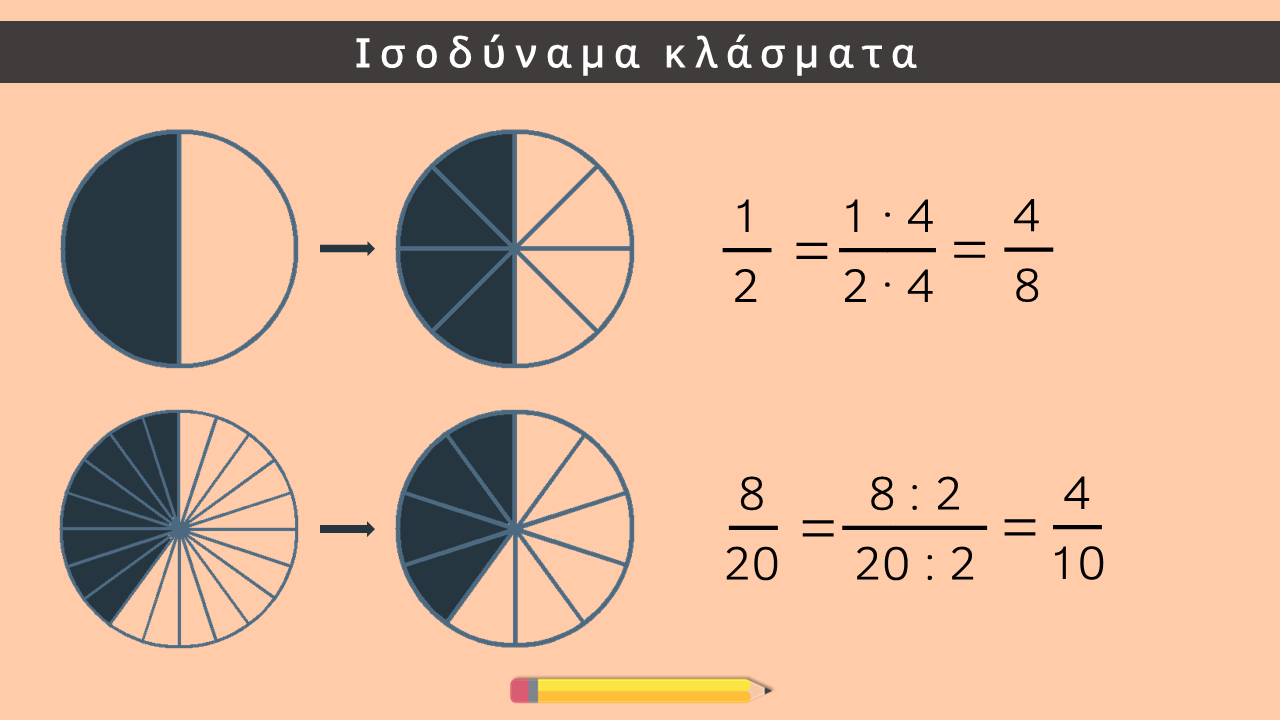
Ισοδύναμα κλάσματα
- Δύο ή περισσότερα κλάσματα που έχουν διαφορετικούς όρους, δηλαδή διαφορετικό αριθμητή & παρονομαστή, αλλά εκφράζουν την ίδια ποσότητα, λέγονται ισοδύναμα.
- Δύο ή περισσότερα κλάσματα όταν έχουν ίσους παρονομαστές λέγονται ομώνυμα ενώ αν έχουν διαφορετικούς λέγονται ετερώνυμα. Και οι δύο μαζί (αριθμητής και παρονομαστής) λέγονται όροι του κλάσματος.
και τους δύο όρους ενός κλάσματος με τον ίδιο αριθμό.
|
|

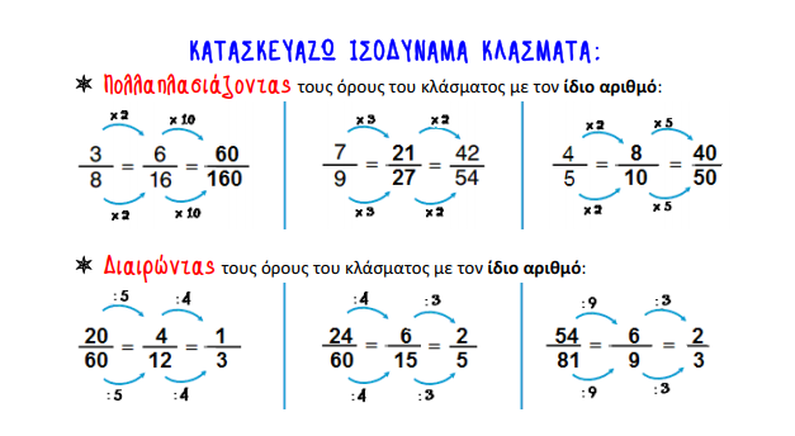
Δημιουργώ ισοδύναμα κλάσματα πολλαπλασιάζοντας ή διαιρώντας και τους δύο όρους ενός κλάσματος με τον ίδιο αριθμό.
Όταν πολλαπλασιάζω και τους δύο όρους του κλάσματος, δημιουργώ ένα ισοδύναμο κλάσμα με μεγαλύτερους όρους.
Όταν διαιρώ και τους δύο όρους του κλάσματος με τον ίδιο αριθμό, δημιουργώ ένα ισοδύναμο κλάσμα με μικρότερους όρους. Η διαδικασία αυτή ονομάζεται απλοποίηση (το κλάσμα γίνεται πιο απλό).

Το κλάσμα ως πηλίκο διαίρεσης
- Κάθε κλάσμα είναι ίσο με το πηλίκο μιας διαίρεση: (αριθμητής) : (παρονομαστή)
- Αντίστροφα κάθε διαίρεση μπορούμε να την εκφράσουμε και ως κλάσμα.
- Κάθε κλάσμα μπορεί να εκφραστεί ως δεκαδικός αν κάνουμε τη διαίρεση.
- Αν η διαίρεση είναι ατελής σταματάμε όπου μας χρειάζεται.
- Κάθε δεκαδικός μπορεί να μετατραπεί σε κλάσμα.


ΜΕΤΑΤΡΟΠΗ ΚΛΑΣΜΑΤΟΣ ΣΕ ΜΕΙΚΤΟ ΑΡΙΘΜΟ
8/3= 3/3 + 3/3 + 2/3=1 + 1+ 2/3=2+2/3
20/8= 8/8 + 8/8+ 4/8= 1 + 1 + 4/8= 2+4/8
25/3= 3/3 + 3/3 + 3/3 + 3/3 + 3/3 + 3/3 + 3/3 + 3/3 + 1/3=
1+1+1+1+1+1+1+1+1/3=8+1/3
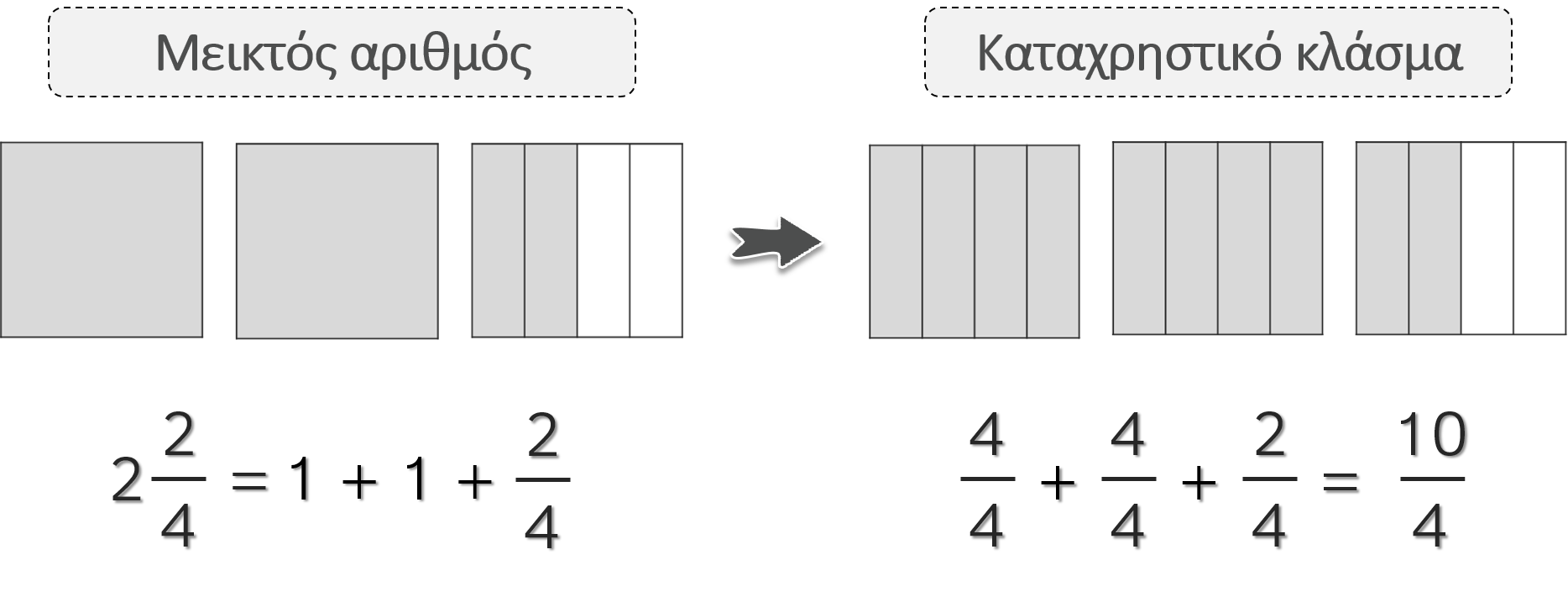
ΜΕΤΑΤΡΟΠΗ ΜΕΙΚΤΟΥ ΑΡΙΘΜΟΥ ΣΕ ΚΛΑΣΜΑ
|

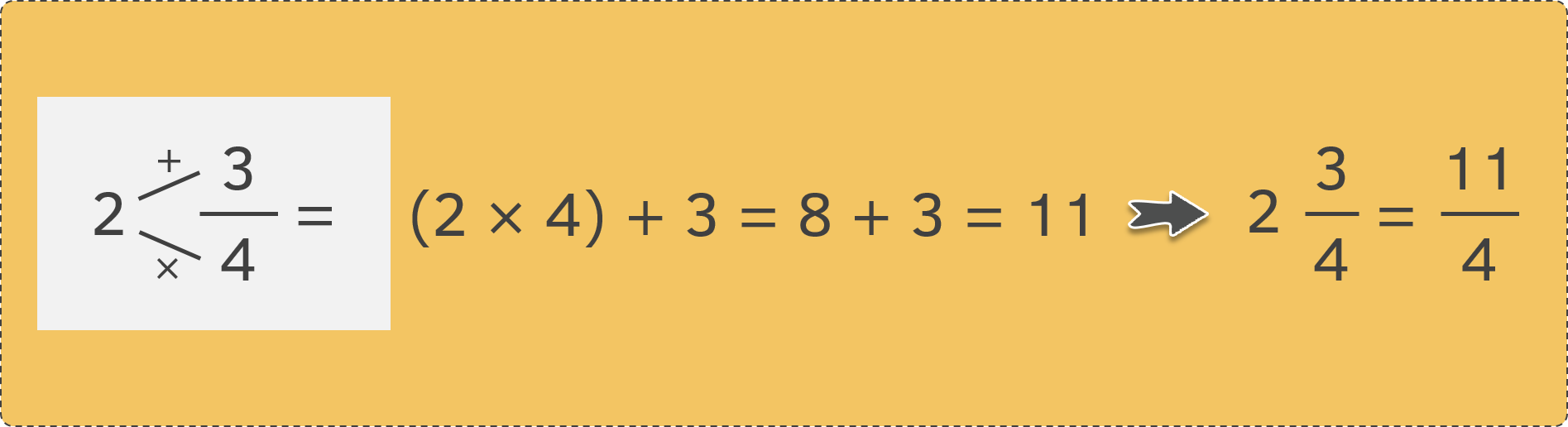
- Πολλαπλασιάζουμε τον ακέραιο του μεικτού με τον παρονομαστή του κλάσματός του.
- Στο γινόμενο που προκύπτει προσθέτουμε τον αριθμητή του μεικτού αριθμού.
- Το αποτέλεσμα αποτελεί τον αριθμητή του νέου κλάσματος, ενώ παρονομαστής παραμένει ο ίδιος.
Τι είναι κλάσμα;


|
Κλάσμα, ονομάζουμε το μέρος μιας ακέραιης μονάδας η οποία έχει χωριστεί σε ίσα μέρη.
Τα κλάσματα γράφονται με δύο αριθμούς (ο ένας κάτω από τον άλλο), που χωρίζονται με μία γραμμή, την κλασματική γραμμή. Όροι του κλάσματος
|
|
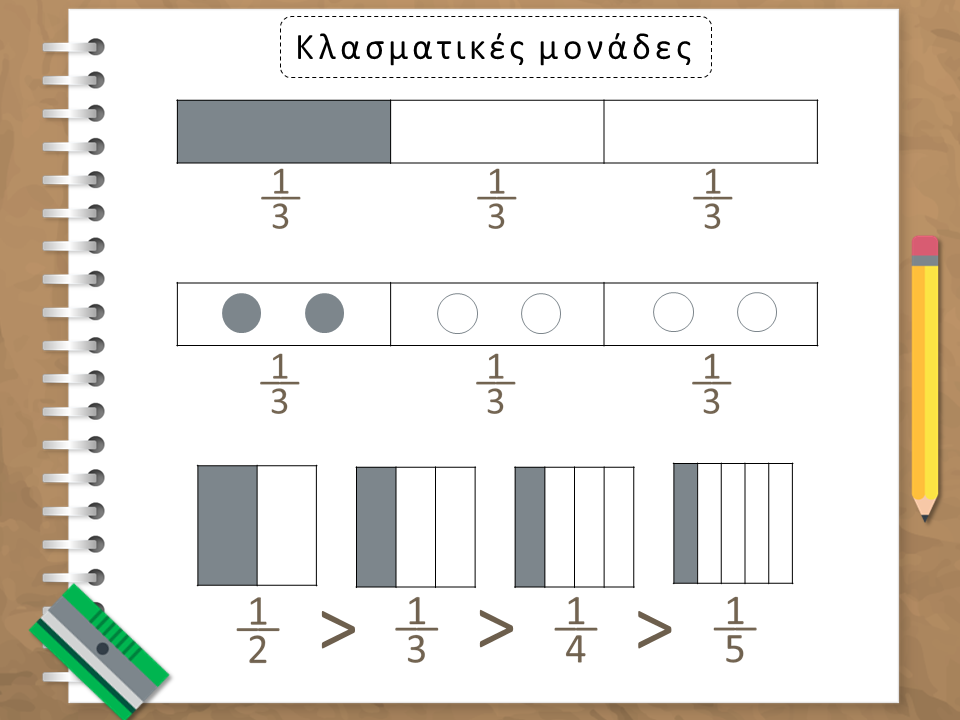
Κλασματική μονάδα
|
Κλασματική μονάδα είναι το ένα από τα ίσα μέρη, στα οποία χωρίζουμε μια ακέραιη μονάδα.
|
|
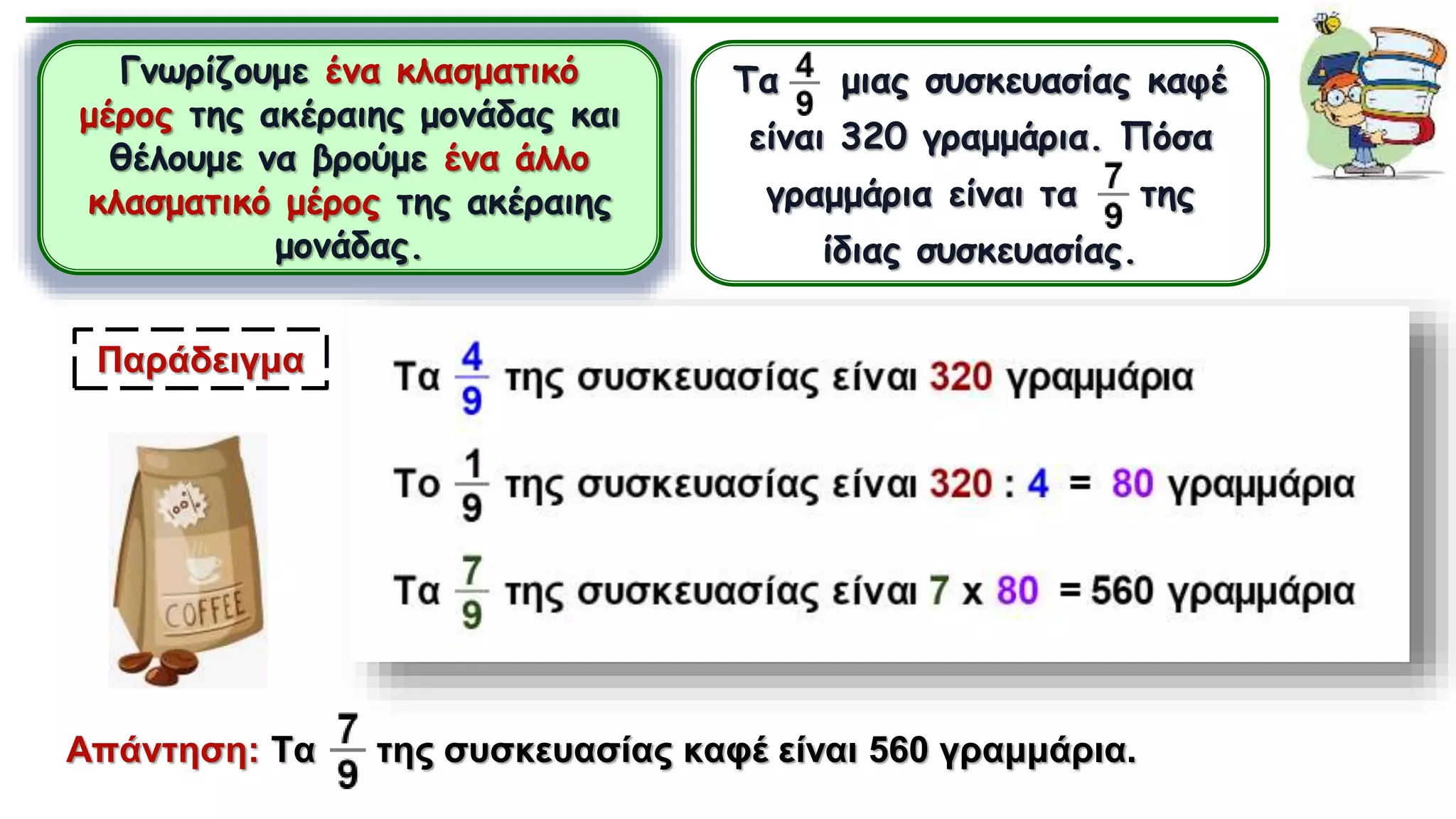
- Όταν γνωρίζουμε την τιμή της μιας κλασματικής μονάδας, μπορούμε να υπολογίσουμε την αξία ολόκληρης της ακέραιης μονάδας. Π.χ. Αν το 1/4 των μαθητών της τάξης είναι 5 μαθητές, τότε ολόκληρη η τάξη έχει 4 Χ 5 = 20
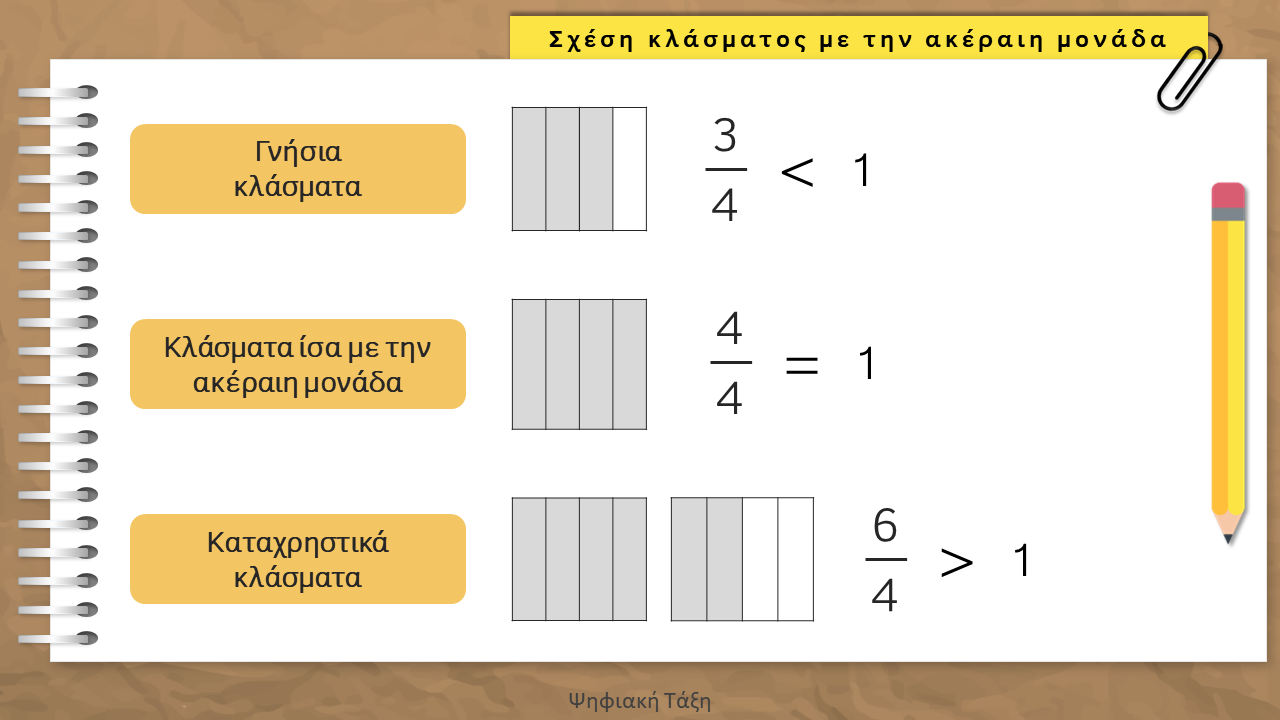
Γνήσια κλάσματα λέγονται τα κλάσματα που είναι μικρότερα από την ακέραια μονάδα. Έχουν, δηλαδή, τον αριθμητή μικρότερο από τον παρονομαστή.
Κλάσματα ίσα με την ακέραια μονάδα είναι εκείνα που έχουν τον αριθμητή ίσο με τον παρονομαστή.
Καταχρηστικά λέγονται τα κλάσματα που είναι μεγαλύτερα από την ακέραια μονάδα. Έχουν, δηλαδή, τον αριθμητή μεγαλύτερο από τον παρονομαστή.
Η ΔΙΑΙΡΕΣΗ ΣΤΟΥΣ ΦΥΣΙΚΟΥΣ ΑΡΙΘΜΟΥΣ
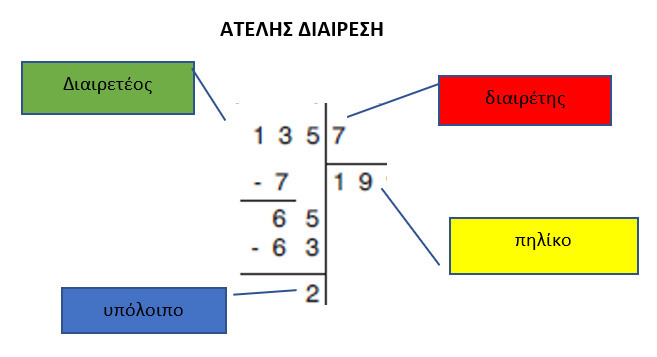

Διαβάζω τα παρακάτω και θυμάμαι …
-
Τέλεια διαίρεση λέγεται η διαίρεση στην οποία το υπόλοιπο είναι 0. Όταν το υπόλοιπο δεν είναι 0, η διαίρεση λέγεται ατελής.
-
Η τέλεια διαίρεση είναι αντίστροφη πράξη του πολλαπλασιασμού. Σε μια τέλεια διαίρεση ο διαιρετέος είναι ίσος με το γινόμενο του διαιρέτη επί το πηλίκο.
-
Σε κάθε διαίρεση ο διαιρετέος είναι ίσος με το γινόμενο του διαιρέτη επί το πηλίκο συν το υπόλοιπο.
Παράδειγμα : 30 : 7 = 4 υπολ. : 2 30= 4 * 7 + 2
-
Ένας αριθμός, αν διαιρεθεί με το 1 δίνει πηλίκο τον εαυτό του (και υπόλοιπο 0).
-
Ένας αριθμός, αν διαιρεθεί με τον εαυτό του, δίνει πηλίκο 1 (και υπόλοιπο 0).
-
Το 0 με όποιον αριθμό και αν διαιρεθεί δίνει πηλίκο 0.
-
Σε μια διαίρεση, αν πολλαπλασιάσουμε ή διαιρέσουμε και τους δύο όρους με τον ίδιο αριθμό, το πηλίκο δεν αλλάζει.
Παράδειγμα : 20 : 5 = 4 ( 20 * 3 ) : ( 5 * 3 ) = 60 : 15 = 4
Έχουμε δυο ειδών διαιρέσεις:
-
Τη διαίρεση μερισμού. Όταν ξέρουμε την τιμή των πολλών μονάδων και ζητάμε την τιμή της μιας μονάδας.
Π.χ. Οι πέντε σοκολάτες κοστίζουν 10 €. Πόσο κοστίζει η μία;
-
Τη διαίρεση μέτρησης. Όταν ξέρουμε και την τιμή των πολλών μονάδων και την τιμή της μιας μονάδας και δεν ξέρουμε πόσες είναι αυτές οι πολλές μονάδες.
Π.χ. Αν έχω 12 κιλά μέλι και γεμίσω βάζα των 2 κιλών το καθένα. Πόσα βάζα χρησιμοποίησα;









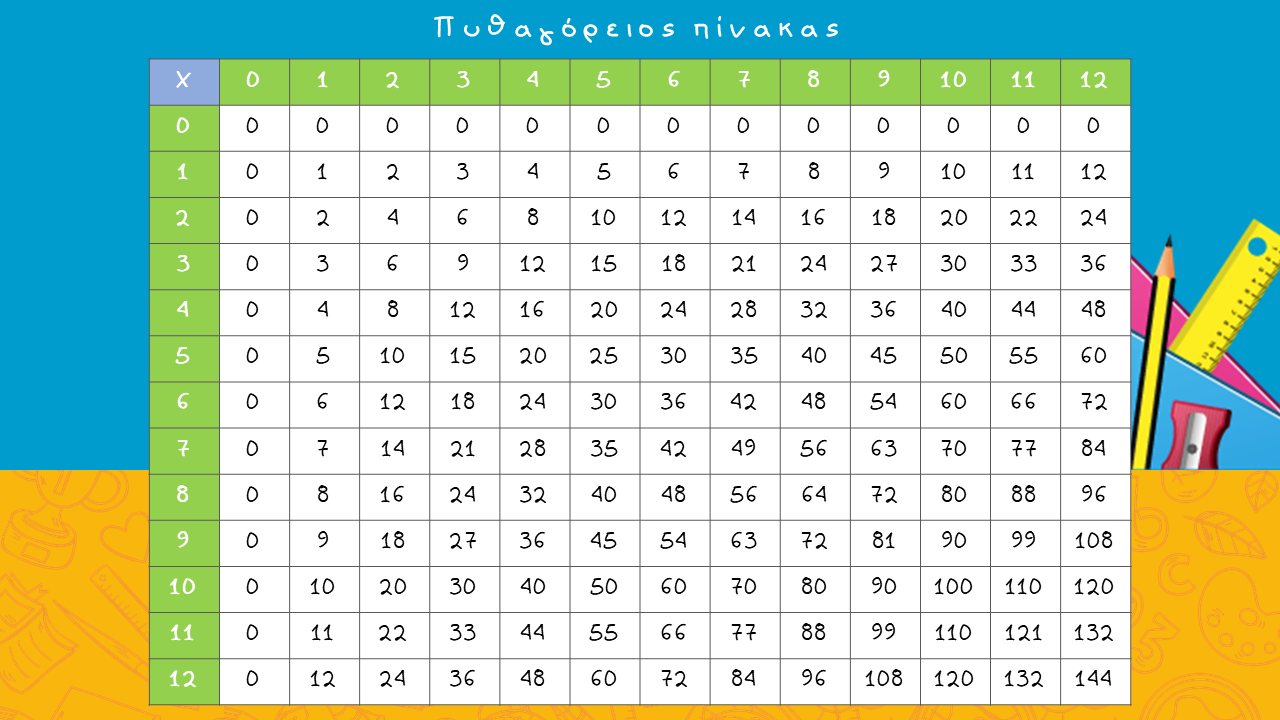
Ο Πυθαγόρας και ο Πυθαγόρειος πίνακας
|
Στην αρχαία Ελλάδα ζούσε ο Πυθαγόρας, μεγάλος φιλόσοφος και μαθηματικός. Γεννήθηκε σε χρονολογία που δεν μας είναι γνωστή, αλλά που εικάζεται πως είναι το 570 π.Χ. και ως επικρατέστερος τόπος γεννήσεως φέρεται η νήσος Σάμος. Είχε εφεύρει έναν «πίνακα», όπως τον έλεγε, που διευκόλυνε τους πολλαπλασιασμούς, οι οποίοι έως τότε γίνονταν με το μυαλό ή απλούστερα με πετραδάκια.
|


Στρογγυλοποίηση στους φυσικούς αριθμούς

- Βρίσκουμε το ψηφίο στο οποίο θέλουμε να γίνει η στρογγυλοποίηση.
- Κοιτάζουμε το ψηφίο που βρίσκεται δεξιά από αυτό στο οποίο θα κάνουμε στρογγυλοποίηση.
- Αν είναι 0 ή 1 ή 2 ή 3 ή 4 το ψηφίο της στρογγυλοποίησης θα μείνει το ίδιο ενώ όλα όσα βρίσκονται δεξιά του θα γίνουν 0.
- Αν είναι 5 ή 6 ή 7 ή 8 ή 9, τότε το ψηφίο της στρογγυλοποίησης αυξάνεται κατά 1 και όλα τα ψηφία που βρίσκονται δεξιά του θα γίνουν 0.
ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ
Οι αριθμοί 0, 1, 2, 3, …, 98, 99, 100, …, ονομάζονται φυσικοί αριθμοί.
- Καθένας από τους φυσικούς αριθμούς εκφράζει ολόκληρες μονάδες, εκτός από το 0.
- Γράφουμε τους φυσικούς αριθμούς χρησιμοποιώντας τα δέκα ψηφία: 0, 1, 2, 3, 4, 5, 6, 7, 8 και 9.
- Κάθε φυσικός αριθμός έχει έναν επόμενο και έναν προηγούμενο φυσικό αριθμό, εκτός από τον αριθμό 0, ο οποίος έχει μόνον επόμενο, τον αριθμό 1.
- Ο αριθμός 0 είναι ο μικρότερος φυσικός αριθμός.
- Μεγαλύτερος φυσικός αριθμός δεν υπάρχει γιατί για κάθε φυσικό αριθμό υπάρχει ο επόμενός του.
1. Κατανόηση του Προβλήματος
Πρώτα απ’ όλα, διαβάστε το πρόβλημα προσεκτικά. Διαβάστε το μία, δύο, ακόμα και τρεις φορές, αν χρειάζεται.
- Τι μου ζητάει το πρόβλημα; Ποια είναι η τελική ερώτηση;
- Ποια στοιχεία μου δίνει; Ποιοι αριθμοί και ποιες πληροφορίες είναι σημαντικές; Μερικές φορές, υπάρχουν και πληροφορίες που δεν χρειάζονται, οπότε προσέξτε!
- Μπορώ να το ζωγραφίσω; Μια ζωγραφιά ή ένα διάγραμμα μπορεί να σας βοηθήσει να δείτε το πρόβλημα πιο καθαρά.
2. Σχεδιασμός της Λύσης
Τώρα που καταλάβατε τι ζητάει το πρόβλημα, σκεφτείτε πώς θα το λύσετε.
- Ποια πράξη θα κάνω; Είναι πρόσθεση, αφαίρεση, πολλαπλασιασμός ή διαίρεση; Ίσως χρειαστεί να κάνετε περισσότερες από μία πράξεις.
- Ποια είναι η σειρά των βημάτων; Οργανώστε τις πράξεις σας με τη σωστή σειρά. Σκεφτείτε “Πρώτα θα κάνω αυτό, μετά εκείνο…”.
3. Εκτέλεση της Λύσης
Εφαρμόστε το σχέδιό σας και κάντε τις πράξεις.
- Κάντε τους υπολογισμούς με προσοχή. Μπορείτε να χρησιμοποιήσετε πρόχειρο για να κάνετε τις πράξεις πιο εύκολα.
- Γράψτε τα βήματά σας. Είναι σημαντικό να φαίνεται πώς φτάσατε στο αποτέλεσμα.
4. Έλεγχος της Απάντησης
Αφού βρήκατε το αποτέλεσμα, μην βιαστείτε! Είναι πολύ σημαντικό να ελέγξετε τη δουλειά σας.
- Είναι λογική η απάντηση; Για παράδειγμα, αν ένα πρόβλημα λέει ότι η Μαρία είχε 10 ευρώ και αγόρασε κάτι με 3 ευρώ, η απάντηση “13 ευρώ” δεν είναι λογική.
- Ξανακάντε τις πράξεις. Μπορείτε να ξανακάνετε τους υπολογισμούς για να βεβαιωθείτε ότι δεν κάνατε κάποιο λάθος.
- Απαντήστε στην ερώτηση. Στο τέλος, γράψτε την τελική σας απάντηση με μια ολοκληρωμένη πρόταση.
Ακολουθώντας αυτά τα βήματα, κάθε μαθηματικό πρόβλημα γίνεται πιο εύκολο και η λύση του είναι πιο κοντά! 🚀