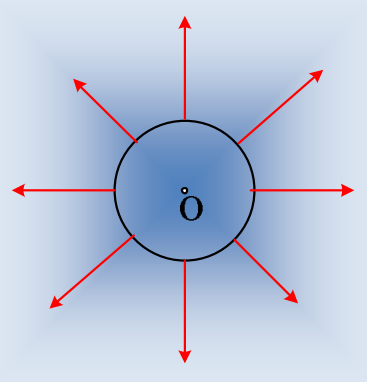
Το ηλεκτρικό πεδίο μιας αγώγιμης φορτισμένης σφαίρας περιορίζεται στο εξωτερικό της και είναι όμοιο με το ηλεκτρικό πεδίο σημειακού φορτίου, το οποίο θα βρισκόταν στο κέντρο της. Αν δηλαδή έχουμε μια μεταλλική σφαίρα με θετικό φορτίο Q, η μορφή του ηλεκτρικού της πεδίου είναι αυτό που παριστάνεται με τις δυναμικές γραμμές του διπλανού σχήματος.
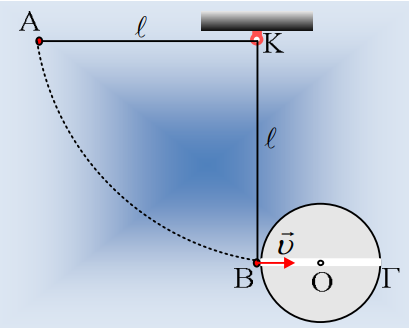Έστω ότι έχουμε μια ακλόνητη μεταλλική σφαίρα ακτίνας R=0,1m η οποία είναι φορτισμένη με φορτίο Q=1μC. Ένα μικρό μεταλλικό σφαιρίδιο μάζας m=10g είναι δεμένο στο άκρο μονωτικού νήματος μήκους l=0,3m, το άλλο άκρο του οποίου είναι σταθερά δεμένο σε σημείο Κ, έχοντας φορτίο q=-(5/24)μC. Φέρνουμε το σφαιρίδιο στη θέση Α με το νήμα τεντωμένο σε οριζόντια θέση και το αφήνουμε να κινηθεί, οπότε μετά από λίγο φτάνει στη θέση Β στην επιφάνεια της σφαίρας, με το νήμα κατακόρυφο. Στη θέση αυτή κόβεται το νήμα και το σφαιρίδιο έχοντας ταχύτητα υ, συνεχίζει την κίνησή του στο εσωτερικό μιας μικρής οριζόντιας σήραγγας, η οποία αφού περάσει από το κέντρο Ο της σφαίρας καταλήγει στο σημείο Γ. Η κίνηση εντός της σήραγγας πραγματοποιείται, χωρίς τριβές.
- Να υπολογίσετε τα έργα των δυνάμεων που ασκούνται στο σφαιρίδιο κατά την κίνησή του από τη θέση Α στη θέση Β.
- Να βρεθεί το μέτρο της ταχύτητας υ.
- Με ποια ταχύτητα περνά το σφαιρίδιο από το κέντρο Ο της σφαίρας και με ποια ταχύτητα εξέρχεται από το άκρο Γ της σήραγγας;
- Να υπολογιστεί η δυναμική ενέργεια του σφαιριδίου, η οφειλόμενη στο φορτίο που φέρει, τη στιγμή που διέρχεται από το κέντρο Ο της σφαίρας.
Δίνονται g=10m/s2 και Κ=9∙109Νm2/C2.
ή
 |
Κίνηση σε σήραγγα… |
 |
Κίνηση σε σήραγγα… |