Θα ανέβει ο Καλόγερος;
Ένα θέμα από τον διαγωνισμό ΦΥΣΙΚΗΣ 2008
Μπείτε να δείτε και όλες τις απαντήσεις:
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤ. Γ
Ένας κύλινδρος μάζας m=50kg και ακτίνας R=0,4m ηρεμεί σε τραχύ οριζόντιο δρόμο. Για t=0 σπρώχνεται από ένα παιδί με μια σταθερή οριζόντια δύναμη F=60Ν σε ένα σημείο που απέχει κατακόρυφη απόσταση h=0,5m από το έδαφος, μέχρι τη στιγμή t=10s, όπου φτάνει σε λείο κεκλιμένο επίπεδο, στο οποίο συνεχίζει την κίνησή του, χωρίς να σπρώχνεται από το παιδί. Αν στον οριζόντιο δρόμο ο κύλινδρος κυλίεται χωρίς να ολισθαίνει, γύρω από τον άξονά του για τον οποίο Ι= 1/2 mR2 και g=10m/s2, ζητούνται:
α) Η επιτάχυνση του άξονα του κυλίνδρου.
β) Ο ρυθμός μεταβολής της στροφορμής του κυλίνδρου για t1=5s.
γ) Η κινητική ενέργεια του κυλίνδρου τη στιγμή που φτάνει στην κορυφή του κεκλιμένου επιπέδου.
δ) Την ταχύτητα του άξονα του κυλίνδρου, όταν κατέλθει κατακόρυφα κατά h1=2,2m κατά την κίνησή του στο κεκλιμένο επίπεδο.
Μπορείτε να δείτε όλο το διαγώνισμα από ΕΔΩ.
ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2008
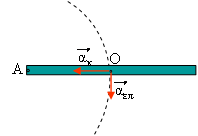
Το σώμα που φαίνεται στο διπλανό σχήμα, αφήνεται πάνω από το οριζόντιο δάπεδο με το οποίο δεν παρουσιάζει τριβή. Στο σχήμα φαίνεται και το κέντρο μάζας Κ του σώματος το οποίο τη στιγμή που αφήνεται το σώμα βρίσκεται σε ύψος h. Αν η κρούση του σώματος με το δάπεδο είναι ελαστική και η αντίσταση του αέρα είναι αμελητέα, ποια από τις παρακάτω προτάσεις είναι σωστή;
α. Το κέντρο μάζας του σώματος μετά την κρούση θα εκτελέσει πλάγια βολή προς τα δεξιά και θα φτάσει σε μικρότερο ύψος από το ύψος h από το οποίο αφέθηκε.
β. Το κέντρο μάζας του σώματος μετά την κρούση θα κινηθεί κατακόρυφα αλλά θα φτάσει σε μικρότερο ύψος από το ύψος h από το οποίο αφέθηκε.
γ. Το κέντρο μάζας του σώματος μετά την κρούση θα εκτελέσει πλάγια βολή προς τα αριστερά και θα φτάσει σε μικρότερο ύψος από το ύψος h από το οποίο αφέθηκε.
δ. Το κέντρο μάζας του σώματος μετά την κρούση θα κινηθεί κατακόρυφα και θα φτάσει σε ίδιο ύψος h από το οποίο αφέθηκε.
ε. Το κέντρο μάζας του σώματος μετά την κρούση θα εκτελέσει πλάγια βολή προς τα δεξιά και θα φτάσει στο ίδιο ύψος h από το οποίο αφέθηκε.
στ. Το κέντρο μάζας του σώματος μετά την κρούση θα εκτελέσει πλάγια βολή προς τα αριστερά και θα φτάσει στο ίδιο ύψος h από το οποίο αφέθηκε.
Να δικαιολογήσετε πλήρως την απάντησή σας.
Μπορείτε να δείτε τα θέματα και των τριών τάξεων:
Μπείτε να δείτε και όλες τις απαντήσεις:
- Μπορείτε να δείτε και μια προσομοίωση με το interactive Physics για το θέμα αυτό, από τον συνάδελφο Σαράντο Οικονομίδη
Κίνηση κυλίνδρου και τριβή 1.
Ένας κύλινδρος μάζας m και ακτίνας R ηρεμεί σε οριζόντιο επίπεδο. Σε μια στιγμή t=0 ασκείται στον άξονά του μια σταθερή οριζόντια δύναμη F, όπως στο σχήμα. Χαρακτηρίστε σαν σωστές ή λαθεμένες τις παρακάτω προτάσεις.
α) Αν το επίπεδο είναι λείο τότε ο κύλινδρος θα εκτελέσει μόνο μεταφορική κίνηση.
β) Αν υπάρχει τριβή, αυτή θα έχει φορά προς τα αριστερά.
γ) Υπεύθυνη για την περιστροφή του κυλίνδρου είναι η ασκούμενη τριβή.
δ) Η ασκούμενη τριβή είναι στατική και υπολογίζεται από την εξίσωση Τ=μsmg.
ε) Αν η τριβή είναι στατική, τότε ο κύλινδρος θα κυλίεται χωρίς να ολισθαίνει.
στ) Αν ο κύλινδρος ολισθαίνει ή όχι εξαρτάται από το μέτρο της δύναμης F.
Κίνηση κυλίνδρου και τριβή.
Ένας κύλινδρος μάζας m και ακτίνας R ηρεμεί σε οριζόντιο επίπεδο. Σε μια στιγμή t=0 ασκείται στον άξονά του μια σταθερή οριζόντια δύναμη F, όπως στο σχήμα, με αποτέλεσμα ο κύλινδρος να αρχίσει να κυλίεται χωρίς να ολισθαίνει. Ποια πρόταση είναι σωστή.
α) Το επίπεδο δεν είναι λείο και στον κύλινδρο ασκείται στατική τριβή με φορά προς τα αριστερά.
β) Το επίπεδο είναι λείο.
γ) Η μεταφορική κίνηση του σώματος είναι ευθύγραμμη ομαλή.
δ) Η μεταφορική κίνηση του σώματος είναι ευθύγραμμη ομαλά επιταχυνόμενη με επιτάχυνση που υπολογίζεται από τη σχέση F=macm.
Άνοδος κυλίνδρου σε κεκλιμένο επίπεδο.
Ένας κύλινδρος μάζας 30kg και ακτίνας R=0,4m αρχίζει να ανεβαίνει σε κεκλιμένο επίπεδο κλίσεως θ =30°. Ο κύλινδρος κυλίεται χωρίς να ολισθαίνει, έχοντας αρχική ταχύτητα υ0=10m/s. Μετά από μετατόπιση κατά x=15m, ο άξονας του κυλίνδρου έχει ταχύτητα υ1.
i) Πόση επιβράδυνση έχει ο άξονας του κυλίνδρου;
ii) Βρείτε την τριβή που ασκείται στον κύλινδρο.
iii) Πόση είναι η ταχύτητα υ1;
Δίνεται η ροπή αδράνειας του κυλίνδρου ως προς τον άξονα περιστροφής του Ι= 1/2mR2 και g=10m/s2.
Δυναμική ράβδου και δύναμη από τον άξονα περιστροφής.
Μια ομογενής δοκός μήκους l=4m και μάζας Μ=12kg μπορεί να στρέφεται γύρω από σταθερό οριζόντιο άξονα, ο οποίος διέρχεται από το ένα της άκρο Α και ισορροπεί οριζόντια με την βοήθεια κατακόρυφου νήματος, το οποίο είναι δεμένο στο άλλο της άκρο Β.
i) Βρείτε τη δύναμη που ασκείται στη δοκό από τον άξονα.
ii) Σε μια στιγμή κόβουμε το νήμα. Αμέσως μετά το κόψιμο του νήματος:
Βρείτε τη γωνιακή επιτάχυνση που αποκτά η δοκός
Πόση δύναμη ασκεί ο άξονας στη δοκό;
Δίνεται η ροπή αδράνειας της δοκού ως προς τον άξονα περιστροφής Ι= 1/3 Μl2 και g=10m/s2.
Κίνηση γιο – γιο.
Γύρω από έναν ομογενή κύλινδρο τυλίγουμε ένα αβαρές νήμα. Τραβάμε το νήμα ασκώντας στο άκρο του Α σταθερή κατακόρυφη δύναμη F, ενώ ταυτόχρονα αφήνουμε τον κύλινδρο να κινηθεί. Αν ως προς τον άξονα του κυλίνδρου Ι= 1/2 mR2.
i) Αν F=mg, τότε:
α) Ο κύλινδρος εκτελεί σύνθετη κίνηση.
β) Το σημείο Α παραμένει ακίνητο.
γ) Το σημείο Α κινείται προς τα πάνω με επιτάχυνση a=2F/m.
δ) Ο κύλινδρος κινείται προς τα πάνω με επιτάχυνση a=2F/m.
ii) Αν F=mg/2 ποια πρόταση είναι λάθος;
α) Ο κύλινδρος εκτελεί σύνθετη κίνηση. Ευθύγραμμη ομαλά επιταχυνόμενη με φορά προς τα κάτω και στροφική ομαλά επιταχυνόμενη.
β) Η επιτάχυνση του άξονα του κυλίνδρου έχει μέτρο g/2 και φορά προς τα κάτω.
γ) Η γωνιακή επιτάχυνση του κυλίνδρου είναι αντιστρόφως ανάλογη της ακτίνας του.
δ) Η επιτάχυνση του σημείου Α έχει μέτρο g/2 και φορά προς τα κάτω.
iii) Αν F=mg/2 και ο κύλινδρος μετατοπισθεί κατακόρυφα κατά h, τότε η κινητική ενέργεια του κυλίνδρου θα είναι ίση:
α) με το έργο του βάρους.
β) με τη μείωση της δυναμικής ενέργειας του κυλίνδρου.
γ) Με 2mgh
δ) Με 1,5mgh.
Κύλινδρος σε μη λείο οριζόντιο επίπεδο.
Γύρω από έναν ομογενή κύλινδρο τυλίγουμε ένα αβαρές νήμα και κατόπιν τον τοποθετούμε σε μη λείο οριζόντιο επίπεδο. Τραβώντας το νήμα για t=0 ασκούμε πάνω του οριζόντια δύναμη F, όπως στο σχήμα. Αν ως προς τον άξονα του κυλίνδρου Ι= 1/2 mR2.
i) Ο κύλινδρος θα εκτελέσει μόνο μεταφορική κίνηση ομαλά επιταχυνόμενη κίνηση.
ii) Η ασκούμενη τριβή έχει φορά προς τα αριστερά.
iii) Το σημείο Α έχει επιτάχυνση προς τα αριστερά.
iv) Για την επιτάχυνση του άξονα του κυλίνδρου ισχύει acm> F/m.
Κύλινδρος σε λείο οριζόντιο επίπεδο.
Γύρω από έναν ομογενή κύλινδρο τυλίγουμε ένα αβαρές νήμα και κατόπιν τον τοποθετούμε σε λείο οριζόντιο επίπεδο. Τραβώντας το νήμα για t=0 ασκούμε πάνω του οριζόντια δύναμη F, όπως στο σχήμα. Αν ως προς τον άξονα του κυλίνδρου Ι= 1/12 mR2.
α) Ο κύλινδρος θα κυλίεται χωρίς να ολισθαίνει.
β) Ο κύλινδρος θα εκτελέσει μόνο μεταφορική κίνηση ομαλά επιταχυνόμενη κίνηση.
γ) Ένα σημείο Α επαφής του κυλίνδρου με το επίπεδο έχει μηδενική ταχύτητα.
δ) Το σημείο Α έχει επιτάχυνση προς τα αριστερά.
Κύλιση τροχού και με ολίσθηση
Γύρω από έναν ομογενή κύλινδρο μάζας m=40kg και ακτίνας R=0,5m τυλίγουμε ένα αβαρές νήμα και κατόπιν τον τοποθετούμε σε οριζόντιο επίπεδο με το οποίο εμφανίζει συντελεστές τριβής μ=μs= 0,2. Τραβώντας το νήμα ασκούμε στον κύλινδρο μια σταθερή οριζόντια δύναμη F=120Ν.
i) Ποια η επιτάχυνση του κέντρου μάζας του κυλίνδρου.
ii) Βρείτε την τριβή που ασκείται στον κύλινδρο.
iii) Αν το μέτρο της δύναμης ήταν F=300Ν, ποια η επιτάχυνση του κέντρου μάζας του κυλίνδρου;
Δίνεται για τον κύλινδρο Ι= 1/2 mR2 και g=10m/s2.
Κύλιση τροχού χωρίς ολίσθηση
Ένας κύλινδρος μάζας 40kg και ακτίνας R=0,5m ηρεμεί σε οριζόντιο επίπεδο. Σε μια στιγμή t=0 ασκείται στον άξονά του μια σταθερή οριζόντια δύναμη F =60Ν, όπως στο σχήμα, με αποτέλεσμα ο κύλινδρος να αρχίσει να κυλίεται χωρίς να ολισθαίνει. Ζητούνται:
i) Η επιτάχυνση του κέντρου μάζας του κυλίνδρου.
ii) Η γωνιακή επιτάχυνση του κυλίνδρου.
iii) Το μέτρο της ασκούμενης τριβής.
iv) Τον ελάχιστο συντελεστή στατικής τριβής μεταξύ κυλίνδρου και επιπέδου, ώστε να μπορεί να κυλίεται ο κύλινδρος χωρίς να ολισθαίνει.
Δίνεται για τον κύλινδρο Ι= 1/2 mR2 και g=10m/s2.
Κίνηση συστήματος σωμάτων.
Το σώμα Σ του διπλανού σχήματος έχει μάζα m1 =2kg και ηρεμεί σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστή τριβής ολίσθησης μ=0,2. Δένουμε το σώμα στο άκρο νήματος, το οποίο αφού το περάσουμε από μια τροχαλία μάζας m2=2kg και ακτίνας R=0,2m, ασκούμε στο άλλο του άκρο μια σταθερή κατακόρυφη δύναμη F=10Ν. Το νήμα δεν γλιστράει στην τροχαλία. Ζητούνται:
i) Η επιτάχυνση του σώματος Σ.
ii) Η γωνιακή επιτάχυνση της τροχαλίας.
iii) Πόσες περιστροφές έχει πραγματοποιήσει η τροχαλία μέχρι τη στιγμή που αποκτά γωνιακή ταχύτητα ω=30rad/s.
Δίνεται g=10m/s2 ενώ για την τροχαλία Ι= 1/212 mR2.
Κατεύθυνση της Τριβής.
Μπορείτε να ερμηνεύσετε την κατεύθυνση της τριβής στα παρακάτω σχήματα;
Τροχός και Τριβή
Ένας τροχός εκτοξεύεται σε οριζόντιο επίπεδο με αρχική ταχύτητα υ0 και αρχική γωνιακή ταχύτητα ω0, όπως στα παρακάτω σχήματα.
Α) Να σχεδιάστε την τριβή που ασκείται στον τροχό σε κάθε περίπτωση.
Β) Σε ποια περίπτωση ασκείται μεγαλύτερη τριβή στον τροχό;
Γωνιακή Επιτάχυνση
Γύρω από μια τροχαλία τυλίγουμε ένα αβαρές νήμα, στο άκρο του οποίου ασκούμε κατακόρυφη δύναμη F. Η τροχαλία αποκτά γωνιακή επιτάχυνση αγων=5rad/s2. Αν στο άκρο του νήματος δέναμε ένα σώμα βάρους W= F, η γωνιακή επιτάχυνση της τροχαλίας θα ήταν:
α) ίση με 5rad/s2.
β) μικρότερη από 5rad/s2.
γ) μεγαλύτερη από 5rad/s2.
Γωνιακή επιτάχυνση ράβδου και επιτάχυνση σώματος δεμένο με νήμα με αυτήν.
Μια ομογενής οριζόντια δοκός ΑΓ μάζας m=10kg και μήκους 6m είναι αρθρωμένη στο άκρο της Α, ενώ στο άκρο της Γ είναι δεμένη με κατακόρυφο νήμα. Στο σημείο Δ της δοκού, όπου (ΑΔ)=2m, έχουμε κρεμάσει με νήμα μια σφαίρα Σ μάζας m1=6kg, όπως στο σχήμα. Σε μια στιγμή κόβεται το νήμα στο άκρο Γ. Για αμέσως μετά το κόψιμο του νήματος να βρεθούν:
i) Η γωνιακή επιτάχυνση της δοκού και
ii) Η επιτάχυνση της σφαίρας Σ.
iii) Αν (ΑΔ)=5m ποιες οι αντίστοιχες απαντήσεις σας;
Δίνεται η ροπή αδράνειας μιας δοκού ως προς κάθετο άξονα ο οποίος διέρχεται από το άκρον της Ι= 1/3 m·l2 και g=10m/s2.
Δύναμη από τον άξονα περιστροφής.
Συνισταμένη δύναμη και cm.
Ένα στερεό στρέφεται γύρω από έναν σταθερό άξονα. Τι συμβαίνει με την συνισταμένη των δυνάμεων που ασκούνται πάνω του;
α) Αν ο άξονας περνά από το κέντρο μάζας του στερεού, τότε το κέντρο μάζας παραμένει ακίνητο, οπότε ΣF=0.
β) Αν ο άξονας δεν περνά από το κέντρο μάζας, τότε θα εφαρμόσουμε τον θεμελιώδη της Μηχανικής για το κέντρο μάζας.
Πρέπει να τονισθεί ότι όταν το στερεό στρέφεται, το κέντρο μάζας του, εκτελεί κυκλική κίνηση με κέντρο το σημείο Α του άξονα.
Οπότε εφαρμόζουμε δυναμική για ένα υλικό σημείο που εκτελεί κυκλική κίνηση.
Έτσι αν η γωνιακή ταχύτητα του στερεού σώματος, παραμένει σταθερή το κέντρο μάζας θα εκτελεί ομαλή κυκλική κίνηση, οπότε η συνισταμένη θα είναι ίση με την κεντρομόλο:
ΣFR=mακ
ενώ αν υπάρχει γωνιακή επιτάχυνση του στερεού, το κέντρο μάζας θα έχει επιτρόχια επιτάχυνση και η συνισταμένη των δυνάμεων στη διεύθυνση της εφαπτομένης της κυκλικής τροχιάς θα είναι:
ΣFεφ= mαcm.
Παράδειγμα.
Μια ράβδος στρέφεται γύρω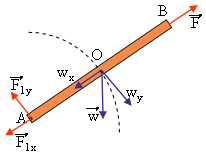 
από οριζόντιο άξονα που περνά από το ένα του άκρο Α και έστω ότι βρίσκεται στη θέση του διπλανού σχήματος, ενώ πάνω της ασκείται το βάρος της w, μια δύναμη F στο άκρο της Β και μια δύναμη από τον άξονα, η οποία αναλύεται στις συνιστώσες F1x και F1y.
Ας αναλύσουμε το βάρος σε μια διεύθυνση παράλληλη προς τη ράβδο wx και μια wy κάθετη στην ράβδο.
Εφαρμόζουμε τον θεμελιώδη νόμο της Μηχανικής, θεωρώντας ότι όλη η μάζα της ράβδου είναι συγκεντρωμένη στο κέντρο μάζας Ο και ότι όλες οι δυνάμεις ασκούνται στο Ο και παίρνουμε:
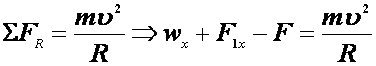(1)
ΣFκαθ =mαcm ή Wy ?F1y = mαcm (2)
Δηλαδή στην διεύθυνση της ακτίνας η συνισταμένη των δυνάμεων πάιζει το ρόλο της κεντρομόλου, ενώ σε κάθετη διεύθυνση η συνισταμένη είναι υπεύθυνη για την επιτάχυνση του κέντρου μάζας.
Ροπή αδράνειας και γωνιακή επιτάχυνση
Οι ομογενείς ράβδοι ΟΑ και ΑΒ με ίσες μάζες m=3kg και μήκη l1=4m και l2=6m αντίστοιχα, είναι συγκολλημένες όπως στο σχήμα. Το σύστημα μπορεί να στρέφεται γύρω από οριζόντιο άξονα, ο οποίος περνά από το άκρο Ο. Φέρνουμε το σύστημα σε τέτοια θέση, ώστε η ράβδος ΟΑ να είναι οριζόντια και το αφήνουμε να κινηθεί.Αν η ροπή αδράνειας μιας ράβδους ως προς κάθετο άξονα που περνά από το μέσον της δίνεται από τη σχέση Ι=1/12 ml2, να βρεθούν:
α) Η αρχική γωνιακή επιτάχυνση του συστήματος.
β) Η αρχική επιτάχυνση του μέσου Κ της ράβδου ΑΒ και να σχεδιαστεί στο σχήμα.
Κύλιση ή ολίσθηση του κυλίνδρου;
Ένας κύλινδρος βρίσκεται σε οριζόντιο επίπεδο και δέχεται την επίδραση σταθερής οριζόντιας δύναμης F η οποία ασκείται σε σημείο Α της περιφέρειάς του, όπως στο σχήμα.
i) Η ροπή της δύναμης:
α) έχει φορά προς τα δεξιά.
β) Είναι οριζόντια με μέτρο τ=FR.
γ) Είναι κάθετη στο επίπεδο της σελίδας με φορά προς τα μέσα στο σημείο Α.
δ) Είναι κάθετη στο επίπεδο της σελίδας με φορά προς τα μέσα στο σημείο Ο και μέτρο μικρότερο από το γινόμενο FR.
ii) Χαρακτηρίστε σαν σωστές ή λαθεμένες τις παρακάτω προτάσεις.
α) Ο κύλινδρος θα αποκτήσει γωνιακή επιτάχυνση προς τα δεξιά.
β) Η γωνιακή επιτάχυνση του κυλίνδρου έχει σταθερό μέτρο.
γ) Η γωνιακή ταχύτητα του κυλίνδρου θα δίνεται από τη σχέση ω=αγωνt.
δ) Η επιτάχυνση του σημείου Α έχει την κατεύθυνση της δύναμης F.
iii) Αν το επίπεδο είναι λείο:
α) Ο αρχικός ρυθμός μεταβολής της στροφορμής του κυλίνδρου είναι ίσος με μηδέν.
β) Η αρχική ισχύς της δύναμης είναι μηδενική.
γ) Ο κύλινδρος θα κυλίεται χωρίς να ολισθαίνει.
δ) Η αρχική επιτάχυνση του σημείου Γ είναι μηδενική.