- Το εμβαδό ενός τριγώνου είναι ίσο με το μισό του γινόμενου της βάσης του επί το αντίστοιχο ύψος. Αυτό εκφράζεται σύντομα με τον τύπο Ε (τριγώνου) = (β · υ) : 2
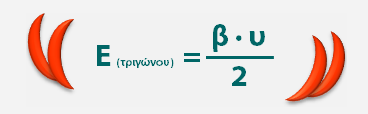
- Για να βρούμε το ύψος του τριγώνου, πρέπει να τραβήξουμε μια κάθετη γραμμή από μία από τις κορυφές του προς την απέναντι πλευρά. Αυτή η πλευρά του τότε λέγεται βάση του.

[slideboom id=768090&w=425&h=370]
Πατώντας Give hint βλέπεις ότι δυο τρίγωνα είναι ένα παραλληλόγραμμο,άρα το εμβαδόν τριγώνου θα είναι το μισό του
Δείτε πως διαμορφώνεται το ύψος του τριγώνου, ανάλογα με το είδος του
1. Εξασκήσου βρίσκοντας το Εμβαδό του τριγώνου..
2. Το ίδιο και εδώ. Βρες τα εμβαδά των τριγώνων
Πώς σχεδιάζουμε τα ύψη ενός τριγώνου:
α) Οξυγώνιο τρίγωνο
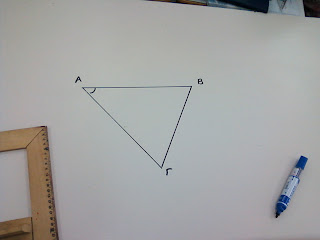
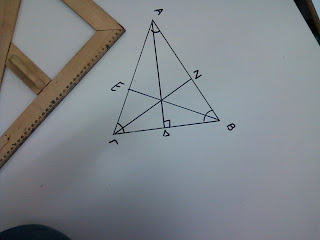
Σχεδιάζω ένα οξυγώνιο τρίγωνο ΑΒΓ. (κλικ στην εικόνα για μεγέθυνση)
Για να φέρω το ύψος από τη γωνία Α , εφαρμόζω τη μία κάθετη πλευρά του ορθογωνίου μου στην απέναντι πλευρά της γωνίας Α που είναι η ΒΓ.
Τη σέρνω μέχρι η άλλη κάθετη πλευρά να συναντήσει τη γωνία Α.
Και έτσι έχω το ύψος ΑΔ.
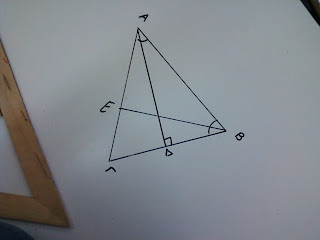
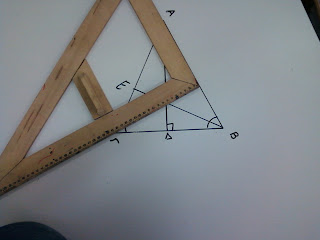
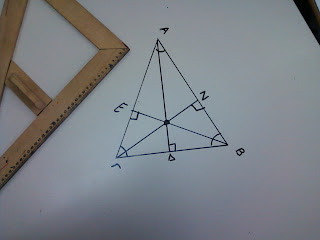
Με τον ίδιο τρόπο σχεδιάζω τα ύψη ΒΕ και ΓΖ.( Δείτε τις εικόνες.)
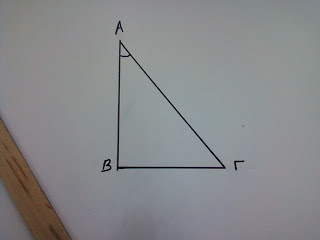
β) Ορθογώνιο τρίγωνο:
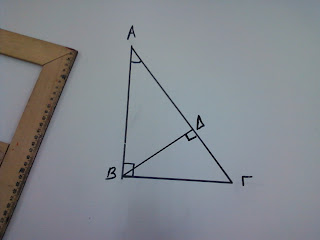
Έχουμε ένα ορθογώνιο τρίγωνο ΑΒΓ
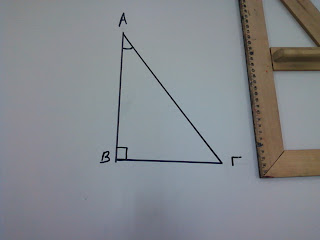
Παρατηρούμε ότι μόλις βάλουμε πάνω στην πλευρά ΒΓ,τη μία κάθετη πλευρά του γνώμονά μας και την άλλη να συναντήσει τη γωνία ,τότε το ύψος που σχηματίζεται είναι η πλευρά ΑΒ.
Άρα σε αυτήν την περίπτωση το ένα ύψος είναι η πλευρά ΑΒ.
Στη συνέχεια πάμε να βρούμε το ύψος που ξεκινά από τη γωνία Β
Φέρνω τη μιά κάθετη πλευρά του γνώμονά μου στην απέναντι πλευρά της γωνίας Β που είναι η ΑΓ.
Την άλλη κάθετη πλευρά την ταιριάζω στη γωνία Β.
Σχεδιάζω το ύψος ΒΔ.
Αφού λοιπόν βρήκαμε και το δεύτερο ύψος, πάμε να βρούμε και το τρίτο που ξεκινάει από τη γωνία Γ.
Βάζω τη μια κάθετη πλευρά του γνώμονά μου στην απέναντι πλευρά , την ΑΒ, και διαπιστώνω όπως στην πρώτη περίπτωση, ότι η πλευρά ΒΓ, είναι και το ύψος από τη γωνία Γ.
Άρα σε ένα ορθογώνιο τρίγωνο τα δύο από τα τρία ύψη , είναι οι δυο κάθετες πλευρές του.
Όλα τα ύψη του περνούν από το ίδιο σημείο ,που είναι το σημείο Β.
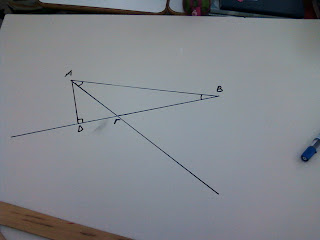
γ) Αμβλυγώνιο τρίγωνο
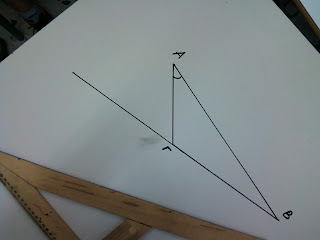
Έχω ένα αμβλυγώνιο τρίγωνο ΑΒΓ. Η αμβλεία γωνία είναι η Γ.
Ξεκινάω να φέρω το πρώτο ύψος από τη γωνία Α. Εφαρμόζω τη μία κάθετη πλευρά του γνώμονά μου στην απέναντι πλευρά ΒΓ. Βλέπω όμως ότι έτσι όπως είναι δεν με φτάνει για να συναντήσει η άλλη κάθετη πλευρά, τη γωνία Α.
Για αυτό το λόγο προεκτείνω τη ΒΓ ώστε να μπορώ να συναντήσω την Α γωνία.
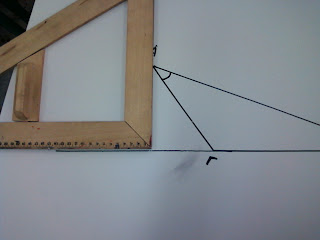
Έτσι αφού την προέκτεινα τοποθετώ ξανά τη μία κάθετη πλευρά του γνώμονα πάνω στην προέκταση της ΒΓ και τώρα πλέον μπορώ με την άλλη κάθετη πλευρά του να συναντήσω τη γωνία Α.
Ονομάζω το ύψος που σχηματίζεται ΑΔ κι έτσι έχω το πρώτο ύψος.
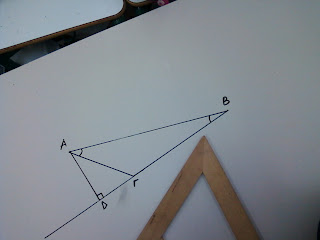
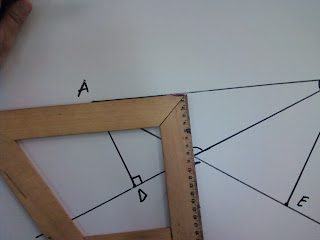
Στη συνέχεια πάω να φτιάξω το ύψος που ξεκινά από τη γωνία Β. Βάζω λοιπόν τη μία κάθετη πλευρά του γνώμονά μου στην απέναντι πλευρά της Β γωνίας που είναι η πλευρά ΑΓ. Βλέπω όμως όπως και στην πρώτη περίπτωση ότι δεν μου φτάνει για να συναντήσει η άλλη κάθετη πλευρά τη γωνία Β.
Για αυτό λοιπόν προεκτείνω την ΑΓ και γίνεται έτσι:
Πάνω στην προέκτασή της τοποθετώ τη μία κάθετη πλευρά του γνώμονά μου και στη γωνία Β την άλλη κάθετη πλευρά του. Σχεδιάζω το ύψος ΒΕ.
Έτσι έχω και το δεύτερο ύψος. Τώρα, μου λείπει το τρίτο ύψος που θα ξεκινήσει από τη γωνία Γ.
Τοποθετώ τη μία κάθετη πλευρά του γνώμονα στην απέναντι πλευρά της, την ΑΒ και την άλλη πάνω στην γωνία Γ.
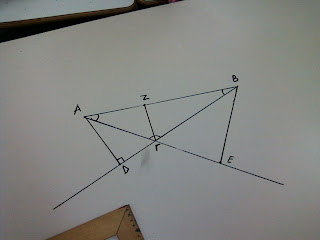
Έφτιαξα λοιπόν τα τρία ύψη του αμβλυγώνιου τριγώνου και παρατηρώ ότι τα δύο ύψη είναι εκτός (τα ΑΔ και ΒΕ) τριγώνου και το ένα εντός του (ΓΖ).
Για να δω αν συναντιούνται όλα στο ίδιο σημείο, πράγμα που δείχνει ότι είμαι σωστός στην κατασκευή μου , προεκτείνω και τα τρία ύψη.
Αν συναντηθούν στο ίδιο σημείο , τα κατάφερα μια χαρά. Αν όχι πρέπει να ξαναπροσπαθήσω.
Πηγή : http://ekaifigame.blogspot.gr/













Πρόσφατα σχόλια