Κεφ.22 – Εισαγωγή στα κλάσματα 1-2
Έχω μια σοκολάτα και τη χωρίζω σε δύο ίσα μέρη. Παίρνω το ένα από τα δύο ίσα μέρη. Το γράφω με
τον κλασματικό αριθμό:
Το διαβάζω “ένα δεύτερο”.
Όταν έχω λοιπόν μια μονάδα μπορώ να την χωρίσω (μοιράσω) σε ίσα μέρη.
Πχ: Ένα μπισκότο το χωρίζω σε 4 ίσα μέρη και παίρνω το ένα μέρος. Το γράφω με τον κλασματικό αριθμό:
και λέω ότι έχω πάρει το “ένα τέταρτο”
Τη σοκολάτα αυτή μπορώ να τη χωρίσω με πολλούς τρόπους εκτός από τον παραπάνω!
Για παράδειγμα μπορώ να τη χωρίσω έτσι και να λέω ότι πήρα το “ένα έκτο” ή το “ένα τρίτο”:
Αριθμητής και Παρονομαστής
Σε ένα κλάσμα το πάνω μέρος το ονομάζουμε αριθμητή και το κάτω παρονομαστή.
Άξονας συμμετρίας
Ο άξονας συμμετρίας χωρίζει το σχήμα σε δύο ίσα μέρη.
Πχ: Ένα ορθογώνιο παραλληλόγραμμο μπορεί να χωριστεί σε δύο ίσα μέρη με 2 διαφορετικούς τρόπους.
ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ
Κεφ.23 – Οι κλασματικές μονάδες
Χωρίζω τον κύκλο σε δύο μέρη, μετά τον χωρίζω σε τέσσερα ίσα μέρη και στη συνέχεια τον χωρίζω σε οκτώ ίσα μέρη.
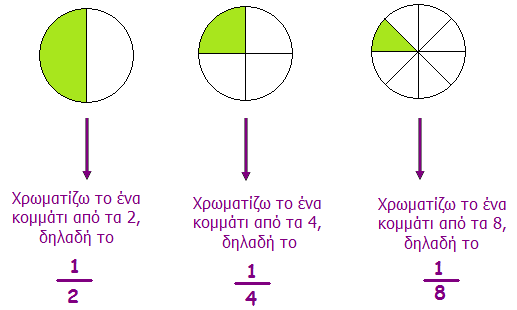
Τα 
είναι κλασματικές μονάδες, γιατί κάθε φορά παίρνω ένα κομμάτι από αυτά που χώρισα (μοίρασα).
Παρατήρηση:
Όσο μεγαλύτερος είναι ο παρονομαστής, τόσο μικρότερο είναι το κομμάτι που θα πάρουμε.
Για παράδειγμα αν έχω δύο ίδιες σοκολάτες και χωρίσω τη μία σε δύο κομμάτια και την άλλη σε 3 κομμάτια και φάω το ένα κομμάτι από κάθε σοκολάτα θα φάω περισσότερο από την πρώτη σοκολάτα.
Κλασματική μονάδα έχω όταν παίρνω το ένα από τα ίσα μέρη στα οποία έχω χωρίσει (μοιράσει) την ακέραια μονάδα. Αριθμητής σε μια κλασματική μονάδα είναι το 1.
ΚΑΡΤΕΛΕΣ
ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ
Κεφ.24 – Οι κλασματικές μονάδες και οι απλοί κλασματικοί αριθμοί
Κλασματικοί αριθμοί
Παραδείγματα κλασματικών αριθμών:
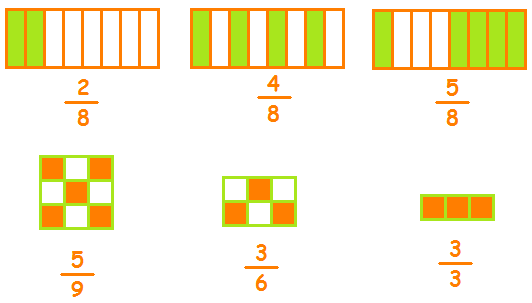
Στο τελευταίο σχήμα παρατηρούμε ότι οι κλασματικοί αριθμοί που έχουν ίδιο αριθμητή και παρονομαστή είναι ίσοι με την ακεραία μονάδα.
Πχ:
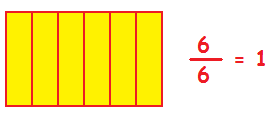
Στο διπλανό σχήμα έχουμε χρωματίσει και τα 6 κομμάτια του ορθογωνίου. Το έχουμε δηλαδή χρωματίσει όλο. Οπότε μπορούμε να πούμε ότι ισούται με τη μονάδα (1).
Προσοχή: Αν μου δώσουν ένα σχήμα σαν αυτό:
και μου πουν να χρωματίσω το 
ενώ το σχήμα είναι χωρισμένο σε 4 κομμάτια θα πρέπει να σκεφτώ έναν τρόπο να το ξαναχωρίσω σε 2 κομμάτια. Δηλαδή:
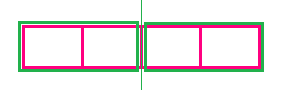
Έτσι θα το έχω χωρίσει σε δύο κομμάτια και θα μπορώ να χρωματίσω το . Δηλαδή:
Δραστηριότητα από το skoool.gr. Κάνε κλικ εδώ.
ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ
Κεφ.25 – Ισοδύναμα Κλάσματα
Οι κλασματικοί αριθμοί που έχουν διαφορετικό αριθμητή και διαφορετικό παρονομαστή ο ένας από τον άλλο, αλλά έχουν ίση αξία, ονομάζονται ισοδύναμα κλάσματα.
Παράδειγμα:
Και στα τρία παραπάνω όμοια σχήματα έχουμε χρωματίσει το ίδιο μέρος παρόλο που δεν έχουν τον ίδιο κλασματικό αριθμό. Έτσι λέμε ότι τα παραπάνω κλάσματα είναι ισοδύναμα και τα συμβολίζουμε έτσι:
Παράδειγμα με το ευρώ
 |
Τι μέρος του ενός ευρώ είναι ένα νόμισμα των 50 λεπτών;
Τι μέρος του ενός ευρώ είναι 5 νομίσματα των 10 λεπτών;
Τι παρατηρούμε;
Τα παραπάνω κλάσματα είναι ισοδύναμα. |
ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ
https://blogs.sch.gr/andromachig/files/2023/07/Κεφ.25_-_Ισοδύναμα_Κλάσματα.pdf
ΕΠΑΝΑΛΗΨΗ
- Θυμάμαι τι είναι το κλάσμα και τα μέρη του (βλ. κεφ.22).
- Θυμάμαι ποιες είναι οι κλασματικές μονάδες (βλ. κεφ.23).
- Θυμάμαι τι είναι ο άξονας συμμετρίας (βλ. κεφ.23).
- Θυμάμαι ποιοι είναι οι απλοί κλασματικοί αριμοί (βλ. κεφ.24).
- Θυμάμαι τι είναι τα ισοδύναμα κλάσματα (βλ. κεφ. 25)
ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ
