Το ατομικό παιχνίδι « Ο Πύργος του Ανόι » που κυκλοφορεί στο εμπόριο, αποτελείται από τρεις κατακόρυφους άξονες Α, Β, και Γ και μερικούς άνισου μεγέθους δίσκους.
Το πρόβλημα είναι το εξής:
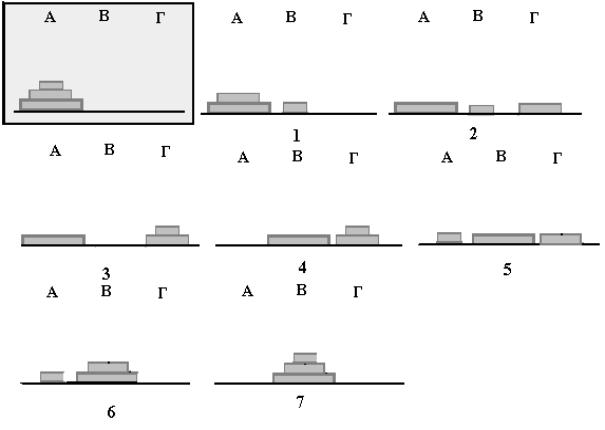
Πρέπει να μεταφερθεί ο Πύργος από τη θέση Α στη θέση Β ή στη θέση Γ, χρησιμοποιώντας την τρίτη θέση σαν βοηθητική, και μετακινώντας κάθε φορά μόνο ένα δίσκο, αλλά με τον περιορισμό πως δεν μπορεί να τοποθετηθεί ένας μεγαλύτερος δίσκος πάνω σ’ ένα μικρότερο. Το παιχνίδι που κυκλοφορεί στην αγορά έχει 7 δίσκους.
Ιστορία παιχνιδιού:
Το παιχνίδι ονομάσθηκε « Πύργος του Ανόι » από το σχήμα του πύργου που θυμίζει την αρχιτεκτονική των ναών στις χώρες της Άπω ανατολής.
Το παιχνίδι πρωτοεμφανίστηκε από τον Γάλλο μαθηματικό Έντουαρτ Λούκας γύρω στα 1883 με προέλευση μάλλον από τις Ινδίες.
Υπάρχει για το παιχνίδι ο παρακάτω θρύλος με τίτλο « Πύργος του Βράχμα »
«Όταν ο Βράχμα δημιούργησε τον κόσμο, έστησε σένα ναό στην πόλη Μπενάρες, 64 δακτυλίδια άνισου μεγέθους όλα περασμένα σένα μπαστούνι έτσι ώστε αν κρατήσουμε το μπαστούνι κατακόρυφα να σχηματίζουν τον γνωστό μας πύργο
Oι ιερείς του ναού έπρεπε να δουλεύουν μέρα νύχτα, χωρίς σταμάτημα, για να μεταφέρουν τα δακτυλίδια σένα άλλο μπαστούνι, χρησιμοποιώντας ένα τρίτο σαν βοηθητικό, έτσι ώστε να μην τοποθετήσουν μεγαλύτερο δακτυλίδι πάνω από μικρότερο και μετακινώντας ένα μόνο δακτυλίδι σε κάθε κίνηση.
Ο θρύλος λέει πως πριν προλάβουν οι ιερείς να μεταφέρουν όλα τα δακτυλίδια στο άλλο μπαστούνι, ο ναός θα καταρρεύσει μέσα στην σκόνη και ο κόσμος θα χαθεί μέσα σε τρομακτικό κρότο βροντής».
Το μαθηματικό πρόβλημα
Το πρόβλημα να βρεθεί ο αριθμός των κινήσεων που απαιτούνται για την μεταφορά και των 64 δίσκων φυσικά και υπάρχει, αποδεικνύεται ότι για την μεταφορά ν δίσκων απαιτούνται 2ν -1 κινήσεις, άρα για το συγκεκριμένο παράδειγμα αν για κάθε κίνηση απαιτείται 1 δευτερόλεπτο απαιτούνται 2 64-1 κινήσεις, ισοδύναμο χρονικά με 500.000.000.000 χρόνια.
Ας δούμε λίγο πως αντιμετωπίζεται το πρόβλημα. Ας υποθέσουμε ότι έχουμε 4 δίσκους για να τους μεταφέρουμε από τον στύλο Α στο στύλο Β. Δίνουμε αύξοντα αριθμό από το 1 μέχρι το 4 στους δίσκους από την κορυφή και κάτω. Οι κανόνες είναι απλοί:
1.Πάντα μεταφέρουμε του δίσκους με περιττή αρίθμηση στην πρώτη τους κίνηση από τον στύλο Α στον Γ ,ενώ τους δίσκους με άρτια αρίθμηση τους μεταφέρουμε στην πρώτη τους κίνηση από τον στύλο Α στον στύλο Β.
2.Μεταφέρουμε τον δίσκο 1 κάθε δεύτερη κίνηση , τον δίσκο 2 κάθε τετάρτη κίνηση τον δίσκο 3 κάθε όγδοη κίνηση κ.ο.κ.
Οι πύργοι του Ανόι είναι δημοφιλής άσκηση σε εισαγωγικά μαθήματα προγραμματισμού καθώς απαιτείται συγκεκριμένος αλγόριθμος για την επίλυση του προβλήματος. Το παιχνίδι-με πολύ λιγότερους δίσκους-βγήκε στο εμπόριο σε διάφορες εκδοχές του πάμπολλες φορές τα τελευταία 120 χρόνια. Επίσης οι Πύργοι του Ανόι χρησιμοποιούνται από τους ψυχολόγους για τη μέτρηση της λειτουργίας ή δυσλειτουργίας των προμετωπιαίων λοβών.



Ήταν ένα πολύ ενδιαφέρον θέμα.