Η λίστα των 10 ομορφότερων πειραμάτων είναι:
Η λίστα των 10 ομορφότερων πειραμάτων είναι:
2. Το πείραμα του Γαλιλαίου για την ελεύθερη πτώση (1600)

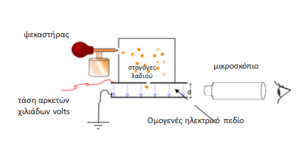
Στην κορυφή και στη βάση του θαλάμου υπήρχαν μεταλλικές πλάκες συνδεδεμένες με μπαταρία δημιουργώντας έναν θετικό και έναν αρνητικό πόλο. Εφόσον κάθε σταγονίδιο λάμβανε ένα ελάχιστο φορτίο στατικού ηλεκτρισμού καθώς ταξίδευε στον αέρα, η ταχύτητα της κίνησής του μπορούσε να ελεγχθεί με αλλαγές της τάσης στις δύο πλάκες. Όταν ο χώρος μεταξύ των δύο πλακών ιονίζεται με ακτινοβολία, τα ηλεκτρόνια του αέρα κολλάνε στα σταγονίδια του λαδιού προσδίδοντάς τους αρνητικό φορτίου. Ο Millikan παρατήρησε πολλά σταγονίδια μεταβάλλοντας την τάση και ελέγχοντας το αποτέλεσμα. Μετά από πολλές επαναλήψεις συμπέρανε ότι το φορτίο μπορεί να λάβει μόνο κάποιες συγκεκριμένες τιμές. Οι μικρότερες από τις τιμές αυτές αντιστοιχούν στο φορτίο του ηλεκτρονίου.
 Σύμφωνα με τον Αριστοτέλη και την κοινή λογική της εποχής, το λευκό φως θεωρείτο ότι είναι η πιο καθαρή μορφή και ότι το έγχρωμο φως πρέπει κάπως να έχει παραμορφωθεί. Για να ελέγξει αυτή την υπόθεση ο Νεύτωνας πέρασε μια δέσμη ηλιακού φωτός μέσα από ένα γυάλινο πρίσμα και έδειξε ότι αναλυόταν σε ένα φάσμα το οποίο στη συνέχεια έπεφτε πάνω σε ένα τοίχο. Οι άνθρωποι βέβαια ήδη γνώριζαν για το ουράνιο τόξο αλλά πίστευαν ότι οφειλόταν σε κάποιες αποκλίσεις του φωτός.
Σύμφωνα με τον Αριστοτέλη και την κοινή λογική της εποχής, το λευκό φως θεωρείτο ότι είναι η πιο καθαρή μορφή και ότι το έγχρωμο φως πρέπει κάπως να έχει παραμορφωθεί. Για να ελέγξει αυτή την υπόθεση ο Νεύτωνας πέρασε μια δέσμη ηλιακού φωτός μέσα από ένα γυάλινο πρίσμα και έδειξε ότι αναλυόταν σε ένα φάσμα το οποίο στη συνέχεια έπεφτε πάνω σε ένα τοίχο. Οι άνθρωποι βέβαια ήδη γνώριζαν για το ουράνιο τόξο αλλά πίστευαν ότι οφειλόταν σε κάποιες αποκλίσεις του φωτός.Στη πραγματικότητα ο Νεύτωνας έδειξε ότι τα χρώματα στα οποία αναλυόταν το λευκό φως ήταν τα βασικά χρώματα: το ερυθρό, το πορτοκαλί, το κίτρινο, το πράσινο, το μπλε, το ιώδες και οι διαβαθμίσεις μεταξύ τους. πηγή
5. Το πείραμα του Young για την συμβολή του φωτός (1801)
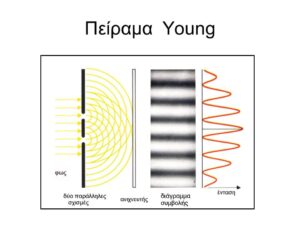
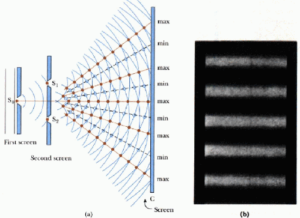
Η συμβολή παρατηρήθηκε με το πείραμα Δύο Σχισμών του φυσικού Thomas Young το 1801 το οποίο επιβεβαίωσε την κυματική φύση του φωτός.Σύμφωνα με το Πείραμα Young το φως μίας μονοχρωματικής πηγής προσπίπτει σε ένα διάφραγμα στο οποίο είναι χαραγμένες δύο παράλληλες πολύ λεπτές σχισμές.
Το αποτέλεσμα είναι να σχηματίζεται στο πέτασμα (σε μία οθόνη) πίσω από τις σχισμές μία εικόνα από εναλλασσόμενες φωτεινές και σκοτεινές ζώνες. Το σχέδιο που δημιουργείται ονομάζεται εικόνα συμβολής και αποτελείται από διαδοχικούς φωτεινούς και σκοτεινούς κροσσούς, τους κροσσούς συμβολής. Το πείραμα αυτό επαναλήφθηκε με την πάροδο των ετών. Αυτά τα πειράματα που λέγονται πειράματα των δύο σχισμών καθιέρωσαν την κυματική φύση του φωτός.

Ο Βρετανός επιστήμονας Henry Cavendish διεξήγαγε, για πρώτη φορά το 1797-1798, το πρώτο πείραμα μέτρησης της δύναμης της βαρύτητας ανάμεσα σε δύο μάζες στο εργαστήριο και το πρώτο που έδωσε ακριβείς τιμές για την παγκόσμια σταθερά της βαρύτητας.
Πήρε μια ξύλινη ράβδο μήκους περίπου 1,5 μέτρων και κόλλησε μικρές μεταλλικές σφαίρες σε κάθε άκρο της όπως σ’ έναν αλτήρα. Μετά την κρέμασε από ένα σύρμα. Δύο μολυβένιες σφαίρες 350 λιβρών η κάθε μια τοποθετήθηκαν κοντά στις σφαίρες της ράβδου και ασκούσαν σ’ αυτές υπολογίσιμες δυνάμεις ώστε να προκαλέσουν την περιστροφή της ράβδου και την συστροφή του σύρματος που την κρατούσε. Με μετρήσεις ακριβείας μπορούσε να μετρήσει την μικρή περιστροφή της ράβδου. 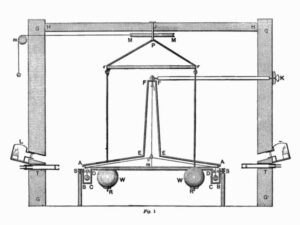 Για να αποφύγει την επίδραση των ρευμάτων του αέρα, η συσκευή κλείστηκε σ’ ένα δωμάτιο και οι παρατηρήσεις γίνονταν απ’ έξω με τηλεσκόπια.
Για να αποφύγει την επίδραση των ρευμάτων του αέρα, η συσκευή κλείστηκε σ’ ένα δωμάτιο και οι παρατηρήσεις γίνονταν απ’ έξω με τηλεσκόπια.
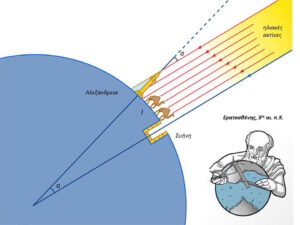
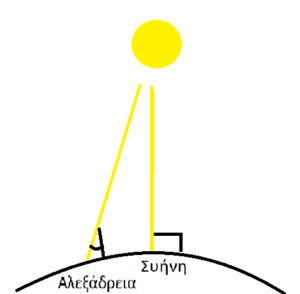 ηλιοστασίου, οι ακτίνες του Ήλιου στη Συήνη (Ασουάν) πέφτουν κάθετα. Βασισμένος σε αυτό, τοποθέτησε ένα κοντάρι κάθετα στο έδαφος στην Αλεξάνδρεια και μέτρησε τη γωνία μεταξύ του κονταριού και των ακτίνων του ήλιου. Επειδή η απόσταση Γης-Ήλιου είναι μεγάλη, οι ακτίνες πέφτουν σχεδόν παράλληλα. Άρα αυτή η γωνία είναι σχεδόν ίση με τη γωνία του κυκλικού τόξου Αλεξάνδρειας – Συήνης ως εντός εναλλάξ.
ηλιοστασίου, οι ακτίνες του Ήλιου στη Συήνη (Ασουάν) πέφτουν κάθετα. Βασισμένος σε αυτό, τοποθέτησε ένα κοντάρι κάθετα στο έδαφος στην Αλεξάνδρεια και μέτρησε τη γωνία μεταξύ του κονταριού και των ακτίνων του ήλιου. Επειδή η απόσταση Γης-Ήλιου είναι μεγάλη, οι ακτίνες πέφτουν σχεδόν παράλληλα. Άρα αυτή η γωνία είναι σχεδόν ίση με τη γωνία του κυκλικού τόξου Αλεξάνδρειας – Συήνης ως εντός εναλλάξ.
Άρα:μετρημένη γωνία/360 μοίρες =τόξο / περιφέρεια της γης άρα:
περιφέρεια της γης= 360 μοίρες x τοξο/ μετρημένη γωνία.
Η γωνία που μέτρησε είναι 7,2μοιρες. Μετά από αυτή τη διαδικασία βρήκε ότι η 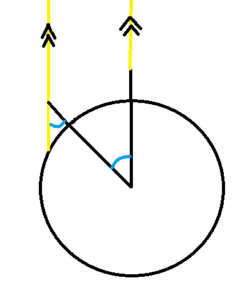 περιφέρεια της Γης κυμαίνεται από39.000 έως 46.000 Km. Η τιμή που έχουμε βρει σήμερα ως την περιφέρεια της Γης είναι 40.008 Km. Επομένως η σωστή τιμή βρίσκεται μέσα στους υπολογισμούς του Ερατοσθένη.
περιφέρεια της Γης κυμαίνεται από39.000 έως 46.000 Km. Η τιμή που έχουμε βρει σήμερα ως την περιφέρεια της Γης είναι 40.008 Km. Επομένως η σωστή τιμή βρίσκεται μέσα στους υπολογισμούς του Ερατοσθένη.
Ο Γαλιλαίος συνέχισε να τελειοποιεί τις ιδέες του για την κίνηση των σωμάτων. Πήρε μια σανίδα με μήκος περίπου 4μέτρα και πλάτος περί τα 20cm και δημιούργησε στο μέσον της ένα αυλάκι όσο πιο ίσιο και λείο μπορούσε. Την τοποθέτησε ως κεκλιμένο επίπεδο και άφησε να κυλήσουν μέσα στο αυλάκι χάλκινες σφαίρες, χρονομετρώντας την κάθοδό τους με ένα ρολόι που δούλευε με νερό. Επρόκειτο για ένα μεγάλο δοχείο που άδειαζε από ένα μικρό σωληνάκι μέσα σε μικρότερα ογκομετρικά δοχεία. Μετά από κάθε πείραμα ογκομετρούσε το νερό που είχε χυθεί, και αναλογικά συμπέραινε πόσος χρόνος είχε περάσει. Συνέκρινε στη συνέχεια τους χρόνους που αντιστοιχούσαν σε διαφορετικές αποστάσεις κίνησης των σφαιρών.
Ο Αριστοτέλης θα προέβλεπε ότι η ταχύτητα των σφαιρών ήταν σταθερή. Δηλαδή διπλασιάζοντας την απόσταση θα περνούσε και διπλάσιος χρόνος. Ο Γαλιλαίος όμως μπόρεσε να δείξει ότι η απόσταση ήταν στην πραγματικότητα ανάλογη με το τετράγωνο του χρόνου. Ο λόγος βέβαια είναι ότι η σφαίρα επιταχύνεται σταθερά από την βαρύτητα και η ταχύτητά της αυξάνει ανάλογα με τον χρόνο.
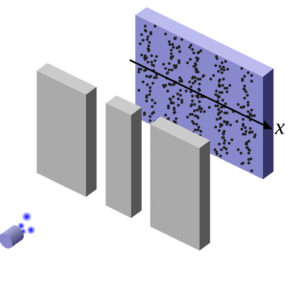
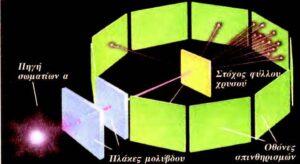
Παρατήρησαν ότι στη συντριπτική τους πλειοψηφία τα σωματίδια ακολουθούσαν σχεδόν ευθείες τροχιές, αρκετά παρέκλιναν από την αρχική τους διεύθυνση, υπήρχαν όμως κάποια που εκτρέπονταν κατά πολύ μεγάλες γωνίες ή επέστρεφαν πίσω. Αυτές οι μεγάλες αποκλίσεις δεν μπορούσαν να εξηγηθούν από το ατομικό μοντέλο του Thomson. Σύμφωνα με το μοντέλο του Thomson (το μοντέλο του “σταφιδόψωμου”) τα άτομα αποτελούνταν από συμπαγείς μάζες με θετικό ηλεκτρικό φορτίο, ενώ στο εσωτερικό τους βρίσκονταν τα ηλεκτρόνια ομοιόμορφα κατανεμημένα. Αν ίσχυε το μοντέλο του Thomson, τα σωματίδια θα απόκλιναν ελάχιστα της πορείας τους. Έτσι στο πρότυπο του Rutherford το άτομο αποτελείται από μία πολύ μικρή περιοχή, στην οποία είναι συγκεντρωμένο όλο το θετικό φορτίο και σχεδόν όλη η μάζα του ατόμου. Η περιοχή αυτή ονομάζεται πυρήνας. Ο πυρήνας περιβάλλεται από ηλεκτρόνια. Τα ηλεκτρόνια πρέπει να κινούνται γύρω από τον πυρήνα σε κυκλικές τροχιές, όπως οι πλανήτες γύρω από τον Ήλιο, γιατί αν ήταν ακίνητα θα έπεφταν πάνω στον πυρήνα εξαιτίας της ηλεκτρικής έλξης που δέχονται από αυτόν.
Το πρότυπο του Rutherford ονομάζεται και πλανητικό μοντέλο του ατόμου, γιατί αποτελεί μικρογραφία του ηλιακού πλανητικού συστήματος. Αποτελεί ένα μεγάλο βήμα, που πλησιάζει στην εικόνα του ατόμου όπως τη γνωρίζουμε σήμερα.
Ο Φουκώ προσκάλεσε τους επιφανείς Παριζιάνους επιστήμονες, για να είναι μάρτυρες στην επίδειξη του πειράματός του, γράφοντας προσκλήσεις: “Προσκαλείστε να δείτε τη γη που περιστρέφεται”. Χρησιμοποιώντας ένα ατσάλινο νήμα μήκους 67 μέτρων, άφησε μία σιδερένια σφαίρα βάρους 28 κιλών να αιωρηθεί από τον θόλο του Πάνθεου, κινούμενη μπροστά και πίσω. Για να καταγράψει την κίνησή της, στερέωσε μια μικρή ράβδο στη σφαίρα, η οποία αποτύπωνε την τροχιά του εκκρεμούς σε μία επιφάνεια στρωμένη με άμμο, στο έδαφος κάτω από τη σφαίρα, καταγράφοντας την τροχιά της μπάλας σε σχέση με το πάτωμα.