Οι Φυσικές Επιστήμες στο σχολείο… και όχι μόνο

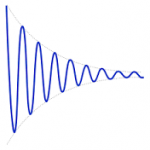
Οι μαθητές χωρίζονται σε ομάδες. Αφού εφαρμόσουν το Θεμελιώδη Νόμο της Μηχανικής για την περίπτωση της δύναμης επαναφοράς σε συνδυασμό με δύναμη υγρής τριβής της μορφής -bυ, το επιλύουν με τη βοήθεια του περιβάλλοντος προσομοιώσεων Modellus X, δημιουργώντας τη δική τους προσομοίωση Φθίνουσας Ταλάντωσης. Mε τη βοήθεια της παραπάνω προσομοίωσης σχεδιάζουν:

1. Τα διαγράμματα απομάκρυνσης- χρόνου, ταχύτητας- χρόνου και επιτάχυνσης- χρόνου για ίδιες τιμές της αρχικής ταχύτητας και θέσης, σταθεράς επαναφοράς και μάζας αλλά για διάφορεςς τιμές της σταθεράς απόσβεσης.
2. Τα συγκριτικά διαγράμματα απομάκρυνσης- χρόνου, ταχύτητας- χρόνου και επιτάχυνσης- χρόνου για κοινές τιμές των παραμέτρων της κίνησης αλλά διάφορες τιμές της αρχικής ταχύτητας και θέσης (όταν έχουμε φθίνουσα ταλάντωση).
3. Το κοινό διάγραμμα κινητικής ενέργειας- χρόνου, δυναμικής ενέργειας- χρόνου και ολικής ενέργειας- χρόνου για διάφορες τιμές της αρχικής ταχύτητας και θέσης όταν το σώμα εκτελεί φθίνουσα ταλάντωση (κοινές τιμές των υπόλοιπων παραμέτρων).
4. Το κοινό διάγραμμα κινητικής ενέργειας- απομάκρυνσης, δυναμικής ενέργειας- απομάκρυνσης και ολικής ενέργειας- απομάκρυνσης για διάφορες τιμές της αρχικής ταχύτητας και θέσης (κοινές τιμές μάζας και σταθεράς επαναφοράς).

Μελετάμε τις γραφικές παραστάσεις που προέκυψαν:

1. Πώς η αλλαγή της σταθεράς απόσβεσης επηρεάζει την κίνηση του σώματος; Για ποιες τιμές της σταθεράς απόσβεσης παρατηρείται φθίνουσα ταλάντωση; Τι συμβαίνει στις υπόλοιπες περιπτώσεις; Επιδρά η μάζα του σώματος στο είδος της κίνησής του και πώς;
2. Τι συμπεραίνουμε για τη διαφορά φάσης μεταξύ απομάκρυνσης και επιτάχυνσης, μεταξύ ταχύτητας και επιτάχυνσης και μεταξύ απομάκρυνσης και ταχύτητας;
3. Πώς η τυχόν αλλαγή των αρχικών συνθηκών (αρχική απομάκρυνση και ταχύτητα) επηρεάζει τη μορφή των παραπάνω διαγραμμάτων;
4. Ποια μεγέθη της Απλής Αρμονικής Ταλάντωσης επηρεάζονται από τη μεταβολή της μάζας του σώματος ή της σταθεράς επαναφοράς;
5. Τι συμπεραίνουμε για την ολική ενέργεια σε συνάρτηση με του σώματος σε συνάρτηση με το χρόνο; Είναι της μορφής E = Eo.exp(-γt);

Η υπολογιστική προσομοίωση σε Modellus X:

Τα αρχεία των μαθητών

Το σχέδιο του μαθήματος σε Learning Designer (στα Αγγλικά, για συναδέλφους):

https://v.gd/ppYV3B