Στις 3 Δεκεμβρίου 2025 με αφορμή την Παγκόσμια Ημέρα Αναπηρίας, μαθητές και μαθήτριες του 1ου Γυμνασίου Καρπενησίου συμμετείχαν σε ποικίλες δράσεις, που στόχο είχαν την καλλιέργεια ενσυναίσθησης, σεβασμού και αποδοχής της διαφορετικότητας.

Στο πλαίσιο της Ημέρας, μαθητές/τριες συμμετείχαν, υπό την καθοδήγηση της Διευθύντριας του Γυμνασίου/ καθηγήτριας Φυσικής Αγωγής, κας Βασιλικής Σιούτα, σε αθλήματα παραλλαγής (adapted sports), όπως πετοσφαίριση καθιστών ένα από τα σημαντικότερα ομαδικά αθλήματα για αθλητές με αναπηρία. Σκοπός των αθλητικών δράσεων ήταν να γίνουν κατανοητές    στους μαθητές/τριες με βιωματικό τρόπο οι δυσκολίες που αντιμετωπίζουν τα άτομα με αναπηρία και να αναπτύξουν ενσυναίσθηση, σεβασμό και αποδοχή της διαφορετικότητας.

 Επιπροσθέτως, στο πλαίσιο της Ημέρας, προβλήθηκαν, από την Φιλόλογο Ειδικής Αγωγής Ουρ. Μπαλογιάννη, βίντεο και σειρά διαφανειών -ειδικά επιλεγμένες- ώστε να αναδειχθούν οι καθημερινές προκλήσεις, αλλά και οι δυνατότητες των ατόμων με αναπηρία. Μέσα από εικόνες, ιστορίες και παραδείγματα, τα παιδιά ήρθαν σε επαφή με έννοιες, όπως η ισότητα ευκαιριών, η προσβασιμότητα και η συμπερίληψη. Οι προβολές συνοδεύτηκαν από συζήτηση, στην οποία οι μαθητές/τριες εξέφρασαν σκέψεις, προβληματισμούς και ενδιαφέροντα ερωτήματα. Οι δράσεις ολοκληρώθηκαν με εικαστικές δημιουργίες των μαθητών/τριών, οι οποίες ενίσχυσαν τη συνεργασία και βοήθησαν τα παιδιά να συνειδητοποιήσουν πως κάθε άνθρωπος, ανεξάρτητα από τις δυσκολίες που αντιμετωπίζει, έχει μοναδικά ταλέντα και δυνατότητες.

 Οι δράσεις που υλοποιήθηκαν με αφορμή την Ημέρα Αναπηρίας βοήθησαν τους μαθητές/τριες να κατανοήσουν βαθύτερα τη σημασία της αποδοχής, της ενσυναίσθησης και της ισότητας, ενισχύοντας μια σχολική κουλτούρα, στην οποία κάθε άνθρωπος έχει θέση, αξία και φωνή. Όλοι μαζί καταλήξαμε ότι: «διαβάΖΟΥΜΕ όλοι μαζί!!!».

 Για την υλοποίηση της δράσης σημαντική ήταν η συμβολή των εκπαιδευτικών του σχολείου μας κ.κ. Μαργ. Τσακανίκα, Αγγελ. Ρουμπιέ και Σπ. Σαρρή. Τους ευχαριστούμε θερμά.

ΩΡΕΣ ΕΝΗΜΕΡΩΣΗΣ ΓΟΝΕΩΝ 2025-26

Υπεύθυνη δήλωση για την παρακολούθηση μαθημάτων στο πλαίσιο του προγράμματος της Ενισχυτικής Διδασκαλίας

Υπόδειγμα_1_ΕΝΔ ΓΥΜΝ_αίτησης_δήλωσης μαθ_2025_26

Αγαπητοί Γονείς,

Σας ενημερώνουμε ότι το Κέντρο Πρόληψης των Εξαρτήσεων και Προαγωγής της Ψυχοκοινωνικής Υγείας Π.Ε. Ευρυτανίας «Αλκυόνη» διοργανώνει ομιλία με θέμα: «Δεξιότητες του Σύγχρονου Γονέα».

Η εκδήλωση θα πραγματοποιηθεί την Παρασκευή 14 Νοεμβρίου 2025, στις 18:00, στο Συνεδριακό Κέντρο Καρπενησίου, με ομιλητή τον διακεκριμένο ψυχολόγο κ. Ιωάννη Γλωσσόπουλο και απευθύνεται σε όλους τους γονείς του νομού Ευρυτανίας

Ο κ. Ιωάννης Γλωσσόπουλος, διαθέτει πολυετή εμπειρία στον τομέα της παιδικής και εφηβικής ψυχολογίας. Μέσα από την επιστημονική του γνώση και τη βιωματική του προσέγγιση, μπορεί να συμβάλει ουσιαστικά στην ενδυνάμωση της σχέσης ανάμεσα σε γονείς και παιδιά.

Η ομιλία, θα εστιάσει στην παροχή πρακτικών εργαλείων, στρατηγικών και τεχνικών που μπορούν να βοηθήσουν τους γονείς να υιοθετήσουν πιο θετικές και αποτελεσματικές προσεγγίσεις στην ανατροφή των παιδιών τους.

Μέσα από ένα βιωματικό πλαίσιο, οι συμμετέχοντες θα έχουν την ευκαιρία να εκφράσουν τους προβληματισμούς τους και να αναπτύξουν νέες δεξιότητες διαχείρισης των καθημερινών προκλήσεων της οικογενειακής ζωής.

Η είσοδος είναι ελεύθερη για όλους.

Λήψη αρχείου

Ο Αγιασμός των σχολείων (1ο Γυμνάσιο, Γενικό Λύκειο και ΕΠΑΛ Καρπενησίου) θα πραγματοποιηθεί την Πέμπτη 11 Σεπτεμβρίου 2025 και ώρα 11:00 π.μ. στο Αμφιθέατρο της Βασικής Βιβλιοθήκης.

Με αφορμή τη Διεθνή Ημέρα Μουσείων , στις 18 Μαΐου, οι μαθητές της Α΄Γυμνασίου Τσαρούχης Χ. και Τσουκαλάς Π. γράφουν για τα μουσεία της Θεσσαλονίκης:

Τα μουσεία είναι υπέροχα να τα επισκέπτεσαι διότι είναι ενδιαφέρον για τον κόσμο να μάθει για τον πολιτισμό και για αρχαία πράγματα .

Υπάρχουν πολλά είδη μουσείων στην Θεσσαλονίκη όπως το Αρχαιολογικό μουσείο που μιλάει για την ιστορία της πόλης, το Εβραϊκό μουσείο και  το Παιδικό Μουσείο Θεσσαλονίκης.

Από τα μουσεία μπορείς να πληροφορηθείς για πολλά και να μάθεις. Ένα από τα μουσεία είναι το Παιδικό Μουσείο που περιέχει παιχνίδια από πολλές περιοχές και εκτός Ελλάδας : τσίγκινα, κουρδιστά, κούκλες όπως επίσης και επιτραπέζια, βιβλία. Επίσης εκεί γίνονται διάφορες δράσεις και hands οn δραστηριότητες. Αυτό το μουσείο το προτείνω σε όλα τα παιδιά από 5-8 χρονών αλλά πιστεύω πως και στους συμμαθητές μου θα τους άρεσε.

Figure1 Εβραϊκό Μουσείο Θ.

Figure2 Παιδικό Μουσείο Θ.

Άλλο ένα μουσείο που προτείνω στους συμμαθητές μου είναι το Εβραϊκό μουσείο που έχει ετοιμάσει και παρουσιάσει σημαντικές περιοδικές εκθέσεις. Έχει και την Αίθουσα των Θυμάτων με ονόματα 27.000 πιστοποιημένων Θεσσαλονικέων νεκρών του Ολοκαυτώματος.

Όταν επισκεφτούμε τη Θεσσαλονίκη πιστεύω ότι θα περάσουμε πολύ ωραία και θα μάθουμε πολλά πράγματα.

Τσαρούχης Χ.

Τσουκαλάς Π.

Τη Δευτέρα 7 Απριλίου 2025, οι μαθητές και οι μαθήτριες του τμήματος Γ3 είχαν την ευκαιρία να παρακολουθήσουν μια ενδιαφέρουσα παρουσίαση, με τίτλο «Η σχολική ζωή κάποτε…» από την εξαίρετη φιλόλογο κ. Νικάνδρα Μπακογεώργου, η οποία υπηρέτησε για πολλά χρόνια στο Γενικό Λύκειο Καρπενησίου.

Η εκδήλωση πραγματοποιήθηκε στο πλαίσιο της δράσης με τίτλο «Flashback», που υλοποιείται φέτος στο 1^ο Γυμνάσιο Καρπενησίου, με υπεύθυνους καθηγητές την κ. Μ. Αρμάγου (Μαθηματικό) και τον κ. Ν. Καγιάρα (Φυσικό).

Η παρουσίαση έδωσε στους μαθητές μια μοναδική ευκαιρία να μάθουν για τα πρώτα χρόνια λειτουργίας του σχολείου, τις σημαντικές στιγμές που διαμόρφωσαν την πορεία του, καθώς και για τις αλλαγές που έλαβαν χώρα με την πάροδο του χρόνου. Η δράση αυτή θεωρούμε ότι ενίσχυσε τη σύνδεση των μαθητών με την ιστορική τους κληρονομιά και τους βοήθησε να κατανοήσουν καλύτερα τη σημασία του σχολείου τόσο για κάθε μαθητή προσωπικά, όσο και για την τοπική κοινωνία.

Η τριγωνομετρία είναι ένας κλάδος των μαθηματικών που ασχολείται με τη μελέτη συναρτήσεων που αφορούν στις γωνίες. Οι συναρτήσεις αυτές, που είναι γνωστές ως τριγωνομετρικοί αριθμοί, έχουν πολυάριθμες χρήσεις και καλύπτουν διάφορες περιοχές της επιστήμης και της καθημερινής ζωής. Ενδεικτικά, οι τριγωνομετρικοί αριθμοί αξιοποιούνται στην ανάλυση και επίλυση προβλημάτων γεωμετρίας, φυσικής, μηχανικής, γεωγραφίας, αστρονομίας, αλλά και στη δημιουργία ψηφιακών εικόνων και στην ανάλυση ήχου.

Αν και ο όρος τριγωνομετρία καθιερώθηκε το 1595 από τον Γερμανό μαθηματικό Bartholomäus Pitiscus, οι πρώτες τριγωνομετρικές έννοιες προέκυψαν από παρατηρήσεις των αρχαίων αστρονόμων. Καθώς οι απευθείας μετρήσεις των αποστάσεων μεταξύ των πλανητών ήταν αδύνατες, οι αστρονόμοι χρησιμοποιούσαν τις γωνίες στους υπολογισμούς τους. Ο Ίππαρχος, που θεωρείται ο θεμελιωτής της τριγωνομετρίας, δημιούργησε πίνακες που ανέφεραν τιμές για τις τριγωνομετρικές συναρτήσεις, οι οποίοι συνέβαλαν στην ανάπτυξη της αστρονομίας και της ναυσιπλοΐας. Τέλος, υπάρχουν τεκμήρια που αποδεικνύουν ότι οι αρχαίοι Αιγύπτιοι, Βαβυλώνιοι, Ινδοί και Κινέζοι ασχολήθηκαν ιδιαίτερα με τη μελέτη των γωνιών, συμβάλλοντας στην ανάπτυξη τριγωνομετρικών εννοιών.

Οι μαθητές έρχονται πρώτη φορά σε επαφή με την τριγωνομετρία στη Β γυμνασίου, όπου και ορίζονται οι τριγωνομετρικοί αριθμοί για οξείες γωνίες. Φέτος στα πλαίσια της διδασκαλίας, ομάδα τεσσάρων μαθητριών ανέλαβαν να μελετήσουν την έννοια της εφαπτομένης και να την παρουσιάσουν στην ολομέλεια της τάξης. Στόχος της δραστηριότητας ήταν όλοι οι μαθητές να κατανοήσουν την νέα έννοια με έναν παιγνιώδη, διασκεδαστικό και αλληλεπιδραστικό τρόπο. Για να προσεγγίσουν το θέμα αρχικά οι μαθήτριες κλήθηκαν να συνθέσουν ένα τρισδιάστατο puzzle που απεικονίζει τον Πύργο της Πίζας. Η ενασχόληση των παιδιών με puzzle έχει διάφορα οφέλη. Συμβάλει στην ανάπτυξη της συγκέντρωσής τους και ενισχύει τις ικανότητες επίλυσης προβλημάτων. Επίσης, καλλιεργεί την υπομονή και την επιμονή και όταν τα παιδιά εργάζονται σε ομάδες ενισχύει διάφορες κοινωνικές δεξιότητες.

Εικόνα 1: Σύνθεση puzzle από τις μαθήτριες

Εικόνα 2: Τελική εικόνα puzzle

Στη συνέχεια οι μαθήτριες συνέλεξαν πληροφορίες σχετικές με τον Πύργο της Πίζας που είναι μια ιδιαίτερα  φημισμένη  κατασκευή. Αποτελεί καμπαναριό του καθεδρικού ναού της πόλης και χτίστηκε μεταξύ 1173 και 1372. Ο πύργος είναι παγκοσμίως γνωστός λόγω της κλίσης (περίπου 4 μοιρών) που παρουσιάζει.  Εξαιτίας αυτής της κλίσης είναι ένα εξαιρετικό παράδειγμα που μπορεί να χρησιμοποιηθεί για να εξηγήσει στους μαθητές την έννοια της εφαπτομένης.

Τέλος, οι μαθήτριες χρησιμοποιώντας μια κλωστή σαν νήμα της στάθμης, μέτρησαν τις αποστάσεις που χρειάζονταν για να υπολογίσουν την κλίση του ομοιώματος, ώστε να την συγκρίνουν με αυτή που βρήκαν στις πληροφορίες. Για να συγκριθεί η πραγματική κλίση με αυτή που προέκυψε από τους υπολογισμούς αξιοποιήθηκε εφαρμογή που σχεδιάστηκε στο λογισμικό geogebra.

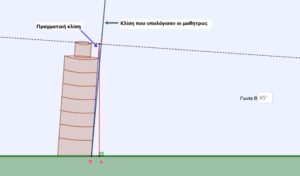
Εικόνα 3: Εφαρμογή σε περιβάλλον Geogebra

Αν και οι μετρήσεις των μαθητριών έδωσαν αποτελέσματα πολύ κοντά στα πραγματικά, συζητήθηκαν ποιοι θα μπορούσαν να είναι οι πιθανοί λόγοι για οποιεσδήποτε αποκλίσεις.

Μια δεύτερη ομάδα που αποτελούνταν από τρεις μαθητές κλήθηκαν να κατασκευάσουν μια τριγωνομετρική υπολογιστική μηχανή, αξιοποιώντας απλά υλικά. Χρησιμοποιώντας ένα κομμάτι μακετόχαρτου, λίγο τετραγωνισμένο χαρτί, ένα δείκτη ρολογιού και ένα διπλόκαρφο κατασκεύασαν μια μηχανή που υπολογίζει το ημίτονο και το συνημίτονο μιας οξείας γωνίας.

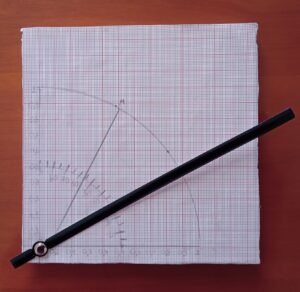
Εικόνα 4: Κατασκευή τριγωνομετρικής υπολογιστικής μηχανής

Στην κατασκευή που έκαναν, ο χρήστης έχει τη δυνατότητα να περιστρέψει τον δείκτη του ρολογιού, έτσι ώστε να σχηματίζει με τον οριζόντιο άξονα οξεία γωνία της επιλογής του. Πάνω στον δείκτη σε απόσταση 10 εκατοστών οι μαθητές θεώρησαν σημείο Μ. Στη συνέχεια κλήθηκαν να συγκρίνουν το ημίτονο και το συνημίτονο της γωνίας με τους δύο αριθμούς που αντιστοιχούν στις συντεταγμένες του Μ. Διαπίστωσαν ότι η προβολή του σημείου στον οριζόντιο άξονα αντιστοιχεί στο συνημίτονο, ενώ η προβολή στον κατακόρυφο άξονα αντιστοιχεί στο ημίτονο  της γωνίας. Στην ολομέλεια της τάξης συζητήθηκε γιατί συμβαίνει αυτό. Εκεί οι μαθητές είχαν τη δυνατότητα να πειραματιστούν και με τη ψηφιακή εκδοχή της μηχανής τους που κατασκευάστηκε στο geogebra.

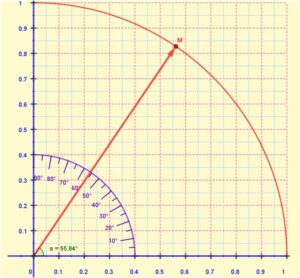
Εικόνα 5: Εφαρμογή σε περιβάλλον Geogebra

Η ίδια κατασκευή ανατέθηκε και σε μαθητής της Γ τάξη διευρύνοντας το πεδίο εφαρμογής. Αυτή η κατασκευή μπορεί να αξιοποιηθεί στη διδασκαλία των σχέσεων που συνδέουν τους τριγωνομετρικούς αριθμούς παραπληρωματικών γωνιών.

Εικόνα 6: Κατασκευή τριγωνομετρικής υπολογιστικής μηχανής

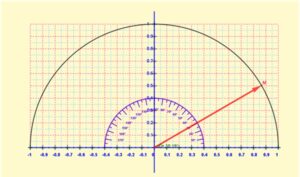
Εικόνα 7: Εφαρμογή σε περιβάλλον Geogebra