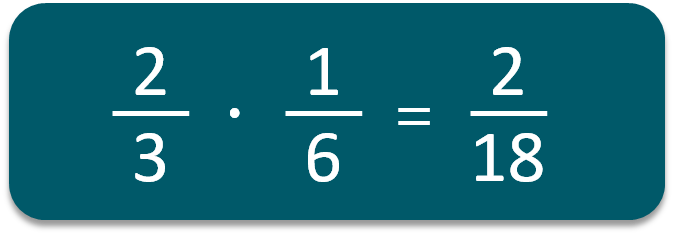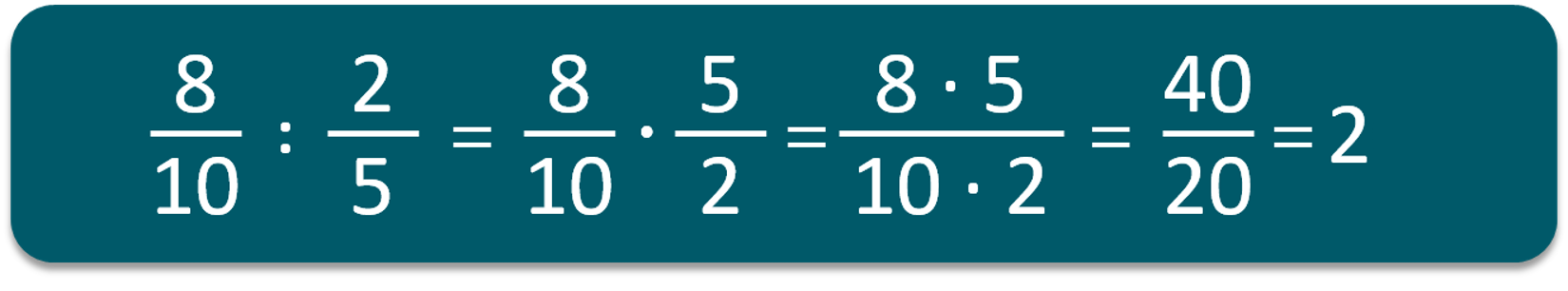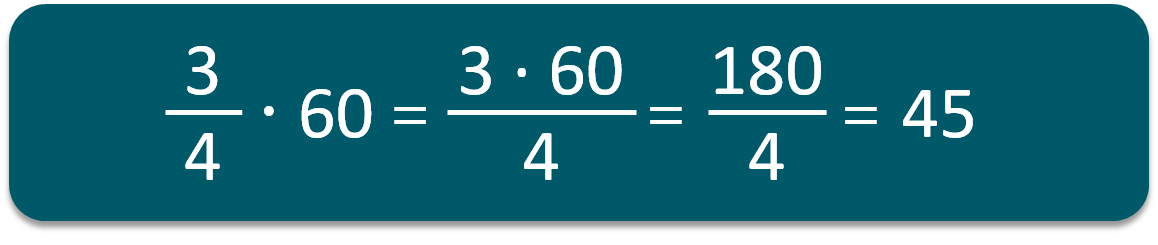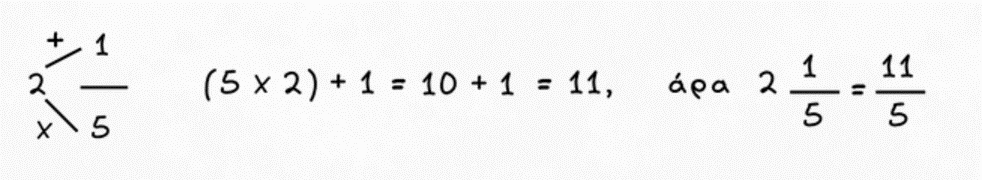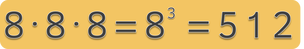











Αριθμητικό μοτίβο
Σε μια σειρά αριθμών που υπάρχει μια σχέση σταθερή και επαναλαμβανόμενη ανάμεσα στους αριθμούς, ο κανόνας που ορίζει τη σχέση αυτή και μας δείχνει πώς δημιουργήθηκε η σειρά των αριθμών λέγεται αριθμητικό μοτίβο. (π.χ. 5, 10, 15, 20, 25, … α, α+5)
Αυτή τη διαδοχή των αριθμών τη λέμε ακολουθία και κάθε αριθμός λέγεται όρος της ακολουθίας.
Για να Δημιουργήσω απλά γεωμετρικά μοτίβα θα πρέπει να :
- αναγνωρίζω τα γεωμετρικά σχήματα που το συνθέτουν
- κατανοήσω ότι επαναλαμβάνεται ένα μέρος του
- εντοπίσω την αλλαγή και να συνεχίσω τη σειρά.





Κεφάλαιο , τόκος , επιτόκιο.
Τα χρήματα που κάποιος καταθέτει σε τράπεζα ή δανείζεται από την τράπεζα λέγονται κεφάλαιο.
Όταν μας δανείζει χρήματα η τράπεζα, πληρώνουμε ένα ποσό επιπλέον αυτών που δανειστήκαμε –ο τόκος – , το οποίο είναι ένα ποσοστό του χρηματικού ποσού που δανειστήκαμε.
Η τράπεζα το υπολογίζει σύμφωνα με ένα ποσοστό στα 100 – επιτόκιο – που έχει ορίσει για αμοιβή.
Αντίθετα, όταν εμείς καταθέτουμε χρήματα στην τράπεζα, τότε η τράπεζα πληρώνει τόκο σε εμάς (που τον υπολογίζει πάλι σύμφωνα με κάποιο επιτόκιο).
Πρόβλημα:
Ο Δημήτρης πήρε δάνειο από την τράπεζα για να αγοράσει αυτοκίνητο. Η αξία του δανείου ήταν 20.000 € με επιτόκιο 8 % το χρόνο . Πόσο θα πληρώσει έπειτα από ένα χρόνο ;
Απάντηση: Θα πληρώσει 1600 € για τόκους , επομένως συνολικά
20000 + 1600 = 21600 €
Σε ένα χρόνο θα πληρώσω 5 € τόκο και συνολικά 100 + 5 = 105€
Καταθέτω 100 € με επιτόκιο 2%.
Σε ένα χρόνο θα πάρω 2 € τόκο και συνολικά 100 + 2 = 102€


Όταν θέλουμε να μετατρέψουμε μια μονάδα μήκους από μεγαλύτερη σε μικρότερη κάνουμε πολλαπλασιασμό με το 10 (μία σκάλα), το 100(δύο σκάλες) ή το 1000 (τρεις σκάλες).
Θέλω να μετατρέψω 3 μέτρα σε δεκατόμετρα: 3 μ. = ___ δεκ.
Σκέφτομαι: Θέλω να πάω από τα μέτρα στα δέκατα.
Άρα ακολουθώ τα βελάκια και κάνω ένα πηδηματάκι κάτω .
Λέω 3 x 10 = 30. Συνεπώς 3μ. = 30 δεκ.
Θέλω να μετατρέψω 3 μέτρα σε εκατοστά: 3 μ. = _____ εκ.
Σκέφτομαι: Θέλω να πάω από τα μέτρα στα εκατοστά.
Άρα ακολουθώ τα βελάκια και κάνω δύο πηδηματάκια κάτω.
Λέω 3 x 10 =30 και 30 x 10 = 300 (ή 3 x 100 =300). Συνεπώς 3μ. = 300 εκ.
Αντίθετα, όταν θέλουμε να μετατρέψουμε μια μονάδα μήκους από μικρότερη σε μεγαλύτερη κάνουμε διαίρεση με το 10 (μία σκάλα), το 100 (δύο σκάλες) ή το 1000 (τρεις σκάλες). Για παράδειγμα:
Θέλω να μετατρέψω 300 εκατοστά σε δέκατα: 300 εκ. = _____ δεκ.
Σκέφτομαι: Θέλω να πάω από τα εκατοστά στα δέκατα.
Άρα ακολουθώ τα βελάκια και κάνω ένα πηδηματάκι πάνω.
Λέω 300 : 10 = 30. Συνεπώς 300 εκ. = 30 δεκ.
Θέλω να μετατρέψω 4.000 χιλιοστά σε μέτρα: 4.000 χιλ. = _____ μ.
Σκέφτομαι: Θέλω να πάω από τα χιλιοστά στα μέτρα.
Άρα ακολουθώ τα βελάκια και κάνω τρία πηδηματάκια πάνω.
Λέω 4.000 : 10 = 400 και 400 : 10 = 40 και 40 : 10 =4 (ή 4.000 : 1.000 = 4).
Συνεπώς 4.000 χιλ. = 4 μ.

Πολλές φορές μας δίνουν πολλά δεδομένα και θέλουμε να τα εκφράσουμε μόνο με μια τιμή.Τότε βρίσκουμε στο μέσο όρο ή αλλιώς τη μέση τιμή).
π.χ. Οι μπασκετμπολίστες του Ολυμπιακού έχουν τις εξής ηλικίες:
Παπαλουκάς 32 ετών,
Σχορτσιανίτης 25 ετών,
Τσίλντρες 25 ετών,
Μπουρούσης 23 ετών και
Βούισιτς 28 ετών.
Θέλω να εκφράσω αυτές τις ηλικίες με έναν μόνο αριθμό. Τότε θα πρέπει να βρω τον μέσο όρο των παραπάνω ηλικιών.
Για να βρω τον μέσο όρο, προσθέτω τους αριθμούς που μας έχουν δώσει και διαιρούμε το άθροισμά τους με τον αριθμό που δηλώνει το πλήθος τους.
π.χ. 32 + 25 + 25 + 23 + 28 = 133 είναι το άθροισμα των ηλικιών τους.
Οι παίκτες είναι 5
άρα : 133 : 5 = 26,6 έτη είναι ο μέσος όρος των παικτών του Ολυμπιακού.
Ο μέσος όρος πολλές φορές δεν συμπίπτει (δεν είναι ίδιος) με κάποιον από τους αριθμούς που χρησιμοποιήσαμε ως δεδομένα.











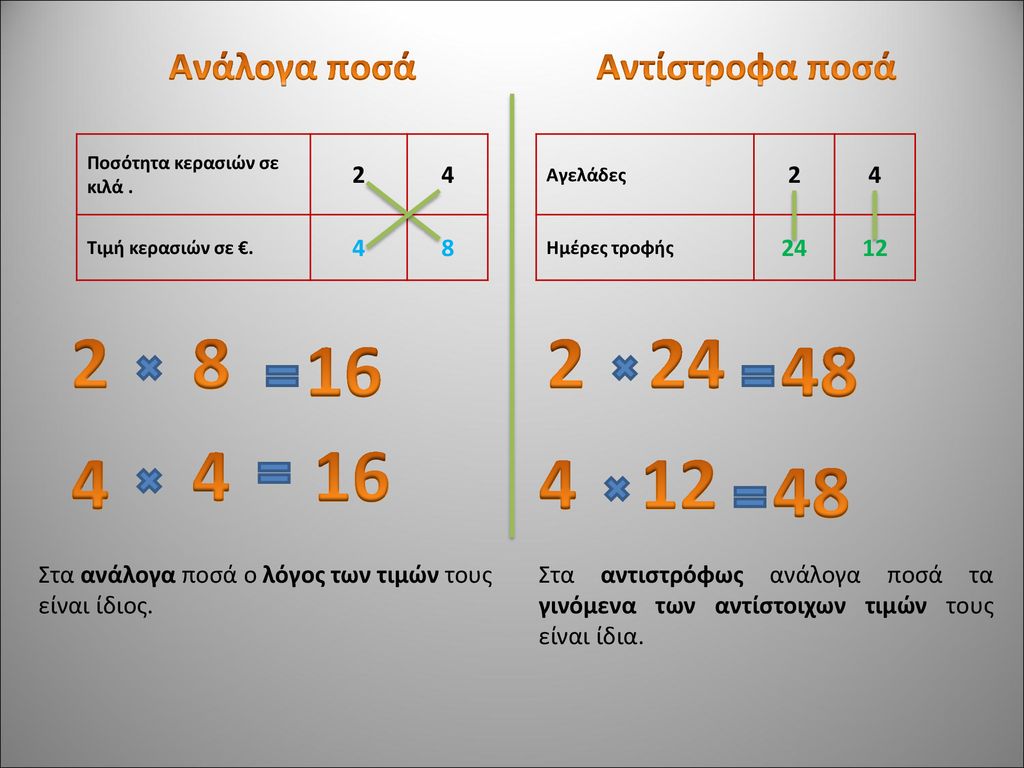
Δύο ποσά είναι ανάλογα, όταν οι τιμές του ενός προκύπτουν από τις τιμές του άλλου, πολλαπλασιάζοντας κάθε φορά με έναν σταθερό αριθμό. Για παράδειγμα, η αξία των τετραδίων που αγοράζουμε είναι ανάλογη προς το πλήθος των τετραδίων:
κάθε φορά για να βρούμε την αξία των τετραδίων πολλαπλασιάζουμε το πλήθος των τετραδίων με τον ίδιο αριθμό δηλαδή το 3 .
Στα ανάλογα ποσά ο λόγος των τιμών των δύο ποσών είναι σταθερός : 1/3 = 2/6 = 3/9 = 4/12
Στα ανάλογα ποσά, όταν πολλαπλασιάζεται η τιμή του ενός ποσού με έναν αριθμό, τότε πολλαπλασιάζεται και η τιμή του άλλου ποσού με τον ίδιο αριθμό.



- Ο διαιρετέος είναι ο αριθμός που θα διαιρεθεί.
- Ο διαιρέτης είναι ο αριθμός που δείχνει σε πόσα ίσα μέρη θα χωριστεί ο διαιρετέος.
- Το πηλίκο (το αποτέλεσμα της διαίρεσης) δείχνει πόσο μεγάλο είναι κάθε ένα από τα ίσα μέρη στα οποία χωρίστηκε ο διαιρετέος.

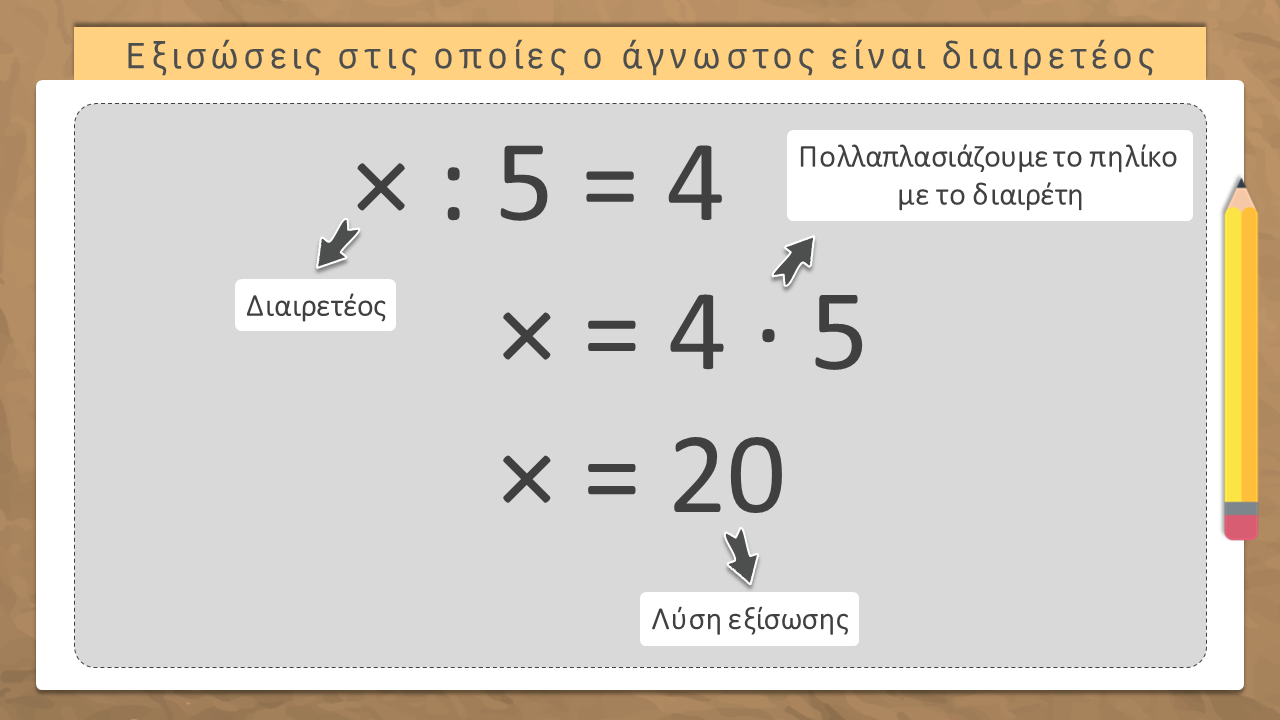
- Όταν ο άγνωστος είναι διαιρετέος, για να λύσουμε την εξίσωση πολλαπλασιάζουμε το πηλίκο με τον διαιρέτη.

- Όταν ο άγνωστος είναι διαιρέτης, για να λύσουμε την εξίσωση διαιρούμε τον διαιρετέο με το πηλίκο.


- Για να λύσουμε μια εξίσωση στην οποία ο άγνωστος είναι παράγοντας γινομένου, διαιρούμε το γινόμενο με τον άλλο παράγοντα.
- Διαιρέτη βάζω πάντα τον αριθμό που είναι μαζί με το X και διαιρετέο το γινόμενο.

Χ = 192 : 24
Χ = 8
- Όταν σε μια εξίσωση ψάχνω κάποιον από τους δυο παράγοντες του πολλαπλασιασμού κάνω διαίρεση.
- Για να κάνω διαίρεση με κλάσματα αντιστρέφω τους όρους του 2ου κλάσματος και αντί για διαίρεση κάνω πολλαπλασιασμό.
- Αν κάποιος από τους δυο παράγοντες του πολλαπλασιασμού είναι μεικτός ή ακέραιος και ο άλλος κλάσμα για να κάνω τη διαίρεση πρέπει να τα κάνω όλα κλάσματα.
- Δεν μπορώ να κάνω διαίρεση αν ο διαιρέτης είναι δεκαδικός. Πρέπει να τον κάνω ακέραιο πολλαπλασιάζοντάς τον με το 10, 100, 1000, κ.τ.λ. ανάλογα με τα δεκαδικά του ψηφία. Το ίδιο πρέπει να κάνω και με το διαιρετέο.


Μειωτέος είναι ο αριθμός που μειώνεται. Στην κάθετη αφαίρεση είναι ο επάνω αριθμός, ενώ στην οριζόντια ο πρώτος αριθμός.
Αφαιρετέος είναι ο αριθμός που θα αφαιρεθεί από τον μειωτέο. Στην κάθετη αφαίρεση είναι ο κάτω αριθμός, ενώ στην οριζόντια ο δεύτερος αριθμός.
Το αποτέλεσμα της αφαίρεσης λέγεται διαφορά.
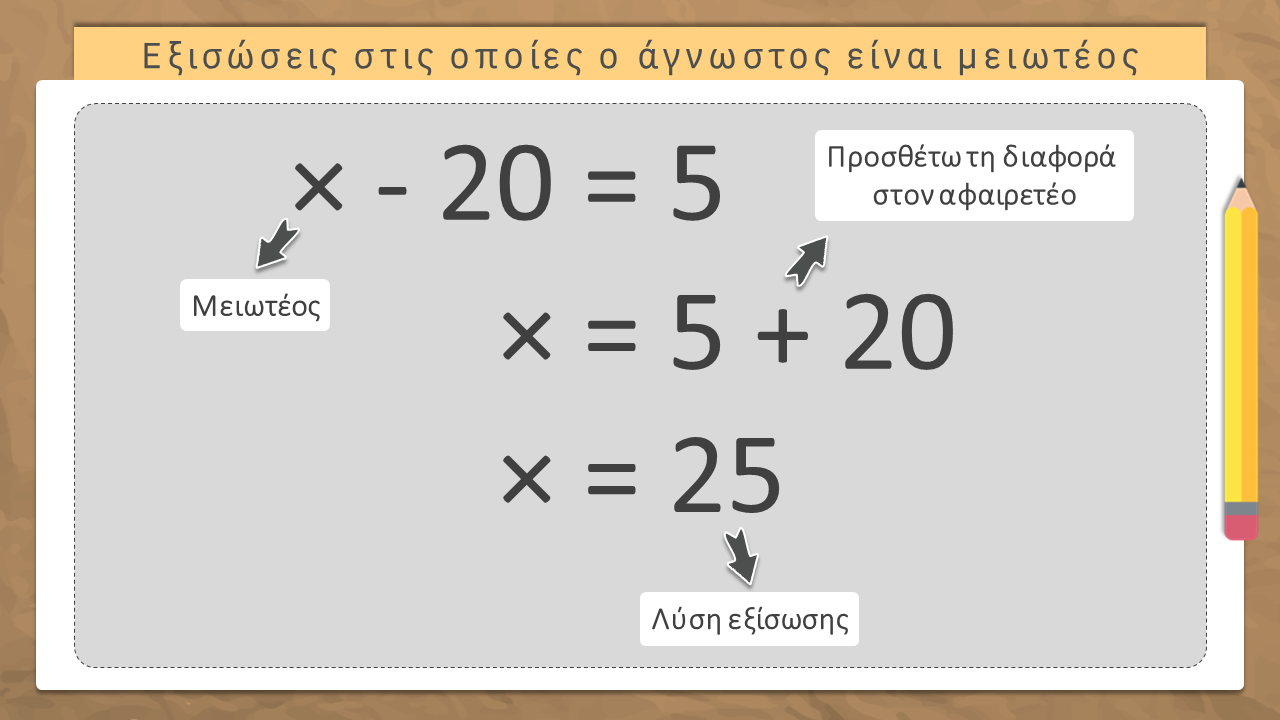
- Όταν ο άγνωστος είναι ο μειωτέος, για να λύσω την εξίσωση προσθέτω στη διαφορά τον αφαιρετέο.
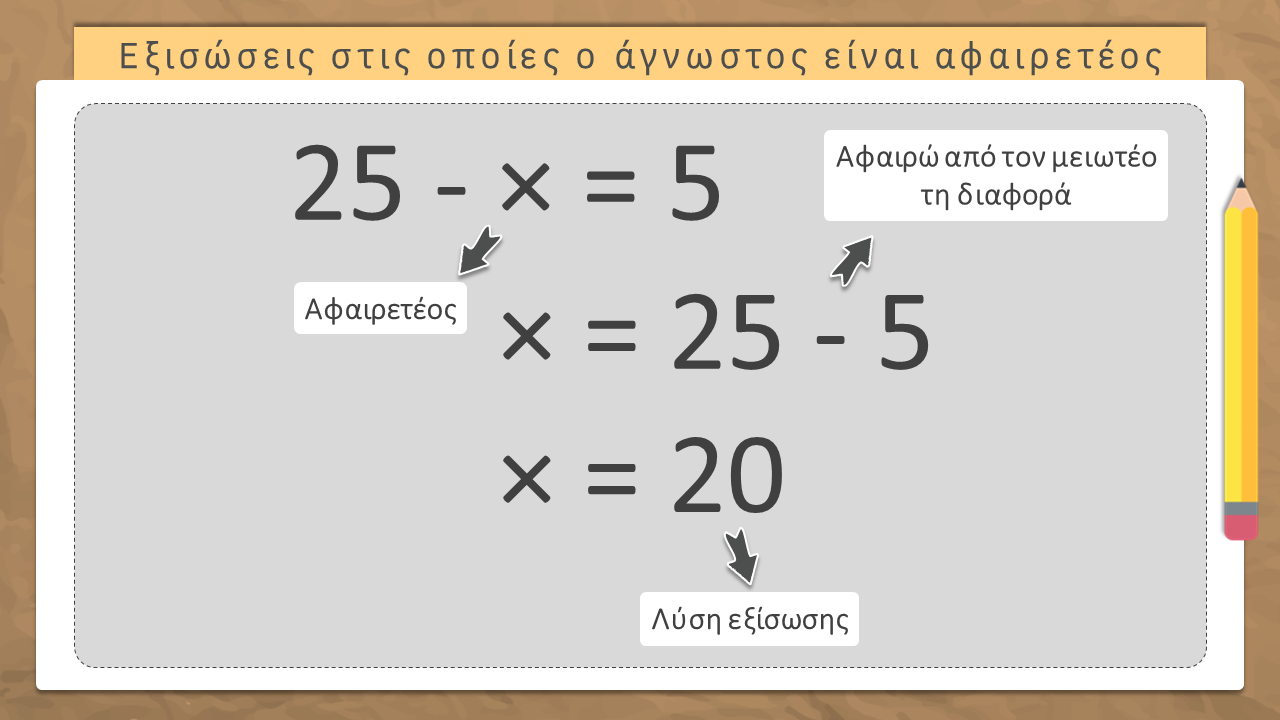
- Όταν ο άγνωστος είναι ο αφαιρετέος, για να λύσω την εξίσωση αφαιρώ από τον μειωτέο τη διαφορά.

- Εξίσωση ονομάζεται μια ισότητα που περιέχει μια μεταβλητή.
- Η τιμή που επαληθεύει την εξίσωση λέγεται λύση της εξίσωσης.
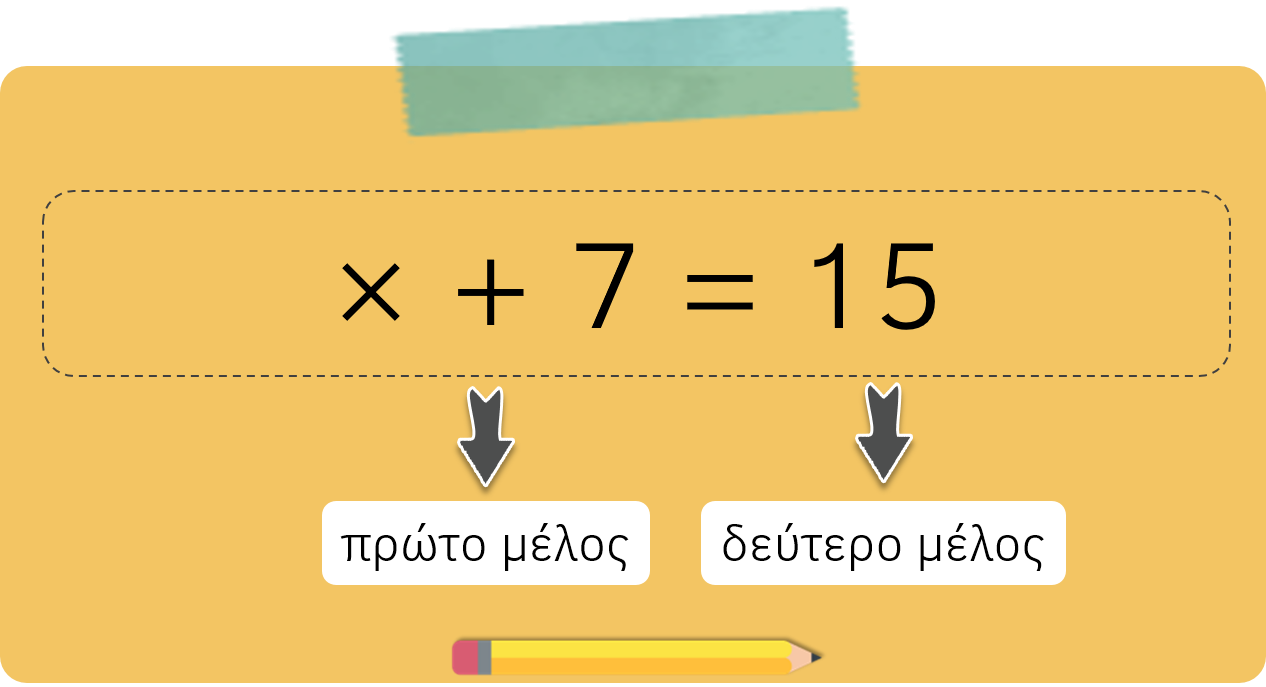
- Οι όροι που βρίσκονται αριστερά του ίσον (=) αποτελούν το πρώτο μέλος (α΄ μέλος) της εξίσωσης και αυτοί που βρίσκονται δεξιά το δεύτερο μέλος (β΄ μέλος).
στην εξίσωση Χ + 7 = 15
η τιμή Χ=8 είναι η λύση, γιατί 8 + 7 = 15

Βήμα 2: Συμβολίζω με μια μεταβλητή την άγνωστη ποσότητα.
Βήμα 3: Εκφράζω με ισότητα (εξίσωση) το πρόβλημα.
Βήμα 4: Λύνω την εξίσωση.
Βήμα 5: Επαληθεύω την εξίσωση.
Μια μεταβλητή είναι ένα γράμμα ή ένα σύμβολο το οποίο χρησιμοποιούμε σε μια αριθμητική παράσταση ή σε ένα πρόβλημα, για να δηλώσουμε έναν αριθμό που είναι άγνωστος και μπορεί να πάρει διάφορες τιμές.
- Το πιο συνηθισμένο γράμμα για το συμβολισμό μιας μεταβλητής στα μαθηματικά είναι το «Χ». Αυτό όμως δεν είναι υποχρεωτικό.
- Μια αριθμητική παράσταση που περιέχει μια μεταβλητή τη λέμε αλγεβρική παράσταση.
- Αν μια φράση περιέχει μια από τις λέξεις “κάποιος”, “ένας”, “μια τιμή”, ή κάποια παρόμοια, τότε γράφουμε στη θέση αυτού του μεγέθους μια μεταβλητή.


|
4. Για να υπολογίσω αριθμητικές παραστάσεις που περιέχουν κλασματικούς αριθμούς, πρώτα μετατρέπω, αν χρειάζεται, κάποιους από τους αριθμούς σε άλλη μορφή. Στην συνέχεια εκτελούμε τις πράξεις από αριστερά προς τα δεξιά, με τη γνωστή σειρά (παρενθέσεις, πολλαπλασιασμοί και διαιρέσεις, προσθέσεις κι αφαιρέσεις).
|
Για να λύσω ένα πρόβλημα που τα δεδομένα του βρίσκονται σε διαφορετικές μορφές (φυσικοί, δεκαδικοί, κλασματικοί, μεικτοί αριθμοί), ακολουθώ τα παρακάτω βήματα:
- 1ο βήμα: Μετρατρέπω όλα τα δεδομένα στην ίδια μορφή.
- 2ο βήμα: Εκτελώ τις πράξεις σύμφωνα με όσα λέει το πρόβλημα.
- 3ο βήμα: Ελέγχω αν το αποτέλεσμα που βρήκα είναι λογικό.
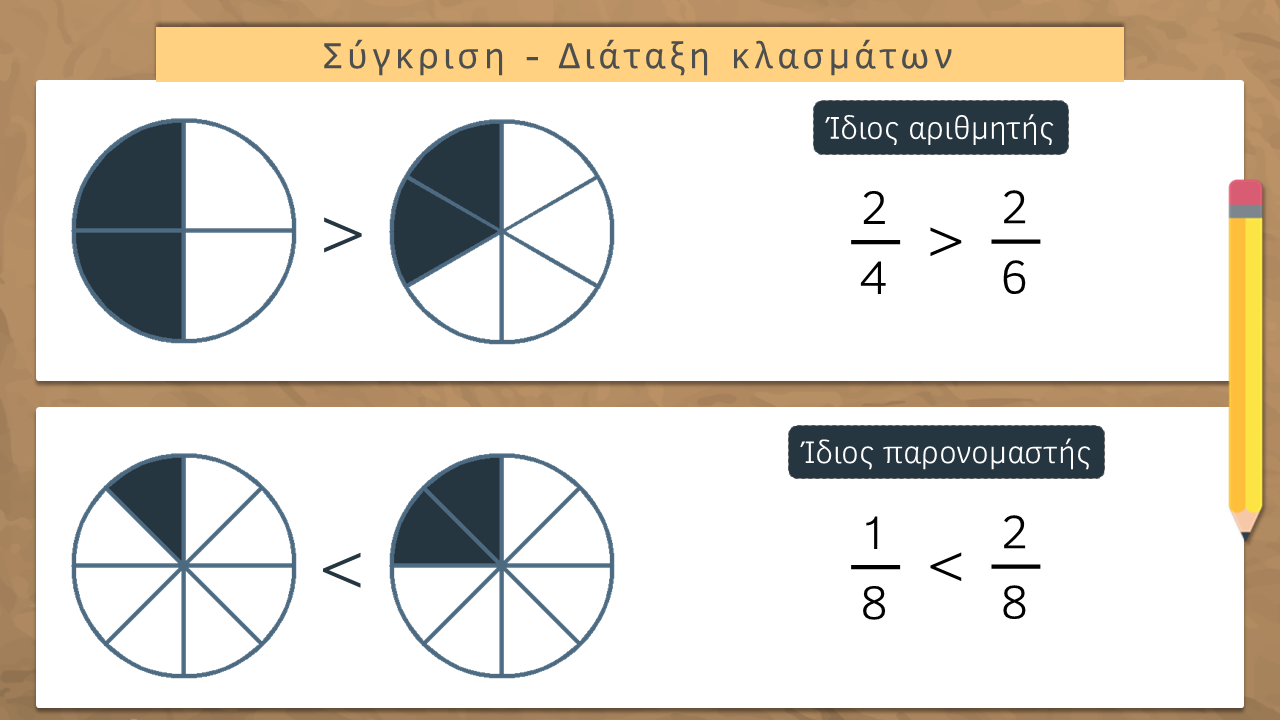
ΣΥΓΚΡΙΣΗ-ΔΙΑΤΑΞΗ ΚΛΑΣΜΑΤΩΝ
- Για να μπορέσω να συγκρίνω δύο ή περισσότερα κλάσματα πρέπει να έχουν τον ίδιο αριθμητή ή τον ίδιο παρονομαστή.
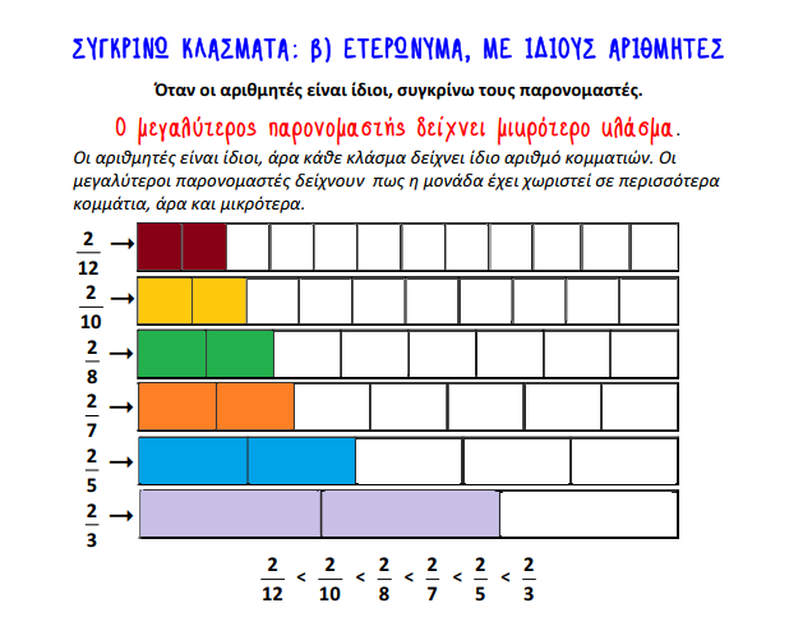

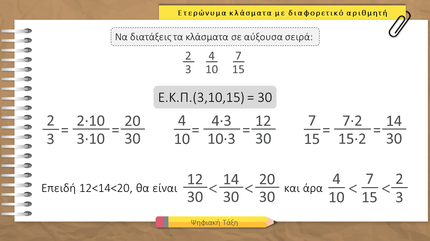
Για να συγκρίνω δύο κλάσματα που έχουν διαφορετικούς και τους αριθμητές και τους παρονομαστές τους, πρέπει να τα κάνω ομώνυμα.
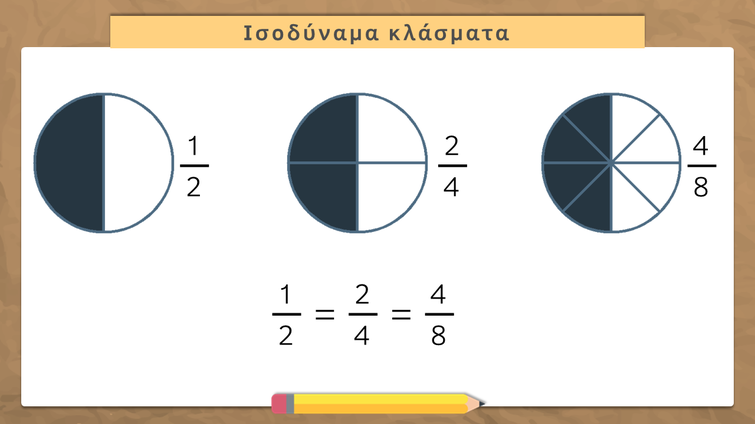
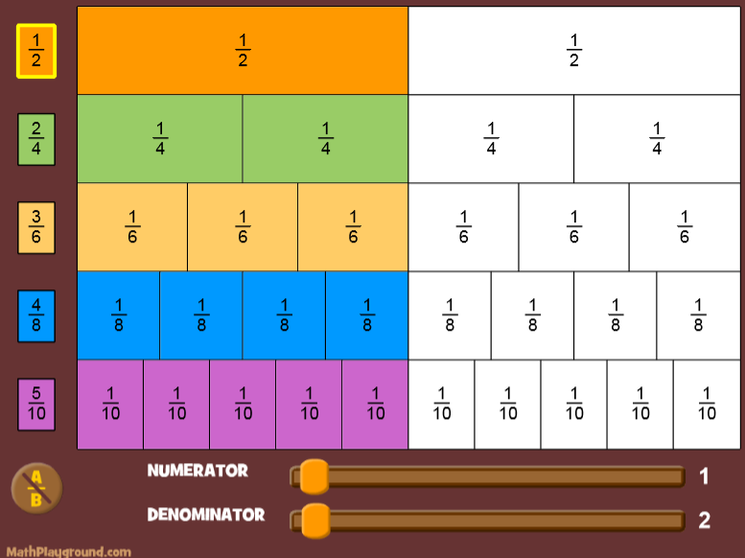
ΙΣΟΔΥΝΑΜΑ ΚΛΑΣΜΑΤΑ
|
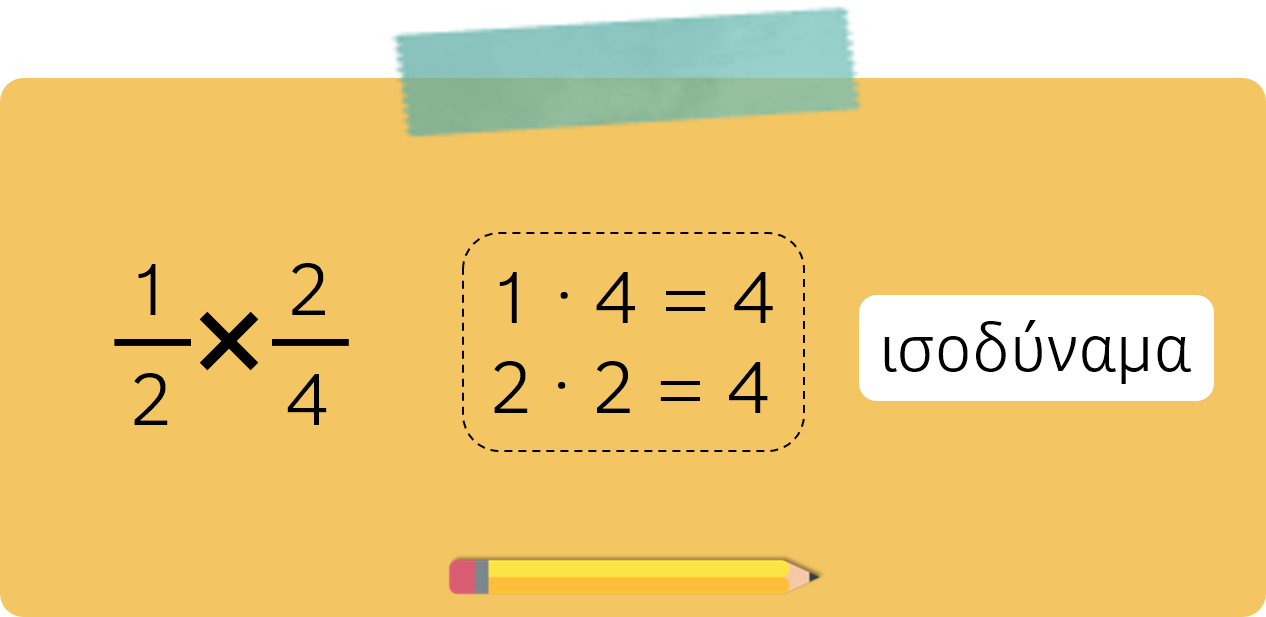
Για να βρούμε αν δύο κλάσματα είναι ισοδύναμα, πολλαπλασιάζουμε τους όρους σταυρωτά (σταυρωτά ή χιαστί γινόμενα).
|
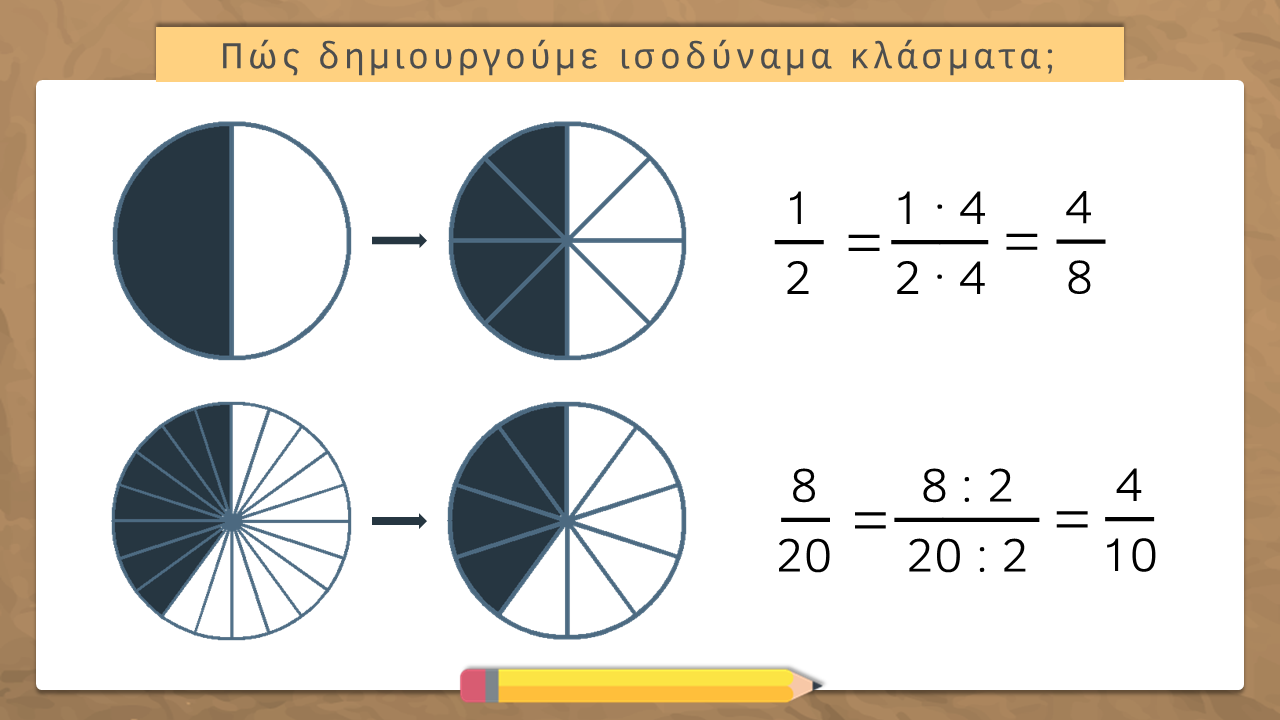
Πώς δημιουργούμε ισοδύναμα κλάσματα;
Η διαδικασία αυτή ονομάζεται απλοποίηση (το κλάσμα γίνεται πιο απλό). |
Για να απλοποιήσω ένα κλάσμα και να το κάνω ανάγωγο, χρησιμοποιώ το Μ.Κ.Δ. με τον οποίο διαιρώ και τους δύο όρους του κλάσματος.
Το κλάσμα ως ακριβές πηλίκο διαίρεσης
- Κάθε κλάσμα είναι ίσο με το πηλίκο μιας διαίρεση: (αριθμητής) : (παρονομαστή)
- Αντίστροφα κάθε διαίρεση μπορούμε να την εκφράσουμε και ως κλάσμα.
- Κάθε κλάσμα μπορεί να εκφραστεί ως δεκαδικός αν κάνουμε τη διαίρεση.
- Αν η διαίρεση είναι ατελής σταματάμε όπου μας χρειάζεται.
- Κάθε δεκαδικός μπορεί να μετατραπεί σε κλάσμα.
|
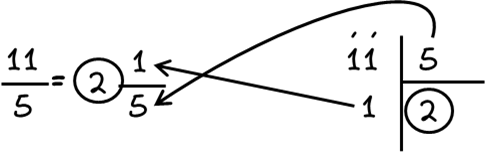
1.Διαιρούμε τον αριθμητή με τον παρονομαστή. 2. Το πηλίκο της διαίρεσης είναι ο ακέραιος του μεικτού. 3. Το κλάσμα του μεικτού έχει αριθμητή το υπόλοιπο της διαίρεσης και παρονομαστή τον ίδιο με το αρχικό κλάσμα. |
1. Πολλαπλασιάζουμε τον ακέραιο του μεικτού με τον παρονομαστή του κλάσματός του.
2. Στο γινόμενο που προκύπτει προσθέτουμε τον αριθμητή του μεικτού αριθμού.
3. Το αποτέλεσμα αποτελεί τον αριθμητή του νέου κλάσματος, ενώ παρονομαστής παραμένει ο ίδιος.
|
Κλάσμα είναι ο αριθμός που μας δείχνει σε πόσα ίσα μέρη χωρίσαμε την ακέραια μονάδα και πόσα από αυτά πήραμε.
Κάθε κλάσμα έχει:
|
Θυμάμαι ότι:
- Όταν ο αριθμητής είναι η μονάδα (το 1) και παρονομαστής οποιοσδήποτε αριθμός π.χ. 1/3 τότε το κλάσμα λέγεται κλασματική μονάδα.
- Ένα κλάσμα είναι ίσο με την ακέραια μονάδα, όταν έχει τον αριθμητή ίσο με τον παρονομαστή π.χ. 4/4.
- Όταν ο αριθμητής είναι μικρότερος του παρονομαστή π.χ. 2/5 τότε το κλάσμα λέγεται γνήσιο.
- Όταν ο αριθμητής είναι μεγαλύτερος από τον παρονομαστή π.χ. 5/2 τότε το κλάσμα λέγεται καταχρηστικό.
- Μεικτός αριθμός είναι αυτός που αποτελείται από ακέραιο και κλασματικό μέρος π.χ. 4 1/2.
Ετερώνυμα λέγονται τα κλάσματα που έχουνε διαφορετικούς παρονομαστές.
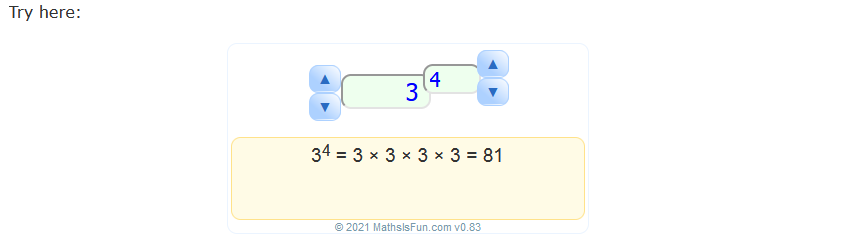
ΔΥΝΑΜΕΙΣ


ΔΗΜΙΟΥΡΓΗΣΤΕ ΔΥΝΑΜΕΙΣ
ΠΟΛΛΑΠΛΑΣΙΑ ΕΝΟΣ ΑΡΙΘΜΟΥ- Ε.Κ.Π.
Πολλαπλάσια ενός αριθμού – Ε.Κ.Π.
|
Πολλαπλάσια ενός αριθμού είναι οι αριθμοί που προκύπτουν (δημιουργούνται) όταν πολλαπλασιάσουμε το συγκεκριμένο αριθμό με οποιοδήποτε ακέραιο αριθμό.
Παράδειγμα:
Τα πολλαπλάσια του 4 είναι το 4, 8, 12, 16… 4×2=8, 4×3=12, 4×4=16 Τα πολλαπλάσια κάθε αριθμού είναι άπειρα, διότι άπειροι είναι και οι αριθμοί με τους οποίους μπορώ να τον πολλαπλασιάσω.
|
Κοινά πολλαπλάσια (Κ.Π.) δύο ή περισσότερων αριθμών είναι τα πολλαπλάσια τα οποία είναι ίδια σε όλους τους αριθμούς
Παράδειγμα:
Π3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, … Π4 = 4, 8, 12, 16, 20, 24, 28, … Π6 = 6, 12, 18, 24, 30, … Τα κοινά πολλαπλάσια του 3 του 4 και του 6, που είναι μικρότερα από το 30, είναι τα 12, 24.
|
Πώς βρίσκουμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών
1ος ΤΡΟΠΟΣ

- Βρίσκουμε μερικά πολλαπλάσια των αριθμών.
- Σημειώνουμε τα κοινά πολλαπλάσιά τους.
- Επιλέγουμε το μικρότερο από αυτά.
2ος ΤΡΟΠΟΣ

Παίρνουμε τον μεγαλύτερο αριθμό. Εξετάζουμε αν είναι πολλαπλάσιο ταυτόχρονα των άλλων. Εάν είναι, αυτός είναι και το Ε.Κ.Π.
Εάν δεν είναι, παίρνουμε τον διπλάσιό του και εξετάζουμε το ίδιο πράγμα.
Εάν δεν είναι και πάλι πολλαπλάσιο των άλλων, παίρνουμε τον τριπλάσιό του και ελέγχουμε ξανά. Συνεχίζουμε με τον ίδιο τρόπο, μέχρι να βρούμε ένα πολλαπλάσιο του μεγαλύτερου αριθμού που να είναι πολλαπλάσιο ταυτόχρονα και των άλλων αριθμών. Αυτό θα είναι και το Ε.Κ.Π.
3ος ΤΡΟΠΟΣ

- Γράφω οριζόντια τους αριθμούς και δεξιά τους φέρνω μια κατακόρυφη γραμμή.
- Δεξιά της γραμμής γράφω πρώτους αριθμούς (2,3,5,7,11…) που διαιρούν έστω και έναν από τους αριθμούς που έχουν δοθεί.
- Τότε αριστερά της γραμμής, κάτω από τους αριθμούς που έχουν δοθεί, βάζω τα πηλίκα (όταν η διαίρεση είναι τέλεια) ή τον ίδιο αριθμό (όταν η διαίρεση δεν είναι τέλεια).
- Συνεχίζω την ίδια διαδικασία μέχρι όλα τα πηλίκα να γίνουν 1.
- Έτσι καταλήγουμε σε μια νέα γραμμή που όλα τα πηλίκα είναι μονάδες. Το Ε.Κ.Π. είναι το γινόμενο των αριθμών που βρίσκονται δεξιά της κατακόρυφης γραμμής
ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ


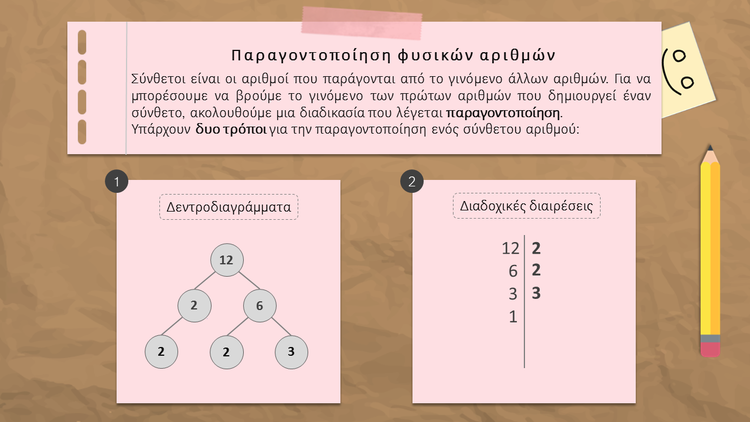
Δεντροδιάγραμμα
Γράφουμε το γινόμενο που μας δίνει τον αριθμό 12. Εδώ γράψαμε 2 Χ 6.
Ο αριθμός 2 είναι πρώτος, οπότε συνεχίζουμε τη διαδικασία για τον αριθμό 6, του οποίου το γινόμενο είναι 2 Χ 3.
Στην τρίτη σειρά γράφουμε τον αριθμό 2 και το γινόμενο 2 Χ 3.
Η ανάλυση τελειώνει, όταν όλοι οι παράγοντες είναι πρώτοι αριθμοί όπως εδώ (2, 2 και 3).
Άρα ο αριθμός 12 μπορεί να εκφραστεί ως γινόμενο πρώτων παραγόντων ως εξής: 12 = 2 Χ 2 Χ 3
Διαδοχικές διαιρέσεις
|
1. Εξετάζουμε ποιος είναι ο μικρότερος πρώτος αριθμός που διαιρεί ακριβώς το 12. Είναι το 2. Διαιρούμε με το 2 και γράφουμε κάτω από το 6 το πηλίκο της διαίρεσης.
2. Συνεχίζουμε την ίδια διαδικασία για το 6. Διαιρούμε με το 2 και γράφουμε το πηλίκο της διαίρεσης που είναι το 3. 3. Το 3 δε διαιρείται με το 2. Πάμε στον επόμενο πρώτο αριθμό που είναι το 3 και εξετάζουμε αν διαιρείται με το 3. Διαιρούμε με το 3 και γράφουμε το πηλίκο της διαίρεσης που είναι το 1. 4. Αν το πηλίκο είναι η μονάδα τότε τελειώνει και η ανάλυση. Άρα ο αριθμός 12 εκφράζεται ως γινόμενο πρώτων παραγόντων ως εξής: 12 = 2 Χ 2 Χ 3 |
- Ο αριθμός 60 γράφεται: 2 Χ 2 Χ 3 Χ 5
- Ο αριθμός 91 (πρώτος αριθμός) μπορεί να γραφτεί ως 1 Χ 91
ΠΡΩΤΟΙ ΚΑΙ ΣΥΝΘΕΤΟΙ ΑΡΙΘΜΟΙ
Πρώτος λέγεται οποιοσδήποτε αριθμός που έχει μόνο δύο διαιρέτες: το 1 και τον εαυτό του.
Σύνθετος λέγεται κάθε αριθμός που εκτός από τον εαυτό του και το 1, έχει και άλλους διαιρέτες.
Το 7 είναι πρώτος αριθμός (οι διαιρέτες του είναι μόνο το 1 και το 7).
Το 4 είναι σύνθετος αριθμός (οι διαιρέτες του είναι: 1, 2, 4).
Το 24 είναι σύνθετος αριθμός (οι διαιρέτες του είναι: 1, 2, 3, 4, 6, 8, 12, 24).
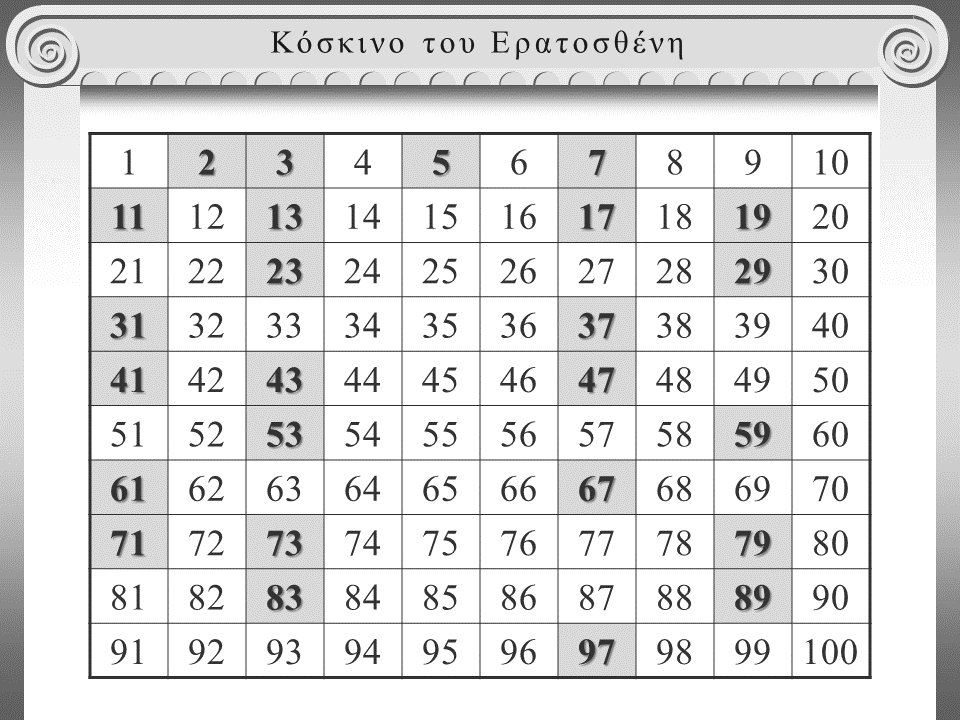
Κόσκινο του Ερατοσθένη
Με την απλή μέθοδο του Ερατοσθένη, γνωστή ως “Κόσκινο του Ερατοσθένη”, που χρησιμοποιείται μέχρι και σήμερα, βρίσκουμε όλους τους πρώτους αριθμούς που είναι μικρότεροι από δοσμένο αριθμό.

Ένας αριθμός διαιρείται με το:
- το 10 όταν τελειώνει σε ένα τουλάχιστον 0
- το 100 όταν τελειώνει σε δύο τουλάχιστον 0
- το 1.000 όταν τελειώνει σε τρία τουλάχιστον 0

Ένας αριθμός διαιρείται με το 9 αν το μονοψήφιο άθροισμα των ψηφίων του είναι το 9.


Ένας αριθμός διαιρείται με το 5 αν το τελευταίο ψηφίο είναι 0 ή 5.


Ένας αριθμός διαιρείται με το 3, αν το μονοψήφιο άθροισμα των ψηφίων του είναι 3, 6 ή 9.

Ένας αριθμός διαιρείται με το 2 αν το τελευταίο ψηφίο είναι άρτιος (ζυγός) αριθμός (0,2,4,6,8).
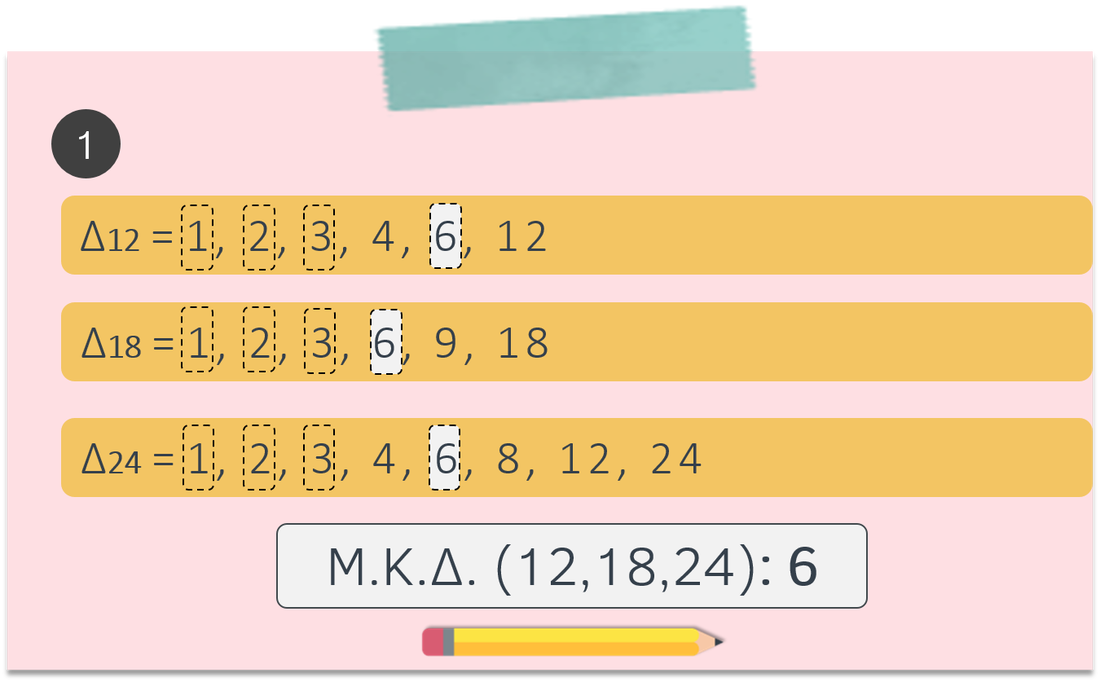
Διαιρέτες ενός αριθμού – Μ.Κ.Δ. Αριθμών
- Όλοι οι φυσικοί αριθμοί έχουν διαιρέτες τουλάχιστον το 1 και τον εαυτό τους.
- Ένας αριθμός μπορεί να έχει πολλούς διαιρέτες.
- Υπάρχουν αριθμοί που κάποιοι από τους διαιρέτες που έχουν είναι ίδιοι. Λέμε τότε ότι έχουν κοινούς διαιρέτες.






Αριθμητική παράσταση είναι μια σειρά πράξεων με αριθμούς.
Μια αριθμητική παράσταση μπορεί να περιλαμβάνει παρενθέσεις, αγκύλες κλπ.


Διαίρεση φυσι
- Κάθε αριθμός αν διαιρεθεί με το 1, δίνει πηλίκο τον εαυτό του.
π.χ. 5 : 1 = 5
- Κάθε αριθμός αν διαιρεθεί με τον εαυτό του δίνει πηλίκο το 1.
π.χ. 9 : 9 = 1
- Το μηδέν (0) με όποιον αριθμό κι αν διαιρεθεί, δίνει πηλίκο τον εαυτό του.
π.χ. 0 : 5 = 0
- Δεν επιτρέπεται να διαιρέσουμε έναν αριθμό δια μηδέν (0).
π.χ. 4 : 0 είναι αδύνατο
- Σε κάθε διαίρεση αν πολλαπλασιάσουμε ή διαιρέσουμε τους δύο όρους με τον ίδιο αριθμό, το πηλίκο δεν αλλάζει.
π.χ. 20 : 4 = 5 (20 • 2) : (4 • 2) = 40 : 8 = 5


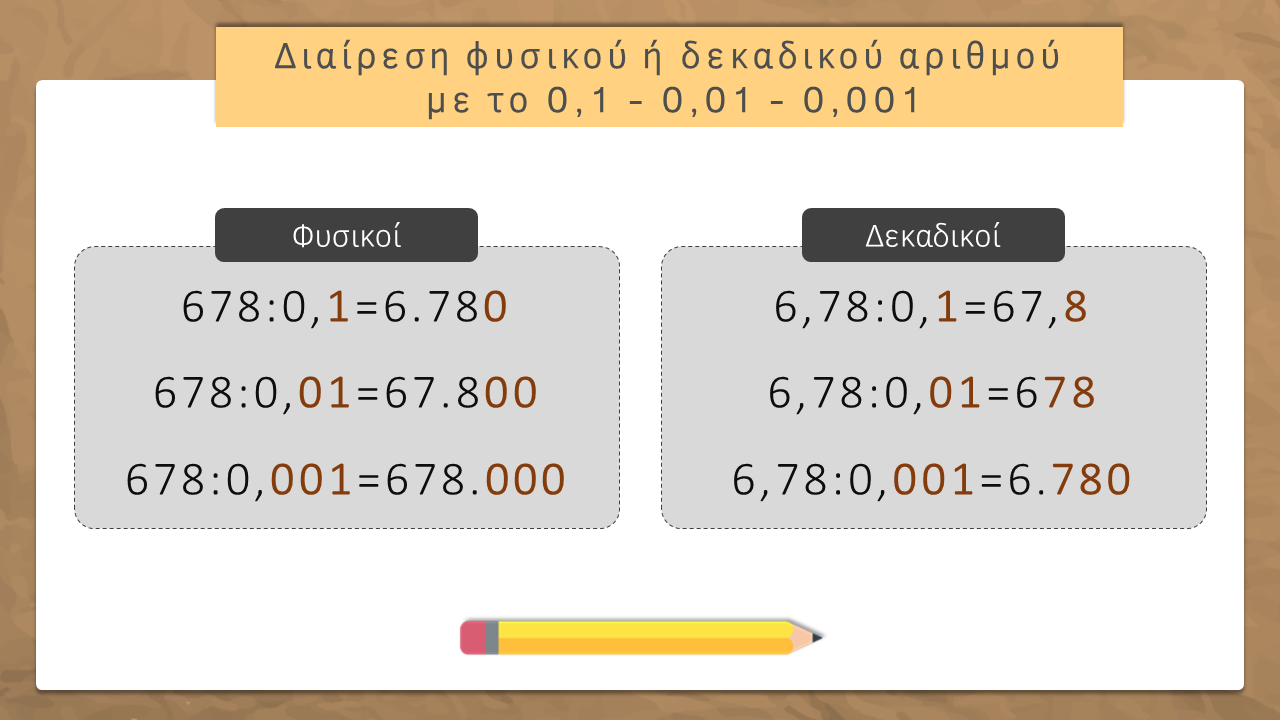
- Όταν διαιρώ έναν αριθμό με 0,1 , 0,01 κτλ ο αριθμός μεγαλώνει, 10, 100, 1.000 φορές.
- Για να διαιρέσω ένα φυσικό αριθμό με το 0,1, το 0,01, το 0,001…, προσθέτω στον αριθμό ένα, δύο ή τρία… μηδενικά αντίστοιχα.
- Για να διαιρέσω ένα δεκαδικό αριθμό με το 0,1, το 0,01, το 0,001…, μεταφέρω την υποδιαστολή του αριθμού δεξιά μία, δύο ή τρεις… θέσεις αντίστοιχα. Αν τελειώσουν τα ψηφία του αριθμού, βάζω μηδενικά.
π
Ο Πυθαγόρας και ο Πυθαγόρειος πίνακας
|
Στην αρχαία Ελλάδα ζούσε ο Πυθαγόρας, μεγάλος φιλόσοφος και μαθηματικός. Γεννήθηκε σε χρονολογία που δεν μας είναι γνωστή, αλλά που εικάζεται πως είναι το 570 π.Χ. και ως επικρατέστερος τόπος γεννήσεως φέρεται η νήσος Σάμος. Είχε εφεύρει έναν «πίνακα», όπως τον έλεγε, που διευκόλυνε τους πολλαπλασιασμούς, οι οποίοι έως τότε γίνονταν με το μυαλό ή απλούστερα με πετραδάκια.
Μας φαίνεται τόσο απλό πράγμα! Ωστόσο, ο Πυθαγόρας αφιέρωσε είκοσι ολόκληρα χρόνια της ζωής του, ώσπου να επινοήσει αυτόν τον πίνακα, ο οποίος έκανε αθάνατο το όνομά του στους κατοπινούς αιώνες. |

ΠΡΟΣΕΧΩ
 Ο πολλαπλασιασμός κάθε αριθμού με το μηδέν δίνει πάντα μηδέν .
Ο πολλαπλασιασμός κάθε αριθμού με το μηδέν δίνει πάντα μηδέν .
0 χ 7 = 0 3,45 χ 0 = 0
 Ο πολλαπλασιασμός κάθε αριθμού με το ένα έχει ως γινόμενο τον ίδιο τον αριθμό .
Ο πολλαπλασιασμός κάθε αριθμού με το ένα έχει ως γινόμενο τον ίδιο τον αριθμό .
7 χ 1= 7 1 χ 2,3 = 2,3
 Στον πολλαπλασιασμό δεκαδικών αριθμών, το πλήθος των δεκαδικών ψηφίων του γινομένου είναι ίδιο με το άθροισμα των δεκαδικών ψηφίων των παραγόντων του.
Στον πολλαπλασιασμό δεκαδικών αριθμών, το πλήθος των δεκαδικών ψηφίων του γινομένου είναι ίδιο με το άθροισμα των δεκαδικών ψηφίων των παραγόντων του.
2, 345 χ 3, 27 = 7, 66815
Πρόσθεση και αφαίρεση φυσικών και δεκαδικών αριθμών
και αφαίρεση φυσικών και δεκαδικών αριθμών

- Στην κάθετη πρόσθεση και την αφαίρεση δεκαδικών αριθμών, οι υποδιαστολές μπαίνουν η μία κάτω από την άλλη. Έτσι τα δέκατα είναι κάτω από τα δέκατα, τα εκατοστά κάτω από τα εκατοστά κτλ.
- Στην κάθετη πρόσθεση ή αφαίρεση δεκαδικών αριθμών, αν οι δεκαδικοί δεν έχουν το ίδιο πλήθος δεκαδικών ψηφίων, για να μη μπερδεύομαι, προσθέτω μηδενικά στο δεκαδικό τους μέρος, έτσι ώστε όλοι να έχουν το ίδιο πλήθος δεκαδικών ψηφίων.






 ΣΥΓΚΡΙΣΗ ΦΥΣΙΚΩΝ Η ΔΕΚΑΔΙΚΩΝ ΑΡΙΘΜΩΝ
ΣΥΓΚΡΙΣΗ ΦΥΣΙΚΩΝ Η ΔΕΚΑΔΙΚΩΝ ΑΡΙΘΜΩΝ



ΜΕΤΑΤΡΟΠΗ ΔΕΚΑΔΙΚΩΝ ΑΡΙΘΜΩΝ ΣΕ ΔΕΚΑΔΙΚΑ ΚΛΑΣΜΑΤΑ
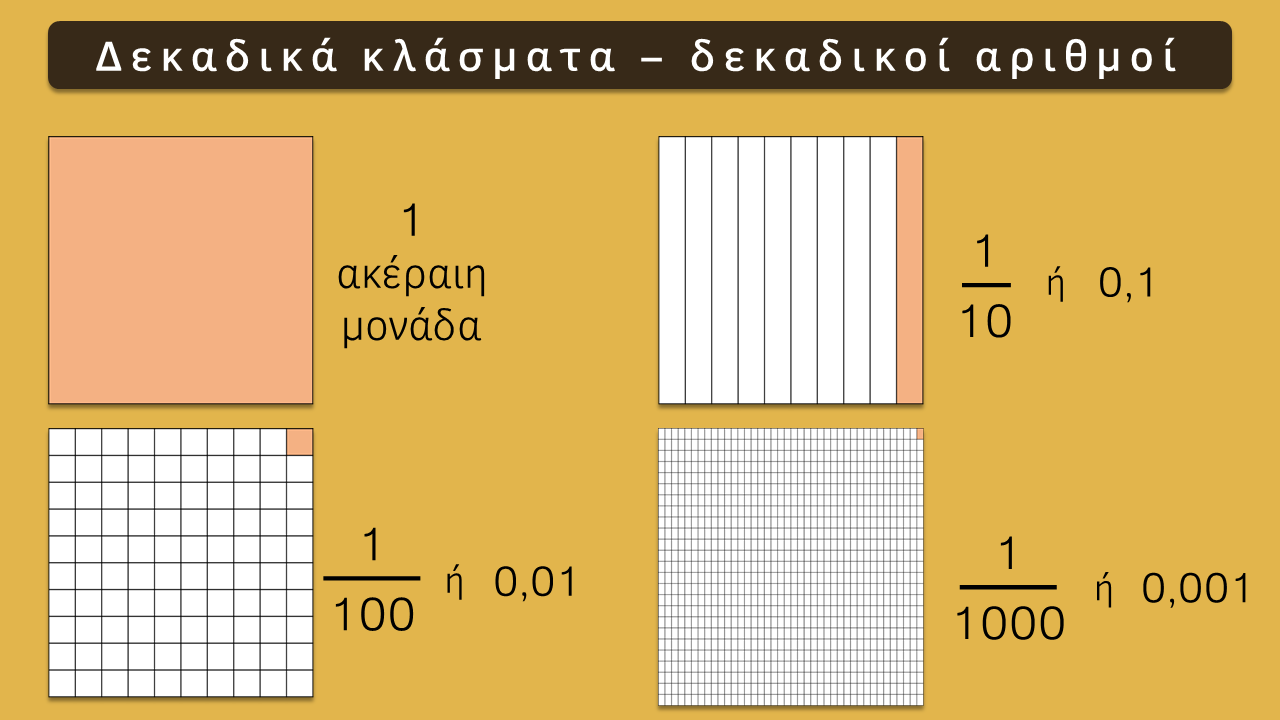
Για να μετατρέψουμε ένα δεκαδικό αριθμό σε δεκαδικό κλάσμα:
- Στη θέση του αριθμητή γράφουμε ολόκληρο τον αριθμό, χωρίς την υποδιαστολή, .
- Στη θέση του παρονομαστή γράφουμε τον αριθμό 1, με τόσα μηδενικά όσα και τα δεκαδικά ψηφία του αριθμού.
Για να μετατρέψουμε ένα δεκαδικό κλάσμα σε δεκαδικό αριθμό:
- Γράφουμε μόνο τον αριθμητή του
- και χωρίζουμε με υποδιαστολή , ξεκινώντας από δεξιά , τόσα δεκαδικά ψηφία, όσα μηδενικά είχε ο παρονομαστής
ΔΕΚΑΔΙΚΟΙ ΑΡΙΘΜΟΙ
Οι δεκαδικοί αριθμοί χρησιμοποιούνται όταν θέλω να εκφράσω με ακρίβεια ένα μέγεθος που δεν μπορεί να εκφραστεί με τη βοήθεια φυσικών αριθμών, όπως οι τιμές διάφορων προϊόντων.
|
Οι αριθμοί αυτοί περιέχουν το ακέραιο μέρος ενός αριθμού και το δεκαδικό μέρος του. Ο χωρισμός ακέραιου και δεκαδικού μέρους γίνεται με την υποδιαστολή (κόμμα).
π.χ. 1 λίτρο βενζίνης κοστίζει 1,568 ευρώ
|
Δέκα μονάδες μιας τάξης είναι μία μονάδα της αμέσως μεγαλύτερης τάξης.
δηλ. 10 εκατοστά = 1 δέκατο , 10 χιλιοστά = 1 εκατοστό
- Τα μηδενικά στο τέλος των δεκαδικών αριθμών δεν έχουν καμία αξία.
8,2 = 8,20 = 8,200
2. Κάθε φυσικός αριθμός μπορεί να γίνει δεκαδικός με την προσθήκη της υποδιαστολής και μηδενικών μετά από αυτή.
23,00 = 23 38 = 38,0 = 38,00
3. Για να ονομάσω ένα δεκαδικό αριθμό, ενεργώ ως εξής:
Χωρίζω το ακέραιο μέρος από δεξιά ανά τρία ψηφία.
Στη συνέχεια, διαβάζω το ακέραιο μέρος όπως ακριβώς και στους φυσικούς, προσθέτω το «και» ή το «κόμμα» και ανάλογα με τη θέση και την αξία του τελευταίου δεκαδικού ψηφίου προσθέτω το ανάλογο συνθετικό (δέκατα, εκατοστά, χιλιοστά).
Παράδειγμα
Τον αριθμό 1340,287 τον γράφω πρώτα ως 1.340,287, οπότε διαβάζω χίλια τριακόσια σαράντα και (ή κόμμα) διακόσια ογδόντα εφτά
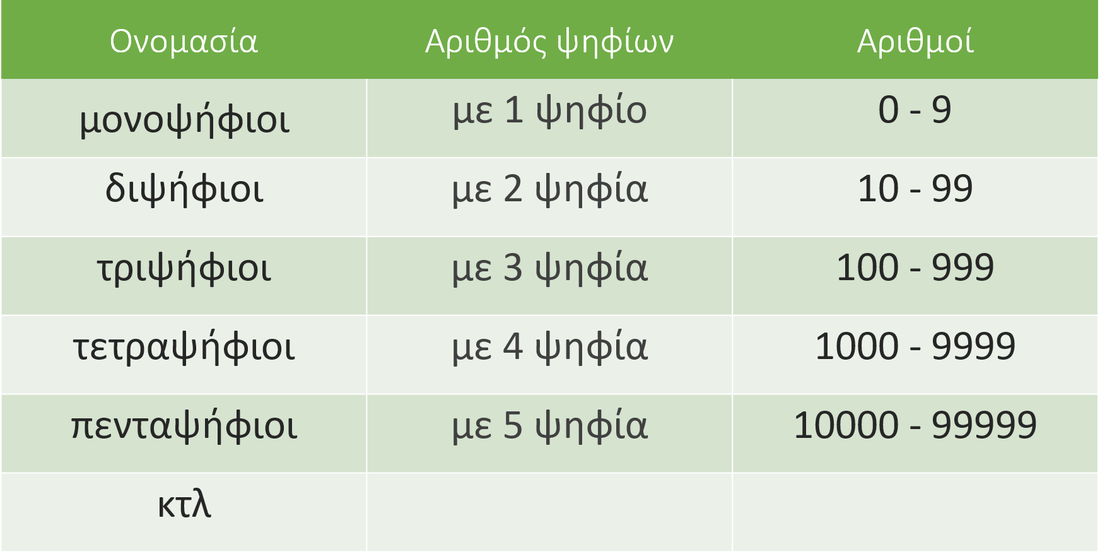
ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ