What are patterns?
Patterns are everywhere. By identifying patterns, we can create rules and solve more-general problems.
Children notice patterns in how teachers react to their behaviour. Weather patterns feed into our forecasts. In maths, pupils can measure the area of a rectangle drawn on graph paper, by counting the number of unit squares within it, but this could be difficult or longwinded for rectangles which are really small or large. A more elegant solution is to multiply the length of the rectangle by the width – and it works well for all rectangles. Once pupils can remember this formula, it’s so much faster than counting squares.
In computing, the method of looking for a general approach to a class of problems is called generalisation.
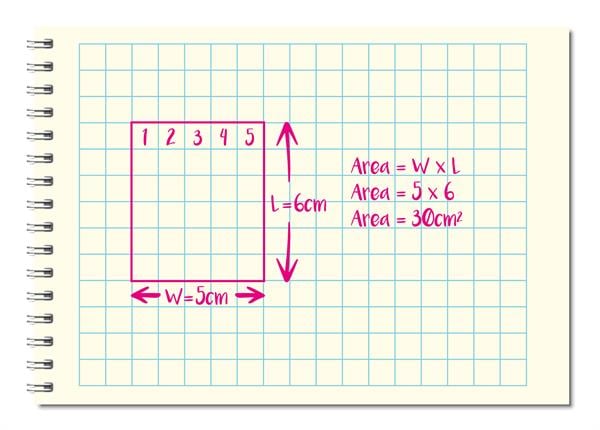
Pupils learn mathematical formulae: these are generalisations.
Why are patterns important?
Computer scientists strive to solve problems quickly and efficiently, and they seek methods applicable elsewhere. If they see a pattern across an algorithm, they’ll look to create a single module of repeatable code, sometimes called a function or procedure – many programming languages have shared libraries of common functions. The recognition of patterns in input data plays an essential role in machine learning. This is an important application of computer science which plays a part in systems for, amongst many other things, algorithmic stock-market trading and the recognition of faces and vehicle number plates.
What do patterns look like in curriculum?
From an early age, children become familiar with repeated phrases in nursery rhymes. Later, they notice repeated structures in stories. We ask pupils to look for and learn from patterns to help them better understand the world. They might recognise common rules (and exceptions) for spellings, and repeating lines in many musical forms. In maths, pupils typically undertake investigations in which they spot patterns and deduce generalised results.

Can pupils spot the pattern to reveal the number-sequence rule?


