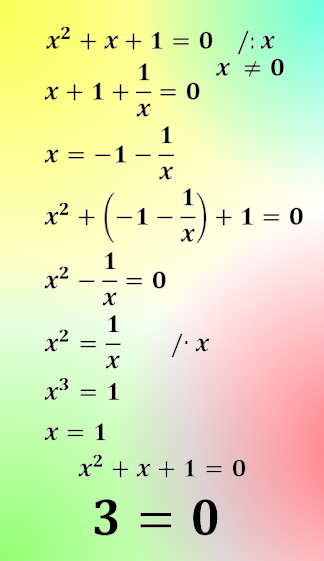Αρχεία για 'Ενδιαφέροντα προβλήματα'
Πού είναι το λάθος?
Συγγραφέας: damianosk2001 στις 5 Αυγούστου 2024
Κατηγορία Ενδιαφέροντα προβλήματα | Δεν επιτρέπεται σχολιασμός στο Πού είναι το λάθος?
Το “θεώρημα” των δύο χρωμάτων
Συγγραφέας: damianosk2001 στις 5 Οκτωβρίου 2022
Αν όλες οι χώρες του κόσμου είχαν κυκλικό σχήμα τότε θα αρκούσαν ΜΟΝΟ δύο χρώματα για να χρωματίσουμε έναν χάρτη ώστε να ΜΗΝ συνορεύουν χώρες με το ίδιο χρώμα!!!!
Απόδειξη: Αν χρωματίσουμε κάθε σημείο που ανήκει σε μονό αριθμό κύκλων άσπρο και κάθε σημείο που εμπεριέχεται σε ζυγό αριθμό κύκλων μαύρο τότε ο χάρτης μας θα έχει συμπληρωθεί!!!
Κατηγορία Ενδιαφέροντα προβλήματα | Δεν επιτρέπεται σχολιασμός στο Το “θεώρημα” των δύο χρωμάτων
Εικασίες πρώτων αριθμών
Συγγραφέας: damianosk2001 στις 5 Οκτωβρίου 2022
Κατηγορία Ενδιαφέροντα προβλήματα | Δεν επιτρέπεται σχολιασμός στο Εικασίες πρώτων αριθμών
Το πρόβλημα της τετράγωνης κρεμάστρας
Συγγραφέας: damianosk2001 στις 21 Ιανουαρίου 2022
Κατηγορία Ενδιαφέροντα προβλήματα | Δεν επιτρέπεται σχολιασμός στο Το πρόβλημα της τετράγωνης κρεμάστρας
Προβληματάκι δημοτικού!
Συγγραφέας: damianosk2001 στις 17 Αυγούστου 2021
Κατηγορία Ενδιαφέροντα προβλήματα | Δεν επιτρέπεται σχολιασμός στο Προβληματάκι δημοτικού!
Πρόβλημα με κύκλους
Συγγραφέας: damianosk2001 στις 16 Ιουνίου 2020
Στο παρακάτω σχήμα ο μεγάλος κύκλος έχει ακτίνα 3μ και ο μικρός 1μ. Αν ο μικρός κύκλος(Β,d) αρχίσει να περιστρέφεται γύρω από τον μεγάλο(A,c) πόσες περιστροφές θα κάνει γύρω από τον εαυτό του μέχρι να φτάσει στην αρχική θέση δλδ σε αυτή που βρίσκεται τώρα; (ΥΓ: Η σωστή απάντηση ΔΕΝ είναι 3 περιστροφές!!!)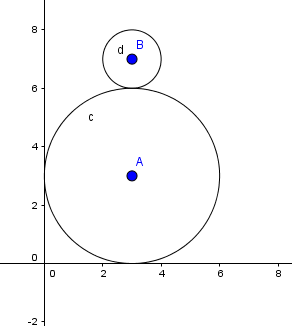
Κατηγορία Ενδιαφέροντα προβλήματα | Δεν επιτρέπεται σχολιασμός στο Πρόβλημα με κύκλους
Τετραγωνική ρίζα του 2
Συγγραφέας: damianosk2001 στις 23 Απριλίου 2020
 Μια καλή απόδειξη για το παραπάνω βρίσκεται στο παρακάτω λινκ: https://www.quora.com/What-is-the-result-of-2-sqrt2-cdot-cdot-cdot-sqrt2
Μια καλή απόδειξη για το παραπάνω βρίσκεται στο παρακάτω λινκ: https://www.quora.com/What-is-the-result-of-2-sqrt2-cdot-cdot-cdot-sqrt2
Κατηγορία Ενδιαφέροντα προβλήματα | Δεν επιτρέπεται σχολιασμός στο Τετραγωνική ρίζα του 2
Τα τέσσερα τεσσάρια!
Συγγραφέας: damianosk2001 στις 10 Φεβρουαρίου 2017
Πώς μπορούμε με 4 4άρια και χρησιμοποιώντας όσες από τις μαθηματικές πράξεις θέλουμε(πρόσθεση, αφαίρεση, πολλαπλασιασμό, διαίρεση, παραγοντικό, λογάριθμο, δυνάμεις, τριγωνομετρία κτλ) να δημιουργήσουμε ΟΛΟΥΣ τους ακεραίους από το 1 ως το άπειρο;
Κατηγορία Ενδιαφέροντα προβλήματα | Δεν επιτρέπεται σχολιασμός στο Τα τέσσερα τεσσάρια!
Γενέθλια
Συγγραφέας: damianosk2001 στις 16 Απριλίου 2015
Κατηγορία Ενδιαφέροντα προβλήματα | Δεν επιτρέπεται σχολιασμός στο Γενέθλια
Ποια γυναικα να παντρευτω;;;
Συγγραφέας: damianosk2001 στις 14 Φεβρουαρίου 2015
ΤΟ ΠΡΟΒΛΗΜΑ ΤΟΥ …ΓΑΜΟΥ ΑΠΟ ΜΑΘΗΜΑΤΙΚΗ ΣΚΟΠΙΑ.
Πολλές φορές στη ζωή μας έχουμε αναρωτηθεί , και έχουμε δεχθεί ερωτήσεις από μαθητές μας, για τη χρησιμότητα των μαθηματικών σε πρακτικά καθημερινά προβλήματα.
Ας υποθέσουμε ότι αποφασίζουμε να βάλουμε βενζίνη στη διάρκεια του ταξιδιού μας και σκεφτόμαστε στρατηγικές για το πώς θα αυξήσουμε τις πιθανότητες να επιλέξουμε το φθηνότερο βενζινάδικο στη διαδρομή μας. Ή ας πούμε ότι χρειάζεται να προσλάβουμε μια γραμματέα και έχουμε τη δυνατότητα να επιλέξουμε ανάμεσα από 20 υποψήφιες. Άλλο παράδειγμα είναι τα τηλεπαιχνίδια τύπου “talent show” στα οποία η επιτροπή καλείται να αποφασίσει για το αν κάποιος υποψήφιος θα συνεχίσει στην επόμενη φάση του παιχνιδιού ή όχι αμέσως μετά την επίδειξη του. Εννοείται πάντα πως θα πρέπει να επιλέξει τους καλύτερους από τους συμμετέχοντες. Τέλος η τόσο σημαντική απόφαση για το ποια θα είναι η μέλλουσα σύζυγος μας δεν μπορεί να λαμβάνεται στην τύχη!!! Τι κοινό έχουν όλα τα παραπάνω καθημερινά προβλήματα; Εκτός του ότι είναι ενδιαφέροντα όλα ανήκουν σε μια ευρύτερη κατηγόρια βελτιστοποίησης του σχετικά καινούργιου κλάδου των μαθηματικών που ονομάζεται θεωρία αποφάσεων και λύνονται με παρόμοιο τρόπο!!!
Ας ξεκινήσουμε κάνοντας κάποιες (λογικές) υποθέσεις για το πρόβλημα του γάμου:
- Οι υποψήφιες μπορούν να αξιολογηθούν από εμάς με έναν αριθμό που περιλαμβάνει την συνολική τους εικόνα. Δυο υποψήφιες ΔΕΝ μπορεί να έχουν ακριβώς τον ίδιο βαθμό.
- Γνωρίζουμε τις υποψήφιες με τυχαία σειρά και μια-μια. Εννοείται ότι απαγορεύεται να έχουμε παράλληλη σχέση!!
- Μπορούμε να προσδιορίσουμε μόνο τη σχετική βαθμολογία κάθε υποψήφιας όπως την γνωρίζουμε. Δεν μπορούμε να γνωρίζουμε την απόλυτη βαθμολογία όλων.
- Ο σκοπός μας είναι να επιλέξουμε την καλύτερη από όλες όσες θα γνωρίσουμε. Οποιαδήποτε άλλη επιλογή θεωρείται αποτυχία.
- Από τη στιγμή που χωρίζουμε με κάποια δεν μπορούμε να επιστρέψουμε και πάλι σε αυτήν.
- Ο αριθμός n των υποψήφιων νυφών που θα γνωρίσουμε μας είναι γνωστός εξ αρχής.
Στην πραγματική ζωή κάποιες από τις υποθέσεις μπορεί να μην ισχύουν επακριβώς. Για παράδειγμα η τελευταία υπόθεση στο πρόβλημα του γάμου δεν ισχύει αλλά μπορούμε προσεγγιστικά να την υπολογίσουμε. Για παράδειγμα αν κάποιος αρχίσει να κάνει σοβαρές σχέσεις από τα 20 του και αναμένει να παντρευτεί μέχρι τα 40 του υποθέτουμε ότι θα γνωρίσει περί τις 27 κοπέλες(μια κάθε 9 μήνες)!!!
Τα (μαθηματικά) ερωτήματα που εύλογα τιθονται είναι:
Ποια στρατηγική πρέπει να ακολουθήσουμε ώστε να μεγιστοποιήσουμε τις πιθανότητες να επιλέξουμε την καλύτερη για σύζυγο;; Τι συμβαίνει όταν το n αυξάνεται; υπάρχει βάσιμη ελπίδα να επιλέξουμε την καλύτερη όταν το n γίνει πολύ μεγάλο;
Στρατηγικές:
Έχουν δημιουργηθεί σε πολλά λογισμικά (όπως στο mathematical) παιχνίδια προσομοίωσης στα οποία μπορεί κάποιος να δοκιμάσει στην πράξη τις στρατηγικές.
Έχοντας παίξει αρκετές φορές κάποιο από αυτά τα παιχνίδια θα διαπιστώσουμε ότι η μόνη αξιόλογη στρατηγική είναι να αφήσουμε τις πρώτες k-1 υποψήφιες να περάσουν (δημιουργώντας ουσιαστικά ένα μέτρο σύγκρισης )και αν η k ή κάποια επόμενη της είναι καλύτερη από ΟΛΕΣ τις προηγούμενες την επιλέγουμε αμέσως για σύντροφο μας. Αν καμία δεν είναι καλύτερη από όλες τις προηγούμενες είμαστε υποχρεωμένοι να επιλέξουμε την τελευταία.
Η παράμετρος k κυμαίνεται μεταξύ του 1 και του n. Αν k=1 τότε επιλέγουμε την πρώτη που θα γνωρίσουμε για γυναίκα μας. Για οποιαδήποτε άλλη τιμή του k η επιλεγμένη για σύζυγος είναι τυχαία τοποθετημένη στο σύνολο {k, k+1, …..n}. Στα επόμενα θα αναφερόμαστε σε αυτήν την στρατηγική ονομάζοντας την ως στρατηγική k.
Επομένως χρειάζεται να υπολογίσουμε τις πιθανότητες pn(k) εφαρμόζοντας τη στρατηγική k με n υποψηφιες.Προσπαθουμε να αυξήσουμε την παραπάνω πιθανότητα επιτυχίας(η k υποψήφια να είναι καλύτερη και των n) χρησιμοποιώντας την καλύτερη στρατηγική και μετά παίρνουμε το όριο όσο αυξάνεται το n για να δούμε την ασυμπτωτικη συμπεριφορά.
Κάνοντας κάποιες δόκιμες υπολογίζουμε εύκολα τις πιθανότητες:
Αν έχουμε 3 μόνο υποψήφιες το καλύτερο είναι να ακολουθήσουμε την 2-στρατηγικη στην οποία έχουμε πιθανότητες 50% να επιλέξουμε την καλύτερη και από τις τρεις. Υπενθυμίζουμε ότι 2-στρατηγικη σημαίνει ότι απορρίπτουμε εξ αρχής την πρώτη υποψήφια και αν η δεύτερη είναι καλύτερη από την πρώτη την παντρευόμαστε. Αν όχι τότε προχωράμε στο να γνωρίσουμε και την 3η και υποχρεωτικά παντρευόμαστε την 3η.
| k | 1 | 2 | 3 |
| pn(k) | 2/6 | 3/6 | 2/6 |
ακολουθώντας παρόμοιο σκεπτικό αν οι υποψήφιες είναι 4 παίρνουμε τον παρακάτω πίνακα:
| k | 1 | 2 | 3 | 4 |
| pn(k) | 6/24 | 11/24 | 10/24 | 6/24 |
Προφανώς και εδώ θα πρέπει να ακολουθήσουμε την 2-στρατηγικη.
Αν οι υποψήφιες είναι 5 έχουμε:
| k | 1 | 2 | 3 | 4 | 5 |
| pn(k) | 24/120 | 50/120 | 52/120 | 42/120 | 24/120 |
Εδώ προτιμότερη είναι η 3-στρατηγικη.
Προφανώς δεν μπορούμε να συνεχίσουμε έτσι. Θα πρέπει να βρούμε έναν γενικό τρόπο υπολογισμού της pn(k) για κάθε n.
Αν n είναι ο αριθμός των υποψήφιων θα συμβολίσουμε με Xn τον αριθμό δηλ. την σειρά με την οποία θα γνωρίσουμε την καλύτερη υποψήφια, και με Sn,k το γεγονός της επιτυχίας της στρατηγικής k.
Το Xn είναι ομοιόμορφα κατανεμημένο στο σύνολο {1,2,…..n} αφού γνωρίζουμε τις υποψήφιες με τυχαία σειρά.
Η δεσμευμένη πιθανότητα P(Sn,k/Xn=j) να επιτύχει η k-στρατηγική και ενώ η καλύτερη όλων είναι στην j σειρά, j{1,2,3…n}.
P(Sn,k/Xn=j)={0, j{1,2,…k-1} & j {k,k+1,…n}}
Το πρώτο σκέλος της ισότητας είναι προφανές αφού αν η καλύτερη υποψήφια είναι στις k-1 πρώτες η k-στρατηγική είναι καταδικασμένη να αποτύχει. Αν η καλύτερη υποψήφια είναι στις υπόλοιπες η k-στρατηγική την εντοπίζει με βεβαιότητα αν και μόνο αν καμία από τις {k, k+1, …j-1} δεν είναι καλύτερη από τις k-1 πρώτες οι οποίες αυτόματα απορρίπτονται. Η αλλιώς αν και μόνο αν ανάμεσα στις k-1 πρώτες υπάρχει κάποια η οποία είναι καλύτερη από τις j-1 πρώτες.
Παίρνοντας τώρα τα αθροίσματα για κάθε δυνατή τιμή του j έχουμε:
Η παραπάνω πιθανότητα προκύπτει αν λάβουμε υπόψη ότι αν η καλύτερη όλων είναι η j υποψήφια τότε η στρατηγική μας την εντοπίζει αν και μόνο αν η καλύτερη ανάμεσα στις πρώτες j-1 (δηλ η δεύτερη καλύτερη όλων) βρίσκεται στις πρώτες k-1 οι οποίες έχουν απορριφθεί.
Αφήνοντας το n να τείνει στο άπειρο και θέτοντας x=lim k/n, χρησιμοποιώντας t=j/n και dt=1/n το παραπάνω άθροισμα Riemann μπορεί να προσεγγιστεί από το ολοκλήρωμα:
Παραγωγιζοντας ως προς χ την παραπάνω συνάρτηση παίρνουμε
P´(x)=-ln(x)-1
Η πρώτη παράγωγος μηδενίζεται όταν το x=e-1.
Σύμφωνα με όσα γνωρίζουμε από την Γ λυκείου η παραπάνω συνάρτηση έχει ολικό μέγιστο όταν το x=e-1 (γιατί πριν το το x=e-1 είναι γν. αύξουσα και μετά είναι γν.φθινουσα)και μάλιστα το μέγιστο αυτό είναι ίσο με το e-1.
Με άλλα λόγια για να μεγιστοποιήσουμε τις πιθανότητες επιλογής της καλύτερης συζύγου θα πρέπει να προσπεράσουμε το 1/e των υποψηφίων που υπολογίζουμε ότι θα γνωρίσουμε (όσο ερωτευμένοι και αν είμαστε με κάποια από αυτές!!) και μετά να παντρευτούμε την πρώτη που θα είναι καλύτερη από όσες έχουμε γνωρίσει μέχρι τότε!! Έτσι θα έχουμε 1/e πιθανότητες να επιλέξουμε την καλύτερη δυνατή! Σε κάθε άλλη περίπτωση οι πιθανότητες είναι λιγότερες.
Για παράδειγμα αν έχουμε να επιλέξουμε ανάμεσα σε 27 κοπέλες θα πρέπει να απορρίψουμε τις 10 πρώτες και να εφαρμόσουμε την 11-στρατηγικη. Ενεργώντας κατά αυτόν τον τρόπο έχουμε 37,97% πιθανότητες να επιλέξουμε την καλύτερη.
Αν υπολογίζουμε ότι θα γνωρίσουμε 40 κοπέλες θα πρέπει να εφαρμόσουμε την 17-στρατηγικη. Ενεργώντας έτσι θα έχουμε 37,5% πιθανότητες να πετύχουμε την καλύτερη. Γενικά όσο το n αυξάνει τόσο οι πιθανότητες επιτυχίας εφαρμόζοντας την 1/e-στρατηγική προσεγγίζουν στον αριθμό 1/e!!!
Το πρόβλημα αυτό πρωτοεμφανίστηκε το 1949 από τον Merril Flood και εκ τοτε έχει επεκταθεί πάρα πολύ δημιουργώντας γενικεύσεις όπως π.χ. τι γίνεται αν αρκούμαστε να επιλέξουμε την 2η καλύτερη όλων και όχι κατ’ ανάγκη την πρώτη. Η ακόμη αν θέλουμε να σχηματίσουμε μια ομάδα r ατόμων τέτοια ώστε όλα να είναι καλύτερα από τα υπόλοιπα κτλ.
Οι μελέτες έχουν δείξει πάντως ότι οι άνθρωποι γενικά έχουν την τάση να σταματάνε νωρίτερα από όσο πρέπει όχι μόνο στο θέμα επιλογής συντρόφου αλλά και σε όλα τα παρόμοια προβλήματα κάτι που ίσως οφείλεται τόσο στην ανθρώπινη ιδιοσυγκρασία όσο και στο κόστος αναζήτησης.
Τέλος ας μας συγχωρέσουν οι γυναίκες διότι στην προσπάθεια μας να απλουστεύσουμε το πρόβλημα τους έχουμε στερήσει το δικαίωμα επιλογής , τις έχουμε χειριστεί για τις ανάγκες του προβλήματος ως άβουλα όντα και θεωρήσαμε το πρόβλημα μόνο από την αντρική σκοπιά (ότι δηλ. δεν υπάρχει περίπτωση να μας απορρίψει κάποια γυναίκα)
Βιβλιογραφία:
http://en.wikipedia.org/wiki/Secretary_problem
http://utilitymill.com/utility/Secretary_Problem_Optimizer
Κανελόπουλος Δαμιανός
damianosk2001@yahoo.com
MSc Μαθηματικός,
Καθηγητής Δευτεροβάθμιας Εκπαίδευσης Δυτικής Θεσσαλονίκης
Κατηγορία Ενδιαφέροντα προβλήματα | Δεν επιτρέπεται σχολιασμός στο Ποια γυναικα να παντρευτω;;;