Το ΠΡΟΒΛΗΜΑ 2 από τις ιταλικές εισαγωγικές εξετάσεις στα πανεπιστήμια τον Ιούνιο του 2024.
«Στην αρχή και στο τέλος, έχουμε το μυστήριο… Τα μαθηματικά μας φέρνουν πιο κοντά σε αυτό το μυστήριο, ακόμα κι αν δεν το διαπερνά». (Ε. Ντε Τζόρτζι)
Εξετάστε την οικογένεια συναρτήσεων ![]() με
με ![]() και
και ![]() ,
, ![]() .
.
- Επαληθεύστε ότι, όποια και αν είναι η τιμή του
 , η συνάρτηση
, η συνάρτηση  δεν είναι παραγωγίσιμη στο σημείο με τετμημένη
δεν είναι παραγωγίσιμη στο σημείο με τετμημένη  . Προσδιορίστε την τιμή του
. Προσδιορίστε την τιμή του  στην οποία το γράφημα της
στην οποία το γράφημα της  έχει γωνιακό σημείο. Για τις κατάλληλες τιμές των παραμέτρων
έχει γωνιακό σημείο. Για τις κατάλληλες τιμές των παραμέτρων  , το γράφημα
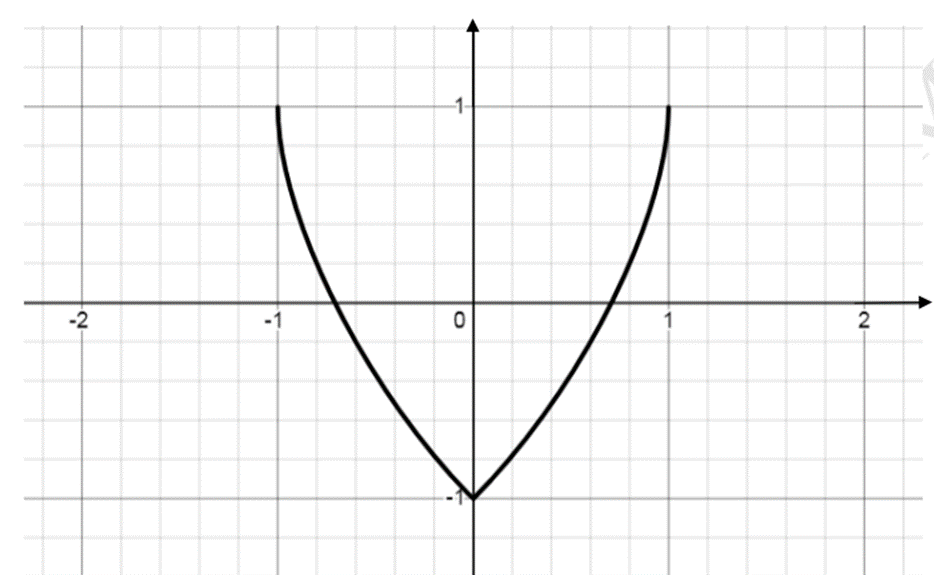
, το γράφημα  , στο σχήμα, αντιπροσωπεύει τη συνάρτηση
, στο σχήμα, αντιπροσωπεύει τη συνάρτηση  Προσδιορίστε τις παραμέτρους
Προσδιορίστε τις παραμέτρους  και
και  , λαμβάνοντας υπόψη ότι η
, λαμβάνοντας υπόψη ότι η  ορίζεται στο
ορίζεται στο ![Rendered by QuickLaTeX.com [-1; 1]](https://blogs.sch.gr/cssamoui/wp-content/ql-cache/quicklatex.com-d526d7c0b95b814abbd32b7df31528f4_l3.png) και ότι το γράφημά είναι συμμετρικό σε σχέση με τον άξονα
και ότι το γράφημά είναι συμμετρικό σε σχέση με τον άξονα  .
.
Από τώρα και στο εξής, ας υποθέσουμε ![]() .
.
- Μελετήστε τη συνάρτηση
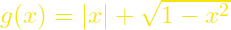 , επαληθεύοντας ότι δεν είναι παραγωγίσιμη στα άκρα του πεδίου ορισμού της και στο σημείο με τετμημένη
, επαληθεύοντας ότι δεν είναι παραγωγίσιμη στα άκρα του πεδίου ορισμού της και στο σημείο με τετμημένη  . Υποδείξτε το γράφημά της με
. Υποδείξτε το γράφημά της με 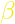 και σχεδιάστε την καμπύλη
και σχεδιάστε την καμπύλη  .
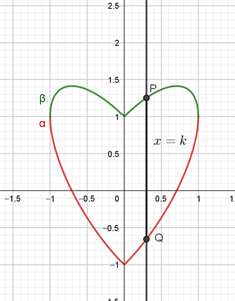
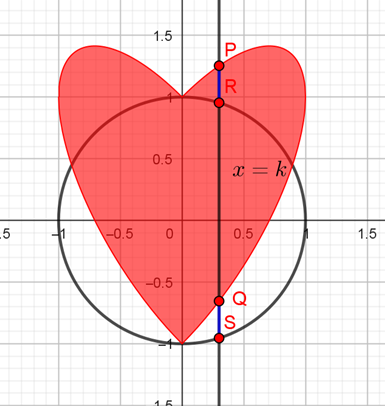
. - Η γραμμή
 , της εξίσωσης
, της εξίσωσης  , με
, με 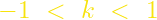 , τέμνει την
, τέμνει την  στα σημεία
στα σημεία  και
και  . Αποδείξτε ότι το μέτρο του τμήματος
. Αποδείξτε ότι το μέτρο του τμήματος  είναι μέγιστο όταν είναι ο άξονας συμμετρίας της
είναι μέγιστο όταν είναι ο άξονας συμμετρίας της  .
. - Βεβαιωθείτε ότι η συνάρτηση
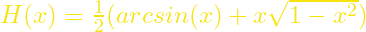 είναι αρχική της συνάρτησης
είναι αρχική της συνάρτησης  . Με τη μέθοδο που θεωρείτε καταλληλότερη, υπολογίστε το εμβαδόν της πεπερασμένης περιοχής του επιπέδου που οριοθετείται από την
. Με τη μέθοδο που θεωρείτε καταλληλότερη, υπολογίστε το εμβαδόν της πεπερασμένης περιοχής του επιπέδου που οριοθετείται από την  .
.
«Οι μορφές που δημιουργούνται από τον μαθηματικό, όπως αυτές που δημιουργούνται από τον ζωγράφο ή τον ποιητή, πρέπει να είναι όμορφες: οι ιδέες, όπως τα χρώματα ή οι λέξεις, πρέπει να συνδέονται αρμονικά. Η ομορφιά είναι η θεμελιώδης προϋπόθεση: δεν υπάρχει μόνιμη θέση στον κόσμο για άσχημα μαθηματικά». (Γ. Χ. Χάρντι)
Λύση
1. Έχουμε ![]() .
.
Επιπλέον
![Rendered by QuickLaTeX.com {\mathop{\mathrm{lim}}_{x\to 0^+} \frac{f_n\left(x\right)-f_n\left(0\right)}{x-0}\ }={\mathop{\mathrm{lim}}_{x\to 0^+} \frac{\sqrt[n]{x^2}-\sqrt{ax^2+bx+1}+1}{x}\ }={\mathop{\mathrm{lim}}_{x\to 0^+} \frac{\sqrt[n]{x^2}}{x}\ }+{\mathop{\mathrm{lim}}_{x\to 0^+} \frac{-\sqrt{ax^2+bx+1}+1}{x}\ }](https://blogs.sch.gr/cssamoui/wp-content/ql-cache/quicklatex.com-6c701aea3a89e707f181f75b8218225e_l3.png)
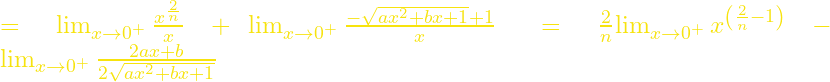 .
.
Για ![]() έχουμε
έχουμε ![]() και
και ![]() , άρα
, άρα ![]() . Όμοια έχω
. Όμοια έχω ![]() με
με ![]() και
και ![]() , άρα
, άρα ![]() .
.
Συνεπώς για ![]() η
η ![]() δεν είναι παραγωγίσιμη στο 0 (έχει κατακόρυφη εφαπτομένη, εκτός ύλης στο ελληνικό σχολείο).
δεν είναι παραγωγίσιμη στο 0 (έχει κατακόρυφη εφαπτομένη, εκτός ύλης στο ελληνικό σχολείο).
Για ![]() έχουμε
έχουμε
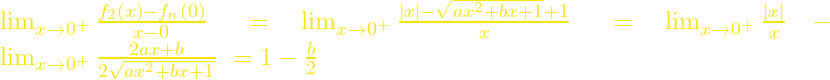 και
και
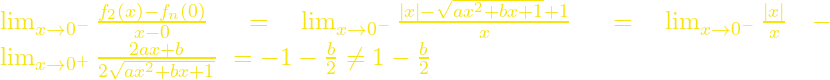 .
.
Άρα και η ![]() δεν είναι παραγωγίσιμη στο 0 (οι πλαϊνές εφαπτόμενες δεν συμπίπτουν, οπότε έχουμε γωνιακό σημείο).
δεν είναι παραγωγίσιμη στο 0 (οι πλαϊνές εφαπτόμενες δεν συμπίπτουν, οπότε έχουμε γωνιακό σημείο).
Αφού το γράφημα της ![]() είναι συμμετρικό ως προς τον άξονα
είναι συμμετρικό ως προς τον άξονα ![]() έχουμε για
έχουμε για ![]() ότι
ότι 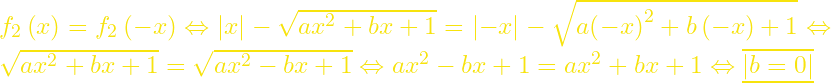 . Από το σχήμα έχουμε
. Από το σχήμα έχουμε ![]() .
.
2. Έχουμε ότι ![]() ,
,
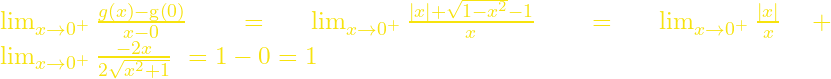 και
και
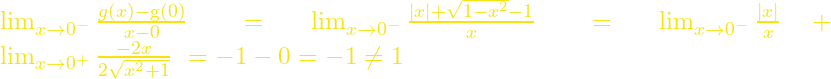
άρα η ![]() δεν είναι παραγωγίσιμη στο
δεν είναι παραγωγίσιμη στο ![]() .
.
Ακόμα έχουμε για το δεξί άκρο του πεδίου ορισμού ότι ![]() και
και 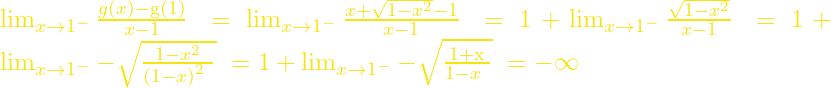 ,
,
άρα η ![]() δεν είναι παραγωγίσιμη στο
δεν είναι παραγωγίσιμη στο ![]() (έχει κατακόρυφη εφαπτομένη). Λόγω συμμετρίας η
(έχει κατακόρυφη εφαπτομένη). Λόγω συμμετρίας η ![]() δεν είναι παραγωγίσιμη και στο
δεν είναι παραγωγίσιμη και στο ![]() .
.
Για το γράφημα της ![]() , έχω για
, έχω για ![]() ότι
ότι ![]() . Έχουμε
. Έχουμε ![]() . Ακόμα έχουμε
. Ακόμα έχουμε 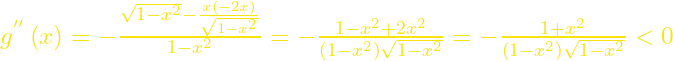 , άρα κοίλη.
, άρα κοίλη.
Προκύπτει ότι ο πίνακας προσήμων είναι ο ακόλουθος
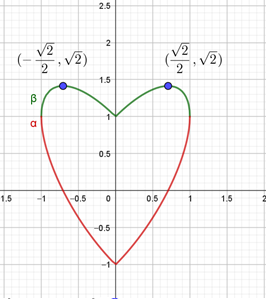
Τελικά έχουμε την καμπύλη ![]() του σχήματος
του σχήματος
3. Έχω ![]() ,
, ![]()
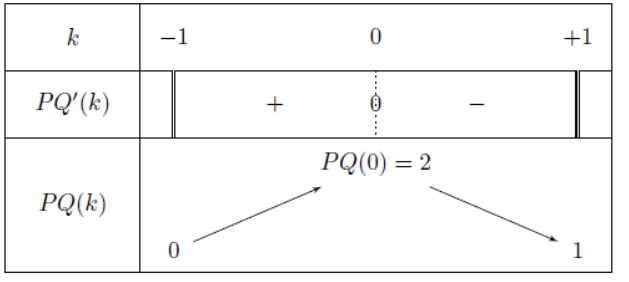
με ![]() και πίνακα προσήμων
και πίνακα προσήμων
Άρα το ![]() μεγιστοποιείται, για
μεγιστοποιείται, για ![]() , δηλαδή όταν το
, δηλαδή όταν το ![]() είναι ο άξονας συμμετρίας της
είναι ο άξονας συμμετρίας της ![]()
4. Έχω ![]()
![]()
Άρα η ![]() είναι αρχική της
είναι αρχική της ![]() . Για το εμβαδόν του χωρίου που εσωκλείεται στην καμπύλη
. Για το εμβαδόν του χωρίου που εσωκλείεται στην καμπύλη ![]() έχω, αφού λάβουμε υπόψην τη συμμετρία της ως προς τον άξονα
έχω, αφού λάβουμε υπόψην τη συμμετρία της ως προς τον άξονα ![]() ότι
ότι ![Rendered by QuickLaTeX.com E_{\gamma}=\int^1_{-1}{\ }(g(x)-f_2(x))dx=2\int^1_0{\ }(g(x)-f_2(x))dx=2\int^1_0{\ }2\sqrt{1-x^2}dx=4\int^1_0{\ }\mathrm{h(x)}dx=4[H(x)]^1_0=2{\left[\mathrm{arcsin}x+x\sqrt{1-x^2}\right]}^1_0=2(\mathrm{arcsin}1-\mathrm{arcsin}0)=\underline{\overline{\left|\pi\right|}}.](https://blogs.sch.gr/cssamoui/wp-content/ql-cache/quicklatex.com-a790f90f96466d66683a35be52a8529a_l3.png)
Μια γεωμετρική ερμηνεία του αποτελέσματος είναι η εξής: Θεωρούμε τον κυκλικό δίσκο με κέντρο την αρχή των αξόνων και ακτίνα ![]() . Καθώς το
. Καθώς το ![]() διατρέχει τις τιμές από το
διατρέχει τις τιμές από το ![]() έως το
έως το ![]() , το τμήμα
, το τμήμα ![]() καλύπτει ακριβώς όλο το χωρίο που βρίσκεται εντός της καμπύλης
καλύπτει ακριβώς όλο το χωρίο που βρίσκεται εντός της καμπύλης ![]() . Όμως, όπως εύκολα συμπεραίνουμε, ισχύει ότι
. Όμως, όπως εύκολα συμπεραίνουμε, ισχύει ότι ![]() και καθώς το
και καθώς το ![]() διατρέχει τις τιμές από το
διατρέχει τις τιμές από το ![]() έως το
έως το ![]() , το τμήμα
, το τμήμα ![]() καλύπτει ακριβώς τον κυκλικό δίσκο εμβαδού
καλύπτει ακριβώς τον κυκλικό δίσκο εμβαδού ![]() . Συνεπώς
. Συνεπώς ![]() .
.


Αφήστε μια απάντηση
Για να σχολιάσετε πρέπει να συνδεθείτε.