S.A.M.

7 Αυγούστου, 2023

Ο καναδικός Fibonacci δεν είναι άρτιας τάξεως.

Κάτω από: Λύσεις —— ΧΡΗΣΤΟΣ ΣΑΜΟΥΗΛΙΔΗΣ @ 3:53 μμ

Το θέμα είναι από καναδικό διαγωνισμό μαθηματικών
Ορίζουμε στους φυσικούς αριθμούς την συνάρτηση f(a,b)=\frac{a}{b}+\frac{b}{a}+\frac{1}{ab} . Για παράδειγμα, f(1,\ 2)=3.
(a) Βρείτε την τιμή του f(2,\ 5).
(b) Βρείτε όλους τους φυσικούς αριθμούς \alpha για τους οποίους ο αριθμός f(a,\ a) είναι φυσικός.
(c) Αν οι \alpha,\ \ \beta καθώς και ο f(a,b) είναι φυσικοί αριθμοί , να δείξετε ότι ο f(a,b) είναι πολλαπλάσιος του 3.
(d) Βρείτε 4 ζεύγη θετικών ακεραίων (a,b) με 2\ <\ a\ <\ b τέτοια, ώστε ο f(a,b) να είναι ακέραιος.

Λύση

α) Απ’ τον ορισμό, έχουμε : f(2,5)=\frac{2}{5}+\frac{5}{2}+\frac{1}{2\cdot5}=\frac{2\cdot2+5\cdot5+1}{2\cdot5}=\frac{4+25+1}{10}=\frac{30}{10}=3

β) Απ’ τον ορισμό, έχουμε : f(a,a)=\frac{a}{a}+\frac{a}{a}+\frac{1}{a^2}=2+\frac{1}{a^2}. Αρκεί το a^2|1, άρα \alpha=\pm1 και αφού α θετικός έχουμε \alpha=1.
γ) Έστω f(a,b)=k\ \in\mathbb{N} . έχουμε τότε \frac{a}{b}+\frac{b}{a}+\frac{1}{ab}=k\ \Longrightarrow\alpha^2+\beta^2+1=kab\ (*).
Αν και το α και το β είναι πολλαπλάσια του 3 τότε από (*) προκύπτει ότι και το 1 είναι πολλαπλάσιο του 3, άτοπο.
Αν \alpha\equiv0\ mod3 και b\equiv1\ ή 2 mod3, τότε από (*) προκύπτει ότι 1^2+0^2+1\equiv0\ mod3, άτοπο.
Αν \alpha\equiv b\equiv1\ ή 2 mod3, τότε από (*) προκύπτει ότι 1^2+1^2+1\equivk\ mod3, άρα ο k είναι πολλαπλάσιος του 3.
Αν \alpha\equiv1\ mod3 και b\equiv\ 2\ mod3, τότε από (*) προκύπτει ότι 1^2+1^2+1\equiv2k\ mod3, άρα ο 2k είναι πολλαπλάσιος του 3, άρα ο k είναι πολλαπλάσιος του 3.
δ) από το α) έχουμε f(5,\ 2)=3.
Ας δούμε αν υπάρχει κι άλλο b με f(5,b)=3. Έχουμε τότε ότι \frac{5}{b}+\frac{b}{5}+\frac{1}{5b}=3 ή 25+b^2+1=15b ή b^2-15b+26=0 ή\ (b-2)(b-13)=0. Άρα b=2 ή b=13
πράγματι f\left(5,13\right)=3.
Η επόμενη σκέψη μας είναι αν υπάρχει κι άλλο b με f\left(13,b\right)=3. Έχουμε τότε ότι \frac{13}{b}+\frac{b}{13}+\frac{1}{13b}=3 ή 169+b^2+1=39b ή b^2-39b+170=0 ή (b-5)(b-34)=0. Άρα b=5 ή b=34. Πράγματι f\left(13,34\right)=3.
Συνεχίζοντας με παρόμοιο τρόπο, μπορούμε επίσης να καταλήξουμε ότι οι f(34,\ 89) και f(89,\ 233) είναι και οι δύο ακέραιοι αριθμοί.
Έτσι, τα ζεύγη (a,\ b)\ =\ (5,\ 13),\ (13,\ 34),\ (34,\ 89),\ (89,\ 233) ικανοποιούν τις απαιτήσεις του προβλήματος.
Πώς όμως προκύπτουν αυτοί οι αριθμοί; Που τους έχουμε ξαναδεί;

Ορίζουμε την ακολουθία Fibonacci F_1,F_2,F_3,F_4,\ldots ως εξής: F_1=F_2=1 and F_n=F_{n-1}+F_{n-2} όπου n\geq3. Έτσι η ακολουθία Fibonacci ξεκινά ως εξής 1,1,2,3,5,8,13,21,34,55,89,\ldots.
Τα ζεύγη \left(a,b\right) που βρήκαμε ως τώρα είναι της μορφής \left(F_{2k-1},F_{2k+1}\right)\mathrm{\ }με k\geq3.
Θα δείξουμε λοιπόν ότι f\left(F_{2k-1},F_{2k+1}\right)=3 για κάθε k\geq3.
Έχουμε f\left(F_{2k-1},F_{2k+1}\right)=3 ή
(F_{2k-1})^2+(F_{2k+1})^2+1=3F_{2k-1}F_{2k+1} ή
(F_{2k-1})^2+(F_{2k}+F_{2k-1})^2+1=3F_{2k-1}(F_{2k}+F_{2k-1}) ή
2(F_{2k-1})^2+2F_{2k}F_{2k-1}+(F_{2k})^2+1=3F_{2k-1}F_{2k}+3{{(F}_{2k-1})}^2 ή
(F_{2k})^2+1=F_{2k-1}F_{2k}+{{(F}_{2k-1})}^2 ή (F_{2k})^2+1=F_{2k-1}F_{2k+1} ή (F_{2k})^2-F_{2k-1}F_{2k+1}=-1 (**) που ισχύει για κάθε k\geq3.
Απόδειξη της (**) με επαγωγή.
Για k=3 έχουμε \bigm(F_{2\cdot3})^2-F_{2\cdot 3-1}F_{2\cdot 3+1}=(F_6)^2-F_5F_7=8^2-5\cdot 13=-1
Δεχόμενοι ότι ισχύει η (F_{2k})^2-F_{2k-1}F_{2k+1}=-1 θα δείξουμε την ισχύ της (**) για k+1
Έχουμε
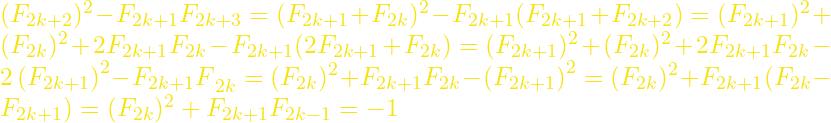(F_{2k+2})^2-F_{2k+1}F_{2k+3}= (F_{2k+1}+F_{2k})^2-F_{2k+1}(F_{2k+1}+F_{2k+2})= (F_{2k+1})^2+(F_{2k})^2+2F_{2k+1}F_{2k}-F_{2k+1}(2F_{2k+1}+F_{2k})= (F_{2k+1})^2+(F_{2k})^2+2F_{2k+1}F_{2k}-{2\left(F_{2k+1}\right)}^2-{F_{2k+1}F}_{2k}= (F_{2k})^2+F_{2k+1}F_{2k}-\left(F_{2k+1}\right)^2= (F_{2k})^2+F_{2k+1}(F_{2k}-F_{2k+1})= (F_{2k})^2+F_{2k+1}F_{2k-1}=-1 και η απόδειξη ολοκληρώθηκε.

2ος τρόπος.
Έχουμε ότι αν \frac{a}{b}+\frac{b}{a}+\frac{1}{ab}=3\ \Longrightarrow\alpha^2+\beta^2+1=3ab (***)
f\left(b,3b-a\right)=\frac{b}{3b-a}+\frac{3b-a}{b}+\frac{1}{b\left(3b-a\right)}=\frac{b^2+(3b-a)^2+1}{b\left(3b-a\right)}=\frac{{10b}^2-6ab+a^2+1}{b\left(3b-a\right)}= \frac{9b^2-3ab-3ab+a^2+b^2+1}{b\left(3b-a\right)}
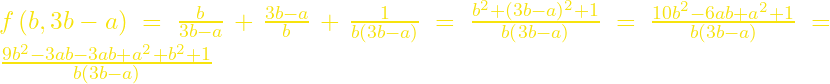
Λόγω της (***) έπεται ότι f(b,3b-a)=\frac{9b^2-3ab}{b(3b-a)}=3
Συνεπώς, αν f\left(a,b\right)=3 , τότε f\left(b,3b-a\right)=3
Η εξίσωση f\left(1,2\right)=3 δίνει f\left(2,\ 3\cdot 2-1\right)=f\left(2,\ 5\right)=3
Η εξίσωση f\left(2,5\right)=3 δίνει f\left(5,\ 3\cdot 5-2\right)=f\left(5,\ 13\right)=3
Η εξίσωση f\left(5,13\right)=3 δίνει f\left(13,\ 3\cdot 13-5\right)=f\left(13,\ 34\right)=3
Η εξίσωση f\left(13,34\right)=3 δίνει f\left(34,\ 3\cdot 34-13\right)=f\left(34,\ 89\right)=3
Η εξίσωση f\left(34,89\right)=3 δίνει f\left(89,\ 3\cdot 89-34\right)=f\left(89,\ 233\right)=3
Κι επομένως τα ζεύγη \left(a,b\right)=\left(5,13\right)\ ,(13,34),\ (34,89),\ (89,233) ικανοποιούν τις απαιτήσεις του προβλήματος.

Αφήστε μια απάντηση

«
»

©2025 S.A.M. Φιλοξενείται από Blogs.sch.gr

Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH