S.A.M.

11 Απριλίου, 2023

Ο Ευκλείδης προτείνει… Άσκηση 393

Κάτω από: Λύσεις —— ΧΡΗΣΤΟΣ ΣΑΜΟΥΗΛΙΔΗΣ @ 10:16 πμ

Το μαθηματικό περιοδικό “Ευκλείδης” προτείνει…

Ευκλείδης B’ 127 (2023) τ.3/57

Άσκηση 393

Δίνεται κύβος ΑΒΓΔΕΖΗΘ με ακμή α = 1, απέναντι έδρες τις ΑΒΓΔ και ΕΖΗΘ και με κατακόρυφες ακμές τις ΑΕ, ΒΖ, ΓΗ και ΔΘ. Στην ακμή ΑΔ θεωρούμε τμήμα \Delta K = \frac{1}{4}, στην ΒΑ τμήμα B\Lambda} = \frac{1}{4}, στη ΖΗ τμήμα ZM = \frac{1}{4} και στην ΗΘ τμήμα \Theta N = \frac{1}{4}.  Να υπολογίσετε το εμβαδόν του τετραπλεύρου ΚΛΜΝ.            Φρουντζής Βασίλης – Αγρίνιο

 

Λύση

393

Από την ισότητα \frac{AK}{A\Delta} = \frac{A\Lambda}{AB} = \frac{3}{4} ,  συμπεραίνουμε ότι ΚΛ//ΒΔ, ομοίως ΜΝ//ΘΖ και από την προφανή παραλληλία των διαγωνίων ΒΔ και ΘΖ προκύπτει ότι ΚΛ//ΜΝ . Από τα ισοσκελή και ορθογώνια τρίγωνα ΑΚΛ, ΗΜΝ, έχουμε K\Lambda = MN( = \sqrt{2}\frac{3}{4}\alpha = \frac{3\sqrt{2}}{4}) οπότε το ΚΛΜΝ είναι παραλληλόγραμμο.

Από το Λ φέρουμε κάθετη ΛΠ στο επίπεδο της άνω βάσης ΕΖΘΗ οπότε από το ορθογώνιο τρίγωνο ΠΜΛ, έχουμε: M\Lambda^{2} = \Pi M^{2} + \Pi\Lambda^{2} = \Pi Z^{2} + ZM^{2} + \alpha^{2} = \left( \frac{1}{4} \right)^{2} + \left( \frac{1}{4} \right)^{2} + 1 = \frac{9}{8}.

Άρα M\Lambda = \sqrt{\frac{9}{8}} = \frac{3\sqrt{2}}{4} = K\Lambda

Επιπλέον, \widehat{\Pi MN} = 180^{ο} -ZM\Pi - HMN = 180^{o} - 45^{o} - 45^{o} = 90^{o} , άρα \Pi M\bot MN

Τέλος  M\Pi\bot \Pi\Lambda, άρα από το θεώρημα των τριών κάθετων προκύπτει ότι MN\bot M\Lambda. Επομένως το ΚΛΜΝ είναι τετράγωνο με εμβαδόν (K\Lambda MN) = M\Lambda^{2} = \frac{9}{8}

 

Β’ τρόπος.

Έστω καρτεσιανό σύστημα συντεταγμένων με το Α(0,0,0) στην αρχή των αξόνων, τα Β, Δ, Ε στους άξονες των x, y, z αντίστοιχα.

Άρα έχουμε \Lambda(0.75, 0, 0), K(0, 0.75, 0) και M(1, 0.25, 1). Οπότε \overrightarrow{K\Lambda} = (0.75, - 0.75, 0) και
\overrightarrow{\Lambda M} = (0.25, 0.25, 1)
(K\Lambda MN) = \overrightarrow{K\Lambda}\ \times \overrightarrow{\Lambda M} = \left| \begin{matrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ 0.75 & - 0.75 & 0 \\ 0.25 & 0.25 & 1 \\ \end{matrix} \right| = \left| - 0.75\overrightarrow{i} - 0.75\overrightarrow{j} + 0.375\overrightarrow{k} \right| = 0.375\left| \overrightarrow{2i} + \overrightarrow{2j} + \overrightarrow{k} \right| = \frac{3}{8}\sqrt{2^{2} + 2^{2} + 1^{2}} = \frac{3}{8} \cdot 3\)=\(\ \frac{9}{8}

 

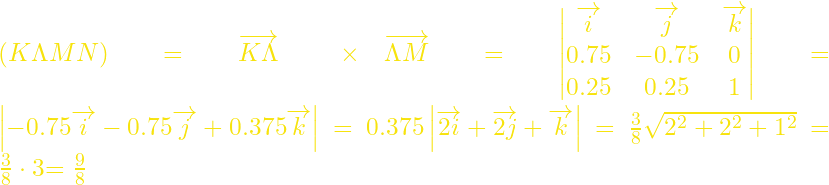
Αφήστε μια απάντηση

«
»

©2025 S.A.M. Φιλοξενείται από Blogs.sch.gr

Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH