S.A.M.

31 Αυγούστου, 2022

Περιτετράγωνο

Κάτω από: β' λυκείου μαθηματικά κατεύθυνσης —— ΧΡΗΣΤΟΣ ΣΑΜΟΥΗΛΙΔΗΣ @ 11:18 πμ

Έστω το τετράπλευρο ABCD με συντεταγμένες A(0,8), B(1,0), C(5,0), D(7,6)

Να περιγράψετε το τετράπλευρο ABCD σε ένα τετράγωνο SPQT και να υπολογίσετε το εμβαδόν του τετραγώνου.

peritetragono

Απάντηση

Για την ευθεία QT έχουμε: y=\lambda x+b_{1}, \lambda>0 \xrightarrow{C(5,0)\in QT} 0=5\lambda+b_{1}
Για την ευθεία PS // QT έχουμε: y=\lambda x+b_{2}, b_{2}>b_{1} \xrightarrow{A(0,8)\in PS} 8=0\lambda+b_{2}
Για την ευθεία PQ \bot QT έχουμε: y=-\frac{1}{\lambda} x+b_{3} \xrightarrow{B(1,0)\in PQ} 0=-\frac{1}{\lambda}+b_{3}
Για την ευθεία ST // PQ έχουμε: y=-\frac{1}{\lambda}x+b_{4}, b_{4}>b_{3} \xrightarrow{D(7,6)\in ST} 6=-\frac{7}{\lambda}+b_{4}
Οι ανισότητες προκύπτουν από το σχήμα.

Για να είναι τετράγωνο το SPQT αρκεί οι αποστάσεις των 2 ζευγών από παράλληλες ευθείες να είναι ίσες.
Οπότε d(\epsilon_{PQ},\epsilon_{ST})=d(\epsilon_{PS},\epsilon_{QT})\Rightarrow \frac{|b_{4}-b_{3}|}{\sqrt{1+\frac{1}{\lambda^2}}}=\frac{|b_{2}-b_{1}|}{\sqrt{1+\lambda^2}}\Rightarrow |\lambda|\frac{b_{4}-b_{3}}{\sqrt{1+\lambda^2}}=\frac{b_{2}-b_{1}}{\sqrt{1+\lambda^2}} \Rightarrow \lambda(6+\frac{7}{\lambda}-\frac{1}{\lambda})=8+5\lambda
και τελικά \lambda=2, b_{1}=-10,b_{2}=8,b_{3}=\frac{1}{2},b_{4}=\frac{19}{2}, δεκτές.

Για το εμβαδόν έχουμε (SPQT)=d^2(\epsilon_{PS},\epsilon_{QT})=\frac{(b_{2}-b_{1})^{2}}{1+\lambda^2}=\frac{18^2}{5}=64,8 \tau.\mu.

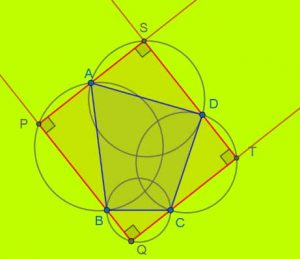
Ενδιαφέρουσα είναι και η γεωμετρική κατασκευή των άπειρων “περιορθογωνίων” ενός τετραπλεύρου.

perior8ogonia

Ανοίξτε τον παρακάτω σύνδεσμο για να διαπιστώσετε πως μπορούμε να κατασκευάσουμε άπειρα περιγεγγραμμένα ορθογώνια ενός κυρτού τετραπλεύρου.

https://www.geogebra.org/m/ayzyaawc

 

 

Αφήστε μια απάντηση

«
»

©2024 S.A.M. Φιλοξενείται από Blogs.sch.gr

Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH