S.A.M.

Ο Ευκλείδης Προτείνει…
ΕΥΚΛΕΙΔΗΣ Β’ 124 (2022) τ.4/1

Άσκηση 392

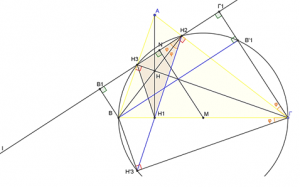
Θεωρούμε τρίγωνο ΑΒΓ και τα ύψη του . Αν οι προβολές των Β και Γ στην ευθεία να αποδείξετε ότι:
α. β.
Σταματιάδης Βαγγέλης – Ν. Ιωνία
Λύση

α Έχω , αφού και είναι ύψη του ΑΒΓ. Άρα το είναι εγγράψιμο σε κύκλο (c) με διάμετρο το ΒΓ. Έστω Μ μέσο του ΒΓ, άρα Μ κέντρο του κύκλου (c), από το οποίο φέρω το (κάθετο) απόστημα στην χορδή στο σημείο Ν. Οπότε, το Ν είναι μέσο του , άρα (1).

Αφού τα είναι κάθετα στην ευθεία άρα , άρα το είναι τραπέζιο και, αφού Μ μέσο του ΒΓ, το ΜΝ είναι διάμεσος του τραπεζίου. Άρα το Ν είναι μέσο του . Συνεπώς, (2). Αφαιρώντας τις (1) και (2) κατά μέλη έχουμε .

β Από το Β φέρω κάθετη στο , όποτε στο ορθογώνιο , έχουμε . Η προέκταση του τέμνει τον κύκλο στο . Στο ορθικό τρίγωνο το Η είναι έκκεντρο, άρα . Τώρα, τα τρίγωνα και είναι ορθογώνια και ίσα (γιατί;). Άρα , άρα ΒΓ μεσοκάθετος του , άρα και τελικά (**)

Οι οξείες γωνίες και έχουν κάθετες πλευρές, άρα ίσες. Οπότε έχουμε διαδοχικά . Άρα από (**) έχουμε