Να αποδειχθεί η ταυτότητα:
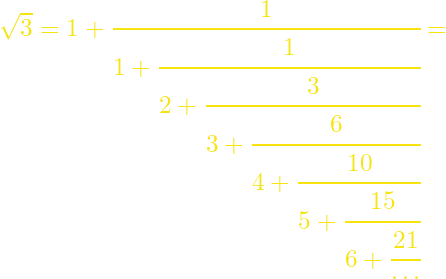
Λύση
Έστω ότι ![]()
θα δείξουμε ότι ![]()
Πράγματι
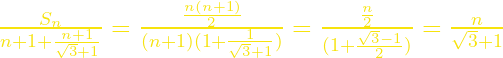
Άρα
![]()
![]()
![]()
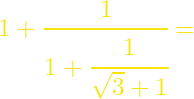 (από *)
(από *)
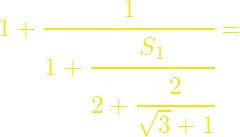 (από *)
(από *)
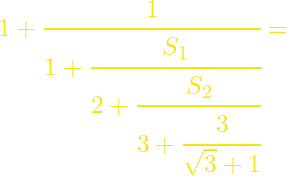 (από *)
(από *)
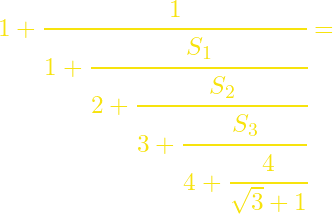
klp
Να αποδειχθεί η ταυτότητα:
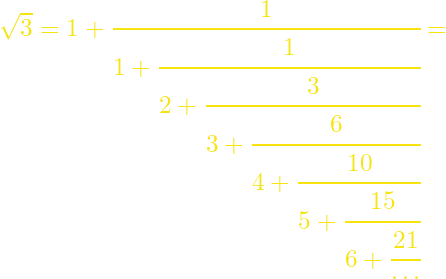
Λύση
Έστω ότι ![]()
θα δείξουμε ότι ![]()
Πράγματι
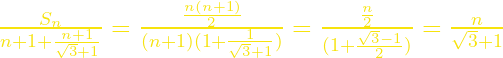
Άρα
![]()
![]()
![]()
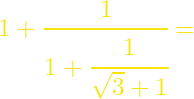 (από *)
(από *)
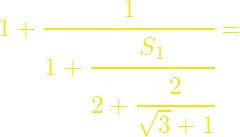 (από *)
(από *)
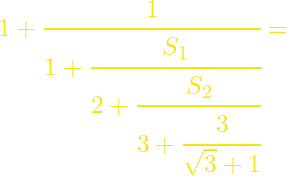 (από *)
(από *)
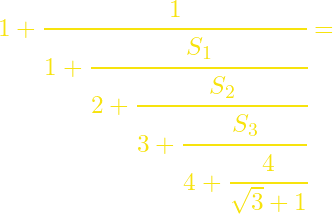
klp
©2025 S.A.M. Φιλοξενείται από Blogs.sch.gr
Αφήστε μια απάντηση
Για να σχολιάσετε πρέπει να συνδεθείτε.