S.A.M.

8 Ιουνίου, 2021

Εμβαδόν περιοχής

Κάτω από: Λύσεις —— ΧΡΗΣΤΟΣ ΣΑΜΟΥΗΛΙΔΗΣ @ 6:11 μμ

Στο παρακάτω σχήμα δίνεται τετράγωνο με πλευρά 10α, δύο ημικύκλια και ένα τεταρτοκύκλιο. Να βρείτε το εμβαδόν της γαλάζιας περιοχής συναρτήσει του α. Δεκτές όλες οι λύσεις!

Έστω σύστημα αξόνων με αρχή τους το Α.Τότε το Σ που είναι το κέντρο του τετραγώνου είναι το σημείο Σ(5,5).

  •  Τότε έχω για το ημικύκλιο ΔΣΑ ότι 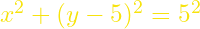x^2+(y-5)^2=5^2 άρα για το τόξο ΔΣ ισχύει
    f_1(x)=5+\sqrt{5^2-x^2}
  •  Το τόξο ΔΤ είναι στο ημικύκλιο με κέντρο το Α και ακτίνα 10 άρα f_2(x)=\sqrt{10^2-x^2}
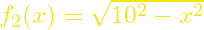
  •  Το ημικύκλιο ΔΣΓ έχει κέντρο το (5,10) άρα 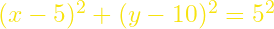(x-5)^2+(y-10)^2=5^2 και η αντίστοιχη συνάρτηση είναι η f_3(x)=10-\sqrt{5^2-(x-5)^2}
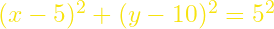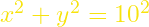  • To Τ είναι το σημείο τομής των (x-5)^2+(y-10)^2=5^2 και x^2+y^2=10^2 με αποδεκτή λύση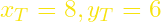 x_T=8,y_T=6

Άρα

E=\int_0^5 (f_2(x)-f_1(x))\,dx+\int_5^8 (f_2(x)-f_3(x))\,dx=

E=\int_0^5 \sqrt{10^2-x^2}-(5+\sqrt{5^2-x^2})\,dx + \int_5^8 (\sqrt{10^2-x^2}-(10-\sqrt{(5^2-(x-5)^2}))\,dx

 

=

 

\int_0^8 \sqrt{10^2-x^2}dx-25-\int_0^5\sqrt{5^2-x^2})\,dx -30-\int_5^8\sqrt{(5^2-(x-5)^2})\,dx

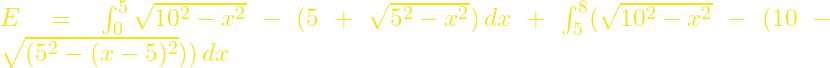
Για το πρώτο ολοκλήρωμα θέτω: x=10\eta\mu\theta οπότε dx=10\sigma\upsilon\nu \vartheta\, d\vartheta με όρια το 0 και το \vartheta_1=\tau o\xi\eta\mu(4/5).

Άρα \int_0^8 \sqrt{10^2-x^2}\,dx=\int_0^{\theta _1} 10\sigma\upsilon\nu\vartheta10\sigma\upsilon\nu\theta\,d\vartheta=
10^2\int_0^{\theta _1} \sigma\upsilon\nu^2\vartheta\,d\vartheta=
10^2\int_0^{\theta _1} \frac{1+\sigma\upsilon\nu2\vartheta}{2}\,d\vartheta=
10^2 ( \frac{\vartheta_1 }{2}+\frac{\eta\mu2\theta_1}{2\cdot2})

Για το δεύτερο ολοκλήρωμα \int_0^5\sqrt{5^2-x^2})\,dx=εμβαδόν τεταρτοκυκλίου με ακτίνα 5 άρα ίσο με \frac{\pi\cdot5^2}{4}

Για το τρίτο ολοκλήρωμα \int_5^8\sqrt{(5^2-(x-5)^2})\,dx =\int_0^3\sqrt{(5^2-z^2})\,dz= 5^2 ( \frac{\vartheta_2 }{2}+\frac{\eta\mu2\theta_2}{2\cdot2}) (όπως πριν εδώ θ2 η γωνία με ημίτονο 3/5)

Τελικά έχουμε

Ε= 50\cdot\tau o\xi\eta\mu\frac{4}{5}+10^2\cdot\frac{2\cdot\frac{4}{5}\cdot\frac{3}{5}}{2\cdot2}-25-\frac{\pi\cdot5^2}{4}-30+\frac{25\tau o\xi\eta\mu\frac{3}{5}}{2}+5^2\cdot\frac{2\cdot\frac{3}{5}\cdot\frac{4}{5}}{2\cdot2}= 50\cdot\tau o\xi\eta\mu\frac{4}{5}+24-25-\frac{\pi\cdot5^2}{4}-30+25\tau o\xi\eta\mu\frac{3}{5}+6 =46.36+8.04-19.63-25=9.77

 

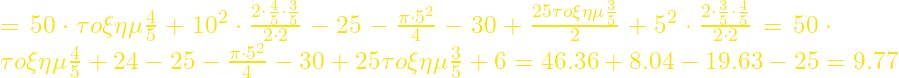
β’ τρόπος (με χρήση πολικών συνεταγμένων)

Έστω σύστημα αξόνων με αρχή τους το Δ και τον θετικό ημιάξονα των y προς τα κάτω!
Τότε έχω r_{\Delta\Sigma A}(\vartheta)=10\eta\mu\theta, \,\vartheta \in [0,\pi/2], r_{\Delta\Sigma \varGamma}(\vartheta)=10\sigma\upsilon\nu\theta , \,\vartheta \in [0,\pi/2], r_{\Delta TB}(\vartheta)=20\eta\mu\theta, \,\vartheta \in [0,\pi/4]

Αν η γωνία \Gamma\Delta\varSigma =\vartheta_1 έχω r_{\Delta\Sigma \varGamma}(\vartheta_1)=r_{\Delta TB}(\vartheta_1)\Leftrightarrow 10\sigma\upsilon\nu\theta_1 = 20\eta\mu\theta_1\Leftrightarrow \epsilon\varphi\theta_1=1/2
άρα \eta\mu\theta_1=1/\sqrt{5}, \sigma\upsilon\nu\theta_1=2/\sqrt{5}, \eta\mu(2\theta_1)=4/5

Γενικά E=\frac{1}{2}\int_{\theta_1}^{\theta_2} r_1^2(\theta) - r_2^2(\theta) \, d\theta

Εδώ έχουμε E=\frac{1}{2}\int_0^{\theta_1}r_{\Delta TB}^2(\theta) - r_{\Delta\Sigma A}^2(\theta) \, d\theta+ \frac{1}{2}\int_{\theta_1}^{\pi/4} r_{\Delta\Sigma \varGamma}^2(\theta) - r_{\Delta\Sigma A}^2(\theta) \, d\theta =

\frac{1}{2}\int_0^{\theta_1}20^2\eta\mu^2(\theta) - 10^2\eta^2\mu(\theta) \, d\theta+ \frac{1}{2}\int_{\theta_1}^{\pi/4} 10^2\sigma\upsilon\nu^2(\theta) - 10^2 \eta\mu^2(\theta) \, d\theta =

150\int_0^{\theta_1}\eta\mu^2(\theta)\, d\theta+50\int_{\theta_1}^{\pi/4} \sigma\upsilon\nu(2\theta) \, d\theta

Έχω \int_0^{\theta} \eta\mu^2(\theta)= \frac{\vartheta}{2}-\frac{\eta\mu(2\theta)}{4} και \int_0^{\theta} \sigma\upsilon\nu(2\theta)= \frac{\eta\mu(2\theta)}{2}

Άρα E=150(\frac{\vartheta_1}{2}-\frac{\eta\mu(2\theta_1)}{4})+50(\frac{\eta\mu(\pi/2)}{2}-\frac{\eta\mu(2\vartheta_1)}{2})=

75\cdot\tau o\xi\eta\mu(1/\sqrt{5})-30+25-25\cdot\frac{4}{5}=9.77

Αφήστε μια απάντηση

«
»

©2025 S.A.M. Φιλοξενείται από Blogs.sch.gr

Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH