σύγχρονος ΓΑΙΟ-ΓΕΩμέτρης

Μια μικρή αναφορά πληροφοριών… και "Ουδείς αγεωμέτρητος εισήτω."

Άρθρα κατηγορίας "Γενικά"

π – Pi = 3,14159…………………….

Μάι 21 24

Αναρτήθηκε από ΝΙΚΟΣ ΠΑΝΟΥΣΟΠΟΥΛΟΣ. Κατηγορία: Γενικά | Χωρίς σχόλια

 

. .. ………….  … …

π / e – ΖΑΡΙ / ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

Ιούν 13 4

Αναρτήθηκε από ΝΙΚΟΣ ΠΑΝΟΥΣΟΠΟΥΛΟΣ. Κατηγορία: Γενικά | Χωρίς σχόλια

ΤΟ ΣΥΝΔΙΚΑΤΟ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ:

 

Οι παρακάτω μετρήσεις έγιναν με το παρακάτω εργαλείο που αναπτύχθηκε για τους μαθητές του 3ου Γυμνασίου Κορίνθου:

http://users.sch.gr/nikpanous/calca/pi_stat2.htm

 

e / Στατιστικά:

Τα στατιστικά στοιχεία του δεκαδικού μέρους του e δίνουν παρόμοιο αποτέλεσμα με το π δηλαδή έχουμε τον defacto κανόνα του 10%.

 

 

 

π – Pi / Στατιστικά:

 

 

Ετικέτες:

Προοίμιο.

Νοέ 09 6

Αναρτήθηκε από ΝΙΚΟΣ ΠΑΝΟΥΣΟΠΟΥΛΟΣ. Κατηγορία: Γενικά | Κλειστά Σχόλια

 Στο επεισόδιο του Σταρ Τρεκ “Λύκος στο κοπάδι“ ο Σποκ ματαιώνει τα σατανικά σχέδια ενός υπολογιστή, ζητώντας του να υπολογίσει το π μέχρι και το τελευταίο ψηφίο.  

  “… Κανείς δεν ξέρει αν ο Όιλερ γνώριζε ή όχι ότι ο Τζόουνς είχε χρησιμοποιήσει το π, αλλά αυτό δεν έχει μεγάλη σημασία. Ενώ η επιρροή του Τζόουνς στάθηκε μικρή, ο Όιλερ ήταν σπουδαίος και μετέδωσε και στους άλλους τη χρήση του συμβόλου π. … Στη συνέχεια, όταν ο Όιλερ χρησιμοποίησε το συμβολισμό π στο έργο του Introductio in Analysin Infinitorum (που δημοσιεύτηκε το 1748), η χρήση του συμβόλου γενικεύτηκε.”

 Όταν ο Ουίλιαμ Σανκς πρωτοδημοσίευσε τα 707 ψηφία του το 1873, τα λάθη του δεν βρίσκονταν μόνο στους υπολογισμούς του. Ακόμη και πριν το περιβόητο 527ο ψηφίο υπήρχαν τυπογραφικά λάθη που έγιναν από το στοιχειοθέτη στο 326ο ψηφίο και άλλα παρόμοια λάθη που έγιναν στα ψηφία 460-462 και 513-515.

 1997 : Ο Κάναντα και ο Τακαχάσι υπολόγισαν 51,5 δισεκατομμύρια (3×234) ψηφία με ένα Hitachi SR2201 σε λίγο περισσότερο από 29 ώρες.

 “… Πράγματι, ακόμη και ο πιο σχολαστικός μηχανικός δεν θα χρειαζόταν ποτέ περισσότερα από 7 ψηφία του π, κι ένας φυσικός δεν θα χρησιμοποιούσε περισσότερα πό 15 ή 20. …”

 Ωστόσο, ενώ η σειρά Γκρέκορι-Λάιμπνιτζ είναι εντυπωσιακή για την απλότητα της καθώς και για όσα αποκαλύπτει για την φύση του π, αποδεικνύεται ουσιαστικά άχρηστη στον υπολογισμό ψηφίων. Απαιτούνται 300 όροι της σειράς για να υπολογιστούν μόνο 2 δεκαδικά ψηφία του π, και χιλιάδες άλλοι για να αποκτήσει η σειρά ουσιαστική χρησιμότητα. ………. Για τους 500.000 όρους θα πάρουμε 30 ψηφία του π με Η/Υ. Δυστυχώς ο υπολογισμός δεν είναι απόλυτα σωστός με μεγάλο ποσοστό διακριτών ψηφίων λάθος…. 

 Ο Ντέιβιντ Τσουντνόφσκι και οι γονείς του κακοποιήθηκαν σωματικά από πράκτορες της KGB. ……….. .. Οι αδερφοί Τσουντνόφσκι υπολόγισαν 1 δισεκατομμύριο ψηφία………..

 

Η χαρά του π. / Ντέιβιντ Μπλάτνερ 2001

 

Αεί ο Θεός οΜέγας γεωμετρεί. 3,14159…

ΠΛΑΤΩΝ

2002: Ο Δρ Κάναντα και η ομάδα του, με έναν HITACHI SR8000/MPP,  ανακαλύπτουν 1,2411 τρισεκατομμύρια ψηφία του π. (Ιαπωνία)

http://www.joyofpi.com/pifacts.html  / 2009

http://www.super-computing.org/pi_current.html / 2005

2009: Η ερευνητική ομάδα του κέντρου υπολογιστικών συστημάτων του πανεπιστημίου Tsukuba με έναν υπερυπολογιστή T2K  ανακαλύπτουν 2.576.980.370.000 ψηφία του π, και κάνουν νέο ρεκόρ. (Ιαπωνία)

http://www.tsukuba.ac.jp/english/topics/20090821100620.html /2009 

2010: 5 τρισεκατομμύρια ψηφία ανακαλύπτονται από τον Αλεξάντερ Γη και τον Σινκερού Κοντό με έναν ισχυρό 12 πύρηνο προσωπικό υπολογιστή σε 77,611 ώρες (77 μέρες 14 ώρες 40 λεπτά και 15 δεύτερα), χρησιμοποιώντας αυτήν την φορά την αλγεβρική φόρμουλα του Κουντνόβσκι. Τα  10 τελευταία ψηφία είναι 9484283852.

(Ιαπωνία)

http://www.numberworld.org/misc_runs/pi-5t/details.html / 2010 

2013: 10 τρισεκατομμύρια ψηφία ανακαλύπτονται από τον Αλεξάντερ Γη και τον Σινκερού Κοντό με έναν ισχυρό 12 πύρηνο προσωπικό υπολογιστή, περίπου ίδιο με τον προηγούμενο αλλά με μεγαλύτερες αποθηκευτικές διατάξεις, σε  371 ημέρες, 4ώρες και 40 λεπτά.

(Ιαπωνία)

http://www.numberworld.org/misc_runs/pi-10t/details.html /2013

Στατιστικά στοιχεία: 

Τόσο για την ανακάλυψη του αριθμού, όσο και για την κατανόηση της φύσης του με στατιστικά στοιχεία χρησιμοποιούνται υπολογιστες που κάνουν χρονοβόρους υπολογισμούς πάνω στο δεκαδικό μέρος του π. Παραθέτουμε στατιστικά στοιχεία της εμφάνισης ψηφίων του π.

ΑΠΟΘΗΚΕΥΣΤΕ ΤΙΣ ΠΑΡΑΚΑΤΩ ΕΙΚΟΝΕΣ ΜΕ ΤΑ  ΣΤΑΤΙΣΤΙΚΑ ως 10.000.000 δεκαδικά ψηφία του π.

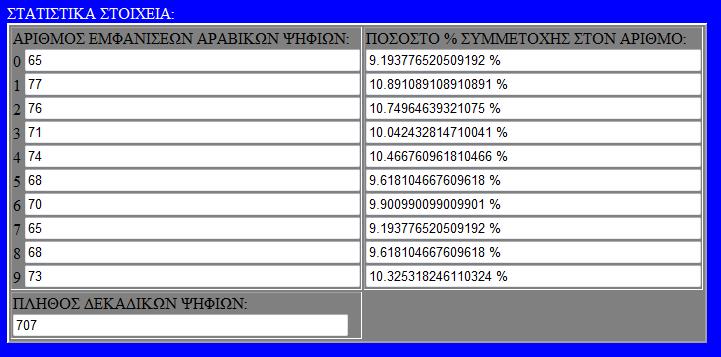
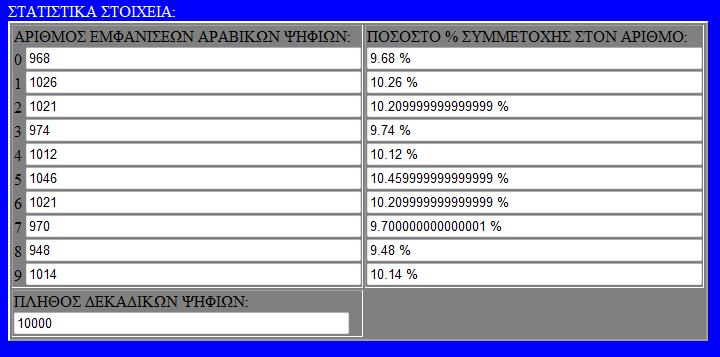
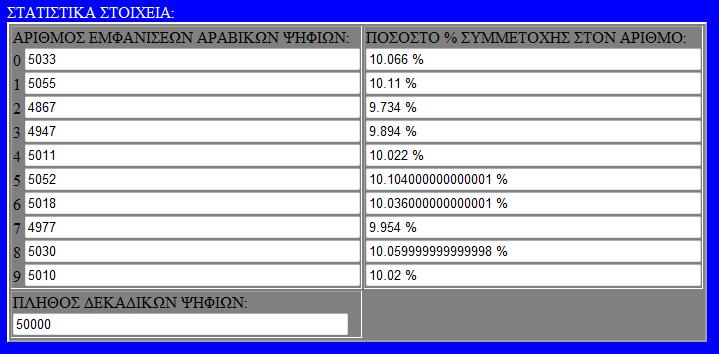
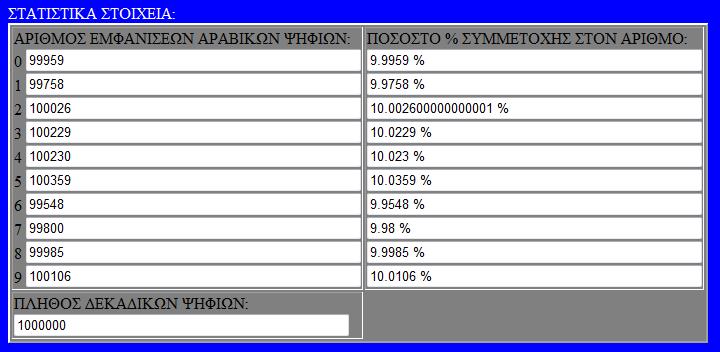
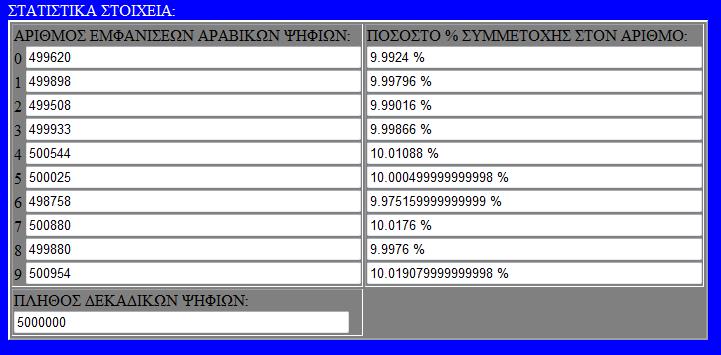
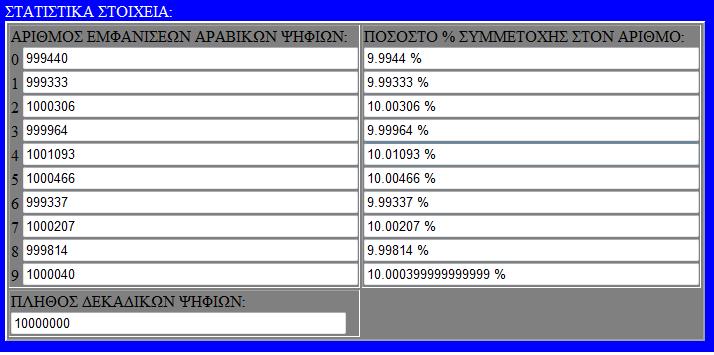
Αριθμοί + Πράξεις / στατιστικό εργαλείο δεκαδικών αριθμών 2009

http://www.jx90.com/download/pi.html / Δεδομένα για τις τελευταίες μετρήσεις (Ενδείκνυται για χρήστες xDSL συνδέσεων)

“Αποζητούμε να ανακαλύψουμε τις επι μέρους δομές του κόσμου που μας περιβάλλει γιατί έτσι μόνο μπορούμε να δώσουμε νόημα σε οτιδήποτε, συμπεριλαμβανομένου του ίδιου μας του εαυτού. … Καθώς τα ψηφία του π απλώνονται στο άπειρο, η ροή τους φαίνεται τελείως τυχαία. Σα να ρίχνουμε ένα δεκάπλευρο ζάρι: υπάρχει μία πιθανότητα στις δέκα ο επόμενος αριθμός που θα προκύψει να είναι το 3 ή το 7 ή το 0. Αλλά τα ψηφά του π δεν είναι απλώς ένας κοσμικός θόρυβος χωρίς νόημα’ αν αλλάξουμε ένα και μόνο ψηφίο-ας πούμε ότι αντικαθιστούμε ένα 4με 9-, δεν έχουμε πια το π. Ο λόγος της περιφέρειας ενός κύκλου προς τη διάμετρο του απαιτεί ακρίβεια.“

 Η χαρά του π. / Ντέιβιντ Μπλάτνερ 2001

Yπολογισμός π με υπολογιστή (wikipedia):

http://en.wikipedia.org/wiki/Pi#Computation_in_the_computer_age

Υπολογιστική αλγεβρική φόρμουλα π (2002):

\pi=\48\tau o\xi\epsilon\phi\left(\frac{1}{49}\right)

\ +128\tau o\xi\epsilon\phi\left(\frac{1}{57}\right)

\ -20\tau o\xi\epsilon\phi\left(\frac{1}{239}\right)

\+48\tau o\xi\epsilon\phi\left(\frac{1}{110443}\right)

1982/ Κ. Τακάνο.

Φόρμουλα αλγεβρικής επαλήθευσης π (2002):

\magenta \pi=\176\tau o\xi\epsilon\phi\left(\frac{1}{57}\right)

\magenta\ +28\tau o\xi\epsilon\phi\left(\frac{1}{239}\right)

\magenta\ -48\tau o\xi\epsilon\phi\left(\frac{1}{682}\right)

\magenta\ +96\tau o\xi\epsilon\phi\left(\frac{1}{12943}\right)

1896/ Φ. Σ. Μ. Σρόεμερ

Γνωρίζοντας ότι:

\blue\tau o\xi\epsilon\phi\left(\chi\right)=\int_0^x\frac{1\,dz}{1+z^2}

 

\blue \ =\left .\frac{i \ln\left(\omega + i\right)}{2} - \frac{i \ln\left(\omega - i\right)}{2}\right|_{\omega = 0, \chi}

\blue \ =\left .,5i\ln\left(\frac{\omega + i}{\omega -i}\right)\right|_{\omega = 0, \chi}

(Α)

\blue \ = \left. i\ln\left(\frac{\omega + i}{\sqrt{\omega + 1}}\right)\right|_{\omega = 0, \chi}

(Α 2) 

και

\green\tau o\xi\epsilon\phi\left(\frac{1}{x}\right)=\frac{\pi}{2} -\tau o\xi\epsilon\phi\left(\chi\right)

Αν x>0

(Β)

η αλγεβρική σχέση του Τακάνο απλοποιείται περισσότερο, με βάση τον τύπο (Β), ως εξής:

\red\pi=\frac{48\tau o\xi\epsilon\phi\left(\49\right)+128\tau o\xi\epsilon\phi\left(\57\right)-20\tau o\xi\epsilon\phi\left(\239\right)+48\tau o\xi\epsilon\phi\left(\110443\right)}{101}

και χρησιμοποιώντας ένα scientific υπολογιστή χειρός για το \blue\tau o\xi\epsilon\phi\left(\chi\right), \green \tan^{-1}\left(\chi\right)

μπορούμε να πάρουμε την τιμή του π. Αν χρησιμοποιήσουμε τον τύπο (Α) θα πρέπει να γνωρίζουμε την συνάρτηση που η παράγωγος της είναι η συνάρτηση που εμφανίζεται στο ολοκλήρωμα, όπως φαίνεται στο δεύτερο σκέλος. Ο τελευταίος τύπος κάνει οικονομία πράξεων μια και ο υπολογισμός είναι ευάλωτος σε διαδιδόμενο υπολογιστικό σφάλμα και από την άλλη σε οδηγεί σε οικονομία πράξεων δηλ. στην μη σπατάλη υπολογιστιστικής ισχύος. Μια πιο απλοποιημένη μορφή είναι ο τύπος (Α2). Αν οι τύποι (Α) και (Α2) δεν μπορούν να μετασχηματιστούν ώστε να εξαλειφθεί το φαντασικό μέρος δεν μπορούν να έχουν πρακτική υπολογιστική αξία. Δεδομένο είναι ότι το αποτέλεσμα είναι πραγματικός. Ίσως θα έπρεπε να στραφούμε τότε στον τύπο του Όιλερ όπου το τοξεφ(χ)/arctan(x) δίνεται ως άπειρο άθροισμα:

\green\tau o\xi\epsilon\phi\left(x\right)= \frac{x}{1+x^2} \sum_{n=0}^\infty \prod_{k=1}^n \frac{2k x^2}{(2k+1)(1+x^2)}

Tώρα εδώ θα πρέπει να σκεφτούμε τι εννούμε άπειρο για τους υπολογισμούς μας. Ίσως ένα αυθαίρετο n =1035 (μέγιστη διάσταση παρατηρήσιμου σύμπαντος) να ήταν αρκετό…. Η αλήθεια είναι ότι η λήψη μιας πολύ μεγάλης τιμής (σταθερά) ως άπειρο θα επηρέαζε και την ακρίβεια του δεκαδικού μέρους που θέλουμε να πάρουμε και θα οδηγούμαστε σε λάθος υπολογισμούς. Η δε τιμή που θα υπολογίζαμε θα ήταν παραπλήσια αυτής που θέλουμε να υπολογίσουμε, αλλά όχι αυτή!!!! ….. ;;;;

Μερικά μικρά συμπεράσματα (παράπλευρες απώλειες):

– Ένας πολλαπλασιασμός, κατά τον υπολογισμό του π, είναι λιγότερο αδειφάγος σε πόρους του συστήματος από μια διαίρεση, πόσο μάλλον μια πρόσθεση ή μια αφαίρεση. Αν έχουμε διαιρέσεις, π.χ. δια 2, το καλύτερο που έχουμε να κάνουμε είναι να πολλαπλασιάσουμε με 0,5 ή αν έχουμε διαίρεση δια κ καλύτερα είναι να βρούμε το πηλίκο του 1/κ σε προγενέστερο χρόνο και να το πολλαπλασιάσουμε κατά τους υπολογισμούς μας με την αλγεβρική έκφραση που έχουμε υπολογίσει.

– Ουσιαστικά το κομπιουτεράκι, που όλοι έχουμε, για τον υπολογισμό του τοξεφ(χ), τοξσυν(χ), τοξημ(χ) κάνει αναγωγή από την μια στην άλλη και συγκεκριμένα στην πιο εύκολα υπολογιζόμενη. Το ίδιο γίνεται και στο ημ(χ), συν(χ), εφ(χ), σφ(χ). Άλλα το ίδιο γίνεται και μεταξύ των τριγωνομετρικών εξισώσεων και των αντιστρόφων τριγωνομετρικών εξισώσεων. Δεν περιέχει πίνακα έτοιμων αποτελεσμάτων.

– Αν τα 10 ψηφία, με πιθανότητα εμφάνισης 10% έκαστο, στο MsWord, μέγεθος γραμμάτων 10, γραμματοσειρά Times New Roman, και ανάλυση 1024 x 768, καταλαμβάνουν χώρο περίπου 1,8 cm, τα 2.576.980.370.000 φηφία που ανακαλύφτηκαν το 2009, έχουν μήκος περίπου 4.638.564,666 km!!!!! Είναι βέβαιο ότι η εκτύπωση του δεκαδικού μέρους είναι μια πάρα πολύ ακριβή διαδικασία και αρκετά ψυχοφθόρα και ίσως να μην τελείωνε ποτέ από κάποια από τις αλλαγές μελάνης!!!!! Το τελικό κείμενο με τα δεκαδικά ψηφία θα ήταν εκτυπωμένο σε 517.465.937 & 3/4 σελίδες, δεδομένο ότι μια σελίδα στο MsWord με μέγεθος χαρακτήρων 10,  γραμματοσειρά Times New Roman, και προεπιλεγμένα περιθώρια καταλαμβάνεται από 4980 ψηφία!!!!! Από την άλλη δεδομένου ότι ένας αριθμός καταλαμβάνει χώρο 1 byte, το σύνολο των δεκαδικών ψηφίων που ανακαλύφτηκαν το 2009 καταλαμβάνει χώρο τουλάχιστον 2,343 Tera bytes και απαιτεί την χρήση σκληρού δίσκου, ή δίσκων, πολύ μεγάλης χωρητικότητας!!!!!

Το συνδικάτο των ΜΑΘΗΜΑΤΙΚΩΝ

Εν κατακλείδι..

Στατιστικά στο 97,0128% του αριθμού που ανακαλύφτηκε το 1997.

http://www.cecm.sfu.ca/~jborwein/Kanada_50b.html

Yasumasa KANADA and Daisuke TAKAHASHI (1997)

Happy the globalized new world record of pi!!!!

Ετικέτες:

Εισαγωγή.

Σεπ 08 21

Αναρτήθηκε από ΝΙΚΟΣ ΠΑΝΟΥΣΟΠΟΥΛΟΣ. Κατηγορία: Γενικά | Κλειστά Σχόλια

Λίγα λόγια:
Το blog δεν είναι διαφημιστικό. Απλά κάνει μια απλή αναφορά πληροφοριών σε πράγματα που γράφτηκαν, σε μια μικρή έρευνα που έγινε, και σε μη κερδοσκοπικά εργαλεία, με πλήρεις δυνατότητες, που δημιουργήθηκαν (μπορεί να κρύβουν λάθη). Τις εφαρμογές αυτές μπορείτε να τις κρατήσετε, αν τις αποθηκεύσετε στον Η/Υ σας, χωρίς να συνδέεστε στο διαδίκτυο, αν βέβαια υπάρχει ενδιαφέρον.

Κάτι που γράφτηκε:
“Είχα μια μανία με το Π=3,14. Έχω γράψει κάποια πράγματα στο βιβλίο μου στην “Τελική Ευθύνη” για το Π ως μετασχηματιστή του κύκλου της φύσης στο τετράγωνο της λογικής. Γι’ αυτό πηγαίνω και ξαναπηγαίνω στην Πολιόχνη της Λήμνου, στα πρώτα τετράγωνα σπίτια μετά τις κυκλικές καλύβες.”

Γιώργος Πασχαλίδης – ΤΑ ΝΕΑ / Τετάρτη 1 Αυγούστου 2001

 

Το πολυχρηστικό ορατό φάσμα του π σε παρελθόντα χρόνο:

… υλοενέργεια σε ένα στιγμιότυπο του πολυμεταβλητού χωροχρόνου.

ΤΑ ΝΕΑ – ένθετο: ΟΙ ΑΓΝΩΣΤΟΙ ΘΗΣΑΥΡΟΙ ΤΗΣ ΕΛΛΑΔΑΣ / 2008  

Ορισμός π (ΜΑΘ.):
το πηλίκο της περιφέρειας ενός κύκλου δια της διαμέτρου του κύκλου, ισούται κατά προσέγγιση με 3,1416.

Το παπυράκι-ΕΓΚΥΛΟΠΑΙΔΙΚΟ ΛΕΞΙΚΟ / 2003

Συμπληρωματικός προσδιορισμός:
Ο λόγος αυτός είναι αριθμός σταθερός και ασύμμετρος υπερβατικός, με άπειρα μη περιοδικά δεκαδικά ψηφία και γι’ αυτό ώς τιμή του λαμβάνεται κατά προσέγγιση  3,14.

ΧΑΡΗ ΠΑΤΣΗ – Εγκυκλοπαίδεια / 1980

Σημ:
υπερβατικός: αριθμός που δεν είναι ρίζα αλγεβρικής εξίσωσης με ακέραιους συντελεστές.
περιοδικός: αριθμός που το δεκαδικό του μέρος επαναλαμβάνεται.

Απομνημόνευση μεγάλης κλίμακας ακριβείας δεκαδικών ψηφίων:
Για την απομνημόνευση πολλών δεκαδικών ψηφίων του αριθμού π, χρησιμοποιήθηκαν από ξένους και Έλληνες διάφορα τετράστιχα. Ο αριθμός των γραμμάτων κάθε λέξης του τετραστίχου είναι το αντίστοιχο ψηφίο του αριθμού π:

“Αεί (3 , ) ο (1) θεός (4) ο (1) μέγας (5) γεωμετρεί (9).
Το (2) κύκλου (6) μήκος (5) ίνα (3) ορίσει (5) διαμέτρω (8), παρήγαγεν (9) αριθμόν (7) απέραντον (9) και (3) όν (2) φευ (3)! ουδέποτε (8) όλον (4) θνητοί (6) θα (2) ευρώσι (6).”

Ν. Χατζηδάκης /ΧΑΡΗ ΠΑΤΣΗ Εγκυκλοπαίδεια – 1980

O υπολογισμός του:
Ο μεγάλος μαθηματικός Λάιμνιτζ προτείνει τον τρόπο υπολογισμού του π (pi στα Λατινικά) με το άθροισμα της σειράς:

\red \frac {\pi}{4}=\1-\frac {1}{2}+\frac {1}{3}-\frac {1}{4}+\frac{1}{5}-\frac {1}{6}+\frac {1}{7}-\frac {1}{8}+\frac{1}{9}-\frac{1}{10}+\frac{1}{11}-\frac{1}{12}+...

ή αλλιώς:

\green \exists\pi\in\Re^{\ast +} : \;\;\;\;\;\pi = \4\sum_{\nu=1}^{+\infty}\frac {{(-1)}^{(\nu+1)}}{\nu}\;\;\;,\;\;\;\nu\in N^{\ast}

 

Λίγη Ιστορία:
>> Ο Αρχιμήδης έδειξε ότι η τιμή του π περιλαμβάνεται μεταξύ των αριθμών:

\red\3\;\frac {10}{71}<\pi <3\;\frac {1}{7}

όπου:

\green\3\;\frac {10}{71}=

3,140845070422535211267605633802816901408450704225352112676…

και

\blue\3\;\frac {1}{7}=

3,1428571428571428571428571428571428571428571428571428571428…

Είναι προφανές ότι και οι δύο αριθμοί είναι περιοδικοί.

>> Οι Κινέζοι την δεύτερη πεντηκονταετία του 5ου αιώνα προσέγγισαν το π με τον λόγο:

\red\pi = \frac {355}{113}=

3,1415929203539823008849557522123893805309734513274336283185840707964601

769911504424778761061946902654867256637168141592920353982300884955752212

3893805309734513274336283185840707964601769911504424778761…

Είναι προφανές ότι ο αριθμός είναι περιοδικός, και οδηγήθηκαν σε σφάλμα:

\green\epsilon \simeq

0,000000266764189062422312368932886496333804051952327807343639478488643

7707049414438498413…

συγκεκριμένα:

\blue\epsilon\simeq

0,0000084913678658370862584021992894198817243148000695671184197184218816

9938127426016… % του π

πράγμα που σημαίνει ότι υπολόγισαν μεγαλύτερη τιμή από την πραγματική.

>> Ο Γουίλλιαμ Σάνκς το 1873 υπολόγισε 707 από τα δεκαδικά ψηφία του π, αριθμός που εκτίθεται στο Μέγαρο των Ανακαλύψεων (Palais de la Decouverte) στο Παρίσι. Προφανώς σε τέτοια μεγάλης κλίμακας ακρίβεια θα μπορούσε να παρατηρήσει πιθανή περιοδικότητα, αν βέβαια του δίνονταν στα 707 ψηφία.

>> Σήμερα με την χρήση των Η/Υ έχουν υπολογιστεί εκατομμύρια και δισεκατομμύρια δεκαδικά ψηφία του π. Προφανώς η ανακάλυψη περιοδικότητας ακόμη και στο δισεκατομμυριοστό (;) δεκαδικό ψηφίο είναι ένας από τους στόχους των εργασιών. Σύμφωνα με την θεωρεία των πιθανοτήτων (σε κάποιο ενδιάμεσο αποτελέσμα πράξεων) είναι ένα από τα ενδεχόμενα. Μόνο που η ανακάλυψη περιοδικότητας (προβλεψιμότητας) θα υποβίβαζε τον π από θετικό πραγματικό αριθμό σε θετικό ρητό και η ανακάλυψη των ψηφίων θα ήταν μια προσέγγιση της πραγματικής τιμής του  π ανάλογη με το παρελθόν…;;;…;;;………….

ΧΑΡΗ ΠΑΤΣΗ – Εγκυκλοπαίδεια / 1980
Ενότητα – Eργαλείο Αριθμοί + Πράξεις  / 2007




Τα 1.000.000 δεκαδικά ψηφία (από τα δισεκατομμύρια που έχουν ανακαλυφθεί) του π δίνονται στην πιο κάτω διεύθυνση:
http://www.exploratorium.edu/pi/Pi10-6.html

Διαδίκτυο (keyword: pi digits)/ 2009

Ετικέτες:

Το π. ( ΛΑΤΙΝΙΣΤΙ: pi )

Απρ 08 22

Αναρτήθηκε από ΝΙΚΟΣ ΠΑΝΟΥΣΟΠΟΥΛΟΣ. Κατηγορία: Γενικά | Κλειστά Σχόλια

    Ο υπερβατικός π.
Απόσπασμα από το βιβλίο: το Θεώρημα του παπαγάλου, σελ. 488.

“Είναι αλήθεια ότι η μνήμη ενεργοποιείται όταν ξαναβρεθεί κανείς στο μέρος που συνέβησαν τα γεγονότα!
-“Η πρώτη από τις επιστήμες που ξεπρόβαλε σπό την άχρωμη θάλασσα του Αφηρημένου, φορά το σάρκικνο ένδυμα της Αφροδίτης αναδυόμενης από την ανάσα του θαλασσινού αφρού. Κάτω από ένα θόλο, εμπνευσμένο από το διάκοσμο μιας κυβιστικής ταινίας, απλώνεται σαν μια κορδέλα η σειρά των 700 πρώτων δεκαδικών ψηφίων του π.”
Είχαν φτάσει στον προορισμό τους! Ο ναός του π. Μια αίθουσα, μοναδική στον κόσμο, που είχε κάνει γενιές και γενιές νέων ανθρώπων να ονειροπολήσουν. Και τους έκανε ακόμα να ονειροπολούν, αν έκρινε κανείς από το πλήθος των εφήβων που στριμώχνονταν μέσα στην αίθουσα. Την αίθουσα που, φυσικά ήταν στρογγυλή!
Γύρω γύρω στην αίθουσα, σε μια κυκλική λωρίδα, ήταν γραμμένα τα ονόματα διάσημων μαθηματικών. Από πάνω, κάτω από έναν φωτισμένο σφαιρικό θόλο, βρισκόντουσαν τα ψηφία. Σε ομάδες των δέκα, εναλλάξ κόκκινα και μαύρα, τα πρώτα 707 δεκαδικά ψηφία του π.
Εντυπωσιασμένος από αυτο το αριθμητικό γράφιτι, ο Μάξ έριξε μια ματιά στο αρχικό 3, πήδηξε την υποδιαστολή κι άρχισε να διαβάζει: 1415926535, σε κόκκινο, 8979323846 σε μαύρο, 2643383279 σε κόκκινο, 502… επιτάχυνε την ανάγνωση, κόκκινα, μαύρα, κόκκινα. Τέλος του πρώτου κύκλου. Είχε φτάσει κάτω από το αρχικό 3, μαύρα, κόκκινα. Ο δρομέας των δεκαδικών! Επιτάχυνε κι άλλο, μαύρο, κόκκινο, μαύρο, κόκκινο όπως στη ρουλέττα. Τα κατάμαυρα μάτια του σαν την μπίλια της ρουλέττας πηδούσαν από αριθμό σε αριθμό. Κέρδισε, έχασε, κέρδισε! Τα μάτια του γέμισαν δάκρυα. Άραγε που να ήταν ο Αμέλλων αυτή τη στιγμή; Μαύρο, κόκκινο, μαύρο, κόκκινο σαν τις άκρες των φτερών του.”

Φυσικά πρόκειται για το κτίριο του Μεγάρου των Ανακαλύψεων (Palais de la Decouverte) στο Παρίσι όπου εκτίθενται τα 707 δεκαδικά ψηφία του π (αναφέρεται στο βιβλίο).

Σήμερα με την χρήση των Η/Υ (πολύπλοκοι αλγόριθμοι υψηλής νοημοσύνης σε μηχανές υψηλών δυνατοτήτων) έχουν ανακαλυφτεί χιλιάδες ή και εκατομμύρια δεκαδικά ψηφία του π ΧΩΡΙΣ πρακτική αξία. Βέβαια πίσω απ’ αυτές τις υπέροχες μηχανές κρύβονται άνθρωποι που την εικόνα τους και την νοημοσύνη τους τους εμφυτεύουν. Όμως δεν διατίθενται ευρέως και τα υψηλής ακρίβειας εργαλεία που θα βοηθούσαν σε ακριβέστερους υπολογισμούς. Ίσως και η τιμή 3,14 αποτελεί μια σταθερά, κατά προσέγγιση, μέτρησης του φυσικού μας κόσμου.

Η χρήση του:

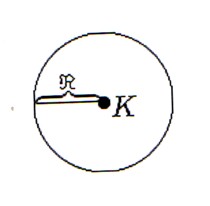
Και όπως είναι γωστό από την γεωμετρία σε επίπεδο κύκλο 2 διαστάσεων με δεδομένη ακτίνα R το εμβαδό (Εμβ) της επιφάνειας που ορίζει και περιέχει και η περίμετρος (Περ) δίνονται αντίστοιχα από τους παρακάτω τύπους:

\red E\mu\beta=\pi\ R ^2

\green \Pi\epsilon\rho=\ 2\pi\ R

Και για σφαίρα στον τρισδιάστατο χώρο με δεδομένη ακτίνα R το εμβαδό (Εμβ) της εξωτερικής επιφάνειας και ο όγκος (Όγκ) που καταλαμβάνει δίνονται αντίστοιχα από τους παρακάτω τύπους:

\blue E\mu\beta=\ 4\pi\ R^2

\black 'O\kappa\gamma=\frac{4}{3}\pi\ R^3

Ετικέτες:

Οι τιμές του π.

Απρ 08 22

Αναρτήθηκε από ΝΙΚΟΣ ΠΑΝΟΥΣΟΠΟΥΛΟΣ. Κατηγορία: Γενικά | Κλειστά Σχόλια

 

Ο υπερβατικός π:

Διαδίκτυο. : 1.000.000 ψηφία. (<< κλίκ εδώ)

Mέγαρο των ανακαλύψεων.: Palais de la decouverte. – 707 ψηφία (<< κλίκ εδώ)

Βιβλίο: Το Θεώρημα του παπαγάλου – ΝΤΕΝΙ ΓΚΕΤΖ – σελ. 488: 3,141592653589793238462643383279502

Αριθμομηχανή των windows: 3,1415926535897932384626433832795

scientific κομπιουτεράκι: 3,141592654

Βιβλίο μαθηματικών Λυκείου: 3,14159

Βιβλίο μαθηματικών Γυμνασίου: 3,14

Ετικέτες:

Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH