Στο επεισόδιο του Σταρ Τρεκ “Λύκος στο κοπάδι“ ο Σποκ ματαιώνει τα σατανικά σχέδια ενός υπολογιστή, ζητώντας του να υπολογίσει το π μέχρι και το τελευταίο ψηφίο.  

  “… Κανείς δεν ξέρει αν ο Όιλερ γνώριζε ή όχι ότι ο Τζόουνς είχε χρησιμοποιήσει το π, αλλά αυτό δεν έχει μεγάλη σημασία. Ενώ η επιρροή του Τζόουνς στάθηκε μικρή, ο Όιλερ ήταν σπουδαίος και μετέδωσε και στους άλλους τη χρήση του συμβόλου π. … Στη συνέχεια, όταν ο Όιλερ χρησιμοποίησε το συμβολισμό π στο έργο του Introductio in Analysin Infinitorum (που δημοσιεύτηκε το 1748), η χρήση του συμβόλου γενικεύτηκε.”

 Όταν ο Ουίλιαμ Σανκς πρωτοδημοσίευσε τα 707 ψηφία του το 1873, τα λάθη του δεν βρίσκονταν μόνο στους υπολογισμούς του. Ακόμη και πριν το περιβόητο 527ο ψηφίο υπήρχαν τυπογραφικά λάθη που έγιναν από το στοιχειοθέτη στο 326ο ψηφίο και άλλα παρόμοια λάθη που έγιναν στα ψηφία 460-462 και 513-515.

 1997 : Ο Κάναντα και ο Τακαχάσι υπολόγισαν 51,5 δισεκατομμύρια (3×234) ψηφία με ένα Hitachi SR2201 σε λίγο περισσότερο από 29 ώρες.

 “… Πράγματι, ακόμη και ο πιο σχολαστικός μηχανικός δεν θα χρειαζόταν ποτέ περισσότερα από 7 ψηφία του π, κι ένας φυσικός δεν θα χρησιμοποιούσε περισσότερα πό 15 ή 20. …”

 Ωστόσο, ενώ η σειρά Γκρέκορι-Λάιμπνιτζ είναι εντυπωσιακή για την απλότητα της καθώς και για όσα αποκαλύπτει για την φύση του π, αποδεικνύεται ουσιαστικά άχρηστη στον υπολογισμό ψηφίων. Απαιτούνται 300 όροι της σειράς για να υπολογιστούν μόνο 2 δεκαδικά ψηφία του π, και χιλιάδες άλλοι για να αποκτήσει η σειρά ουσιαστική χρησιμότητα. ………. Για τους 500.000 όρους θα πάρουμε 30 ψηφία του π με Η/Υ. Δυστυχώς ο υπολογισμός δεν είναι απόλυτα σωστός με μεγάλο ποσοστό διακριτών ψηφίων λάθος…. 

 Ο Ντέιβιντ Τσουντνόφσκι και οι γονείς του κακοποιήθηκαν σωματικά από πράκτορες της KGB. ……….. .. Οι αδερφοί Τσουντνόφσκι υπολόγισαν 1 δισεκατομμύριο ψηφία………..

 

Η χαρά του π. / Ντέιβιντ Μπλάτνερ 2001

 

Αεί ο Θεός οΜέγας γεωμετρεί. 3,14159…

ΠΛΑΤΩΝ

2002: Ο Δρ Κάναντα και η ομάδα του, με έναν HITACHI SR8000/MPP,  ανακαλύπτουν 1,2411 τρισεκατομμύρια ψηφία του π. (Ιαπωνία)

http://www.joyofpi.com/pifacts.html  / 2009

http://www.super-computing.org/pi_current.html / 2005

2009: Η ερευνητική ομάδα του κέντρου υπολογιστικών συστημάτων του πανεπιστημίου Tsukuba με έναν υπερυπολογιστή T2K  ανακαλύπτουν 2.576.980.370.000 ψηφία του π, και κάνουν νέο ρεκόρ. (Ιαπωνία)

http://www.tsukuba.ac.jp/english/topics/20090821100620.html /2009 

2010: 5 τρισεκατομμύρια ψηφία ανακαλύπτονται από τον Αλεξάντερ Γη και τον Σινκερού Κοντό με έναν ισχυρό 12 πύρηνο προσωπικό υπολογιστή σε 77,611 ώρες (77 μέρες 14 ώρες 40 λεπτά και 15 δεύτερα), χρησιμοποιώντας αυτήν την φορά την αλγεβρική φόρμουλα του Κουντνόβσκι. Τα  10 τελευταία ψηφία είναι 9484283852.

(Ιαπωνία)

http://www.numberworld.org/misc_runs/pi-5t/details.html / 2010 

2013: 10 τρισεκατομμύρια ψηφία ανακαλύπτονται από τον Αλεξάντερ Γη και τον Σινκερού Κοντό με έναν ισχυρό 12 πύρηνο προσωπικό υπολογιστή, περίπου ίδιο με τον προηγούμενο αλλά με μεγαλύτερες αποθηκευτικές διατάξεις, σε  371 ημέρες, 4ώρες και 40 λεπτά.

(Ιαπωνία)

http://www.numberworld.org/misc_runs/pi-10t/details.html /2013

Στατιστικά στοιχεία: 

Τόσο για την ανακάλυψη του αριθμού, όσο και για την κατανόηση της φύσης του με στατιστικά στοιχεία χρησιμοποιούνται υπολογιστες που κάνουν χρονοβόρους υπολογισμούς πάνω στο δεκαδικό μέρος του π. Παραθέτουμε στατιστικά στοιχεία της εμφάνισης ψηφίων του π.

ΑΠΟΘΗΚΕΥΣΤΕ ΤΙΣ ΠΑΡΑΚΑΤΩ ΕΙΚΟΝΕΣ ΜΕ ΤΑ  ΣΤΑΤΙΣΤΙΚΑ ως 10.000.000 δεκαδικά ψηφία του π.

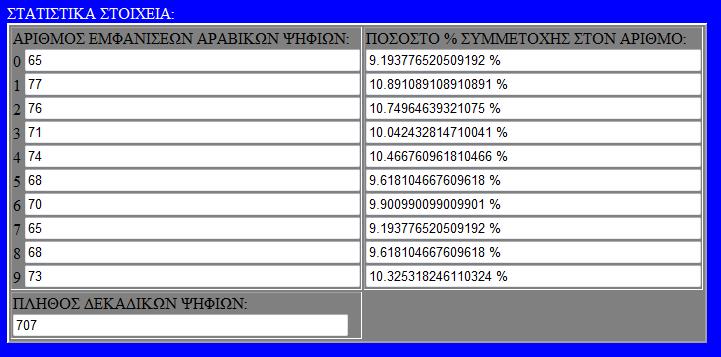
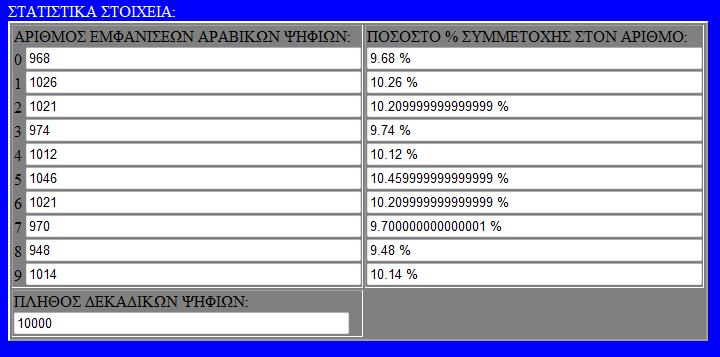
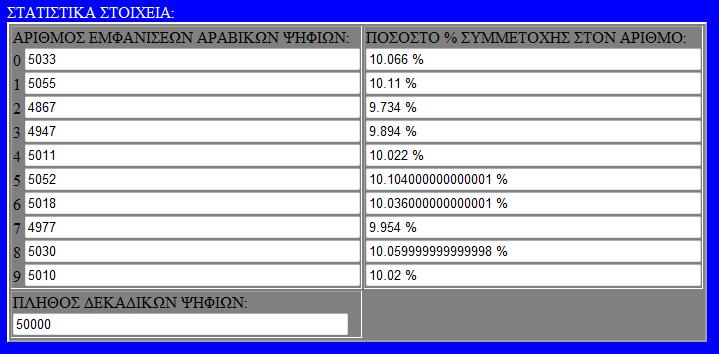
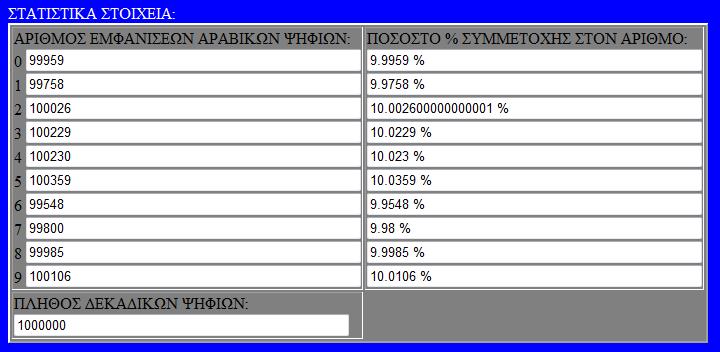
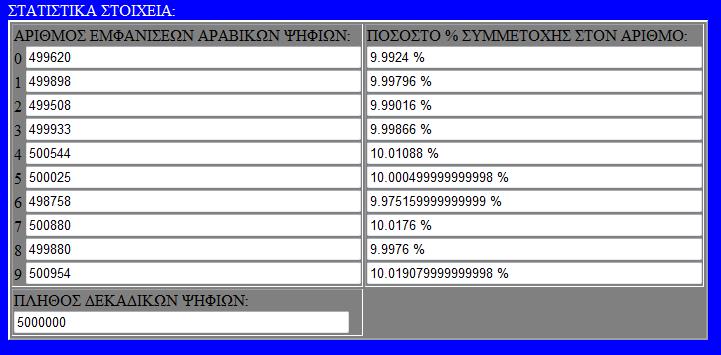
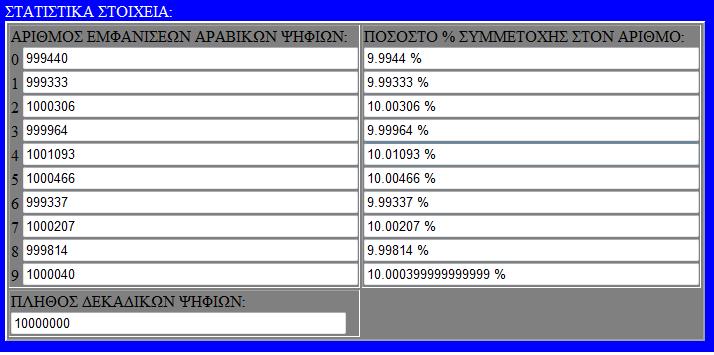
Αριθμοί + Πράξεις / στατιστικό εργαλείο δεκαδικών αριθμών 2009

http://www.jx90.com/download/pi.html / Δεδομένα για τις τελευταίες μετρήσεις (Ενδείκνυται για χρήστες xDSL συνδέσεων)

“Αποζητούμε να ανακαλύψουμε τις επι μέρους δομές του κόσμου που μας περιβάλλει γιατί έτσι μόνο μπορούμε να δώσουμε νόημα σε οτιδήποτε, συμπεριλαμβανομένου του ίδιου μας του εαυτού. … Καθώς τα ψηφία του π απλώνονται στο άπειρο, η ροή τους φαίνεται τελείως τυχαία. Σα να ρίχνουμε ένα δεκάπλευρο ζάρι: υπάρχει μία πιθανότητα στις δέκα ο επόμενος αριθμός που θα προκύψει να είναι το 3 ή το 7 ή το 0. Αλλά τα ψηφά του π δεν είναι απλώς ένας κοσμικός θόρυβος χωρίς νόημα’ αν αλλάξουμε ένα και μόνο ψηφίο-ας πούμε ότι αντικαθιστούμε ένα 4με 9-, δεν έχουμε πια το π. Ο λόγος της περιφέρειας ενός κύκλου προς τη διάμετρο του απαιτεί ακρίβεια.“

 Η χαρά του π. / Ντέιβιντ Μπλάτνερ 2001

Yπολογισμός π με υπολογιστή (wikipedia):

http://en.wikipedia.org/wiki/Pi#Computation_in_the_computer_age

Υπολογιστική αλγεβρική φόρμουλα π (2002):

\pi=\48\tau o\xi\epsilon\phi\left(\frac{1}{49}\right)

\ +128\tau o\xi\epsilon\phi\left(\frac{1}{57}\right)

\ -20\tau o\xi\epsilon\phi\left(\frac{1}{239}\right)

\+48\tau o\xi\epsilon\phi\left(\frac{1}{110443}\right)

1982/ Κ. Τακάνο.

Φόρμουλα αλγεβρικής επαλήθευσης π (2002):

\magenta \pi=\176\tau o\xi\epsilon\phi\left(\frac{1}{57}\right)

\magenta\ +28\tau o\xi\epsilon\phi\left(\frac{1}{239}\right)

\magenta\ -48\tau o\xi\epsilon\phi\left(\frac{1}{682}\right)

\magenta\ +96\tau o\xi\epsilon\phi\left(\frac{1}{12943}\right)

1896/ Φ. Σ. Μ. Σρόεμερ

Γνωρίζοντας ότι:

\blue\tau o\xi\epsilon\phi\left(\chi\right)=\int_0^x\frac{1\,dz}{1+z^2}

 

\blue \ =\left .\frac{i \ln\left(\omega + i\right)}{2} - \frac{i \ln\left(\omega - i\right)}{2}\right|_{\omega = 0, \chi}

\blue \ =\left .,5i\ln\left(\frac{\omega + i}{\omega -i}\right)\right|_{\omega = 0, \chi}

(Α)

\blue \ = \left. i\ln\left(\frac{\omega + i}{\sqrt{\omega + 1}}\right)\right|_{\omega = 0, \chi}

(Α 2) 

και

\green\tau o\xi\epsilon\phi\left(\frac{1}{x}\right)=\frac{\pi}{2} -\tau o\xi\epsilon\phi\left(\chi\right)

Αν x>0

(Β)

η αλγεβρική σχέση του Τακάνο απλοποιείται περισσότερο, με βάση τον τύπο (Β), ως εξής:

\red\pi=\frac{48\tau o\xi\epsilon\phi\left(\49\right)+128\tau o\xi\epsilon\phi\left(\57\right)-20\tau o\xi\epsilon\phi\left(\239\right)+48\tau o\xi\epsilon\phi\left(\110443\right)}{101}

και χρησιμοποιώντας ένα scientific υπολογιστή χειρός για το \blue\tau o\xi\epsilon\phi\left(\chi\right), \green \tan^{-1}\left(\chi\right)

μπορούμε να πάρουμε την τιμή του π. Αν χρησιμοποιήσουμε τον τύπο (Α) θα πρέπει να γνωρίζουμε την συνάρτηση που η παράγωγος της είναι η συνάρτηση που εμφανίζεται στο ολοκλήρωμα, όπως φαίνεται στο δεύτερο σκέλος. Ο τελευταίος τύπος κάνει οικονομία πράξεων μια και ο υπολογισμός είναι ευάλωτος σε διαδιδόμενο υπολογιστικό σφάλμα και από την άλλη σε οδηγεί σε οικονομία πράξεων δηλ. στην μη σπατάλη υπολογιστιστικής ισχύος. Μια πιο απλοποιημένη μορφή είναι ο τύπος (Α2). Αν οι τύποι (Α) και (Α2) δεν μπορούν να μετασχηματιστούν ώστε να εξαλειφθεί το φαντασικό μέρος δεν μπορούν να έχουν πρακτική υπολογιστική αξία. Δεδομένο είναι ότι το αποτέλεσμα είναι πραγματικός. Ίσως θα έπρεπε να στραφούμε τότε στον τύπο του Όιλερ όπου το τοξεφ(χ)/arctan(x) δίνεται ως άπειρο άθροισμα:

\green\tau o\xi\epsilon\phi\left(x\right)= \frac{x}{1+x^2} \sum_{n=0}^\infty \prod_{k=1}^n \frac{2k x^2}{(2k+1)(1+x^2)}

Tώρα εδώ θα πρέπει να σκεφτούμε τι εννούμε άπειρο για τους υπολογισμούς μας. Ίσως ένα αυθαίρετο n =1035 (μέγιστη διάσταση παρατηρήσιμου σύμπαντος) να ήταν αρκετό…. Η αλήθεια είναι ότι η λήψη μιας πολύ μεγάλης τιμής (σταθερά) ως άπειρο θα επηρέαζε και την ακρίβεια του δεκαδικού μέρους που θέλουμε να πάρουμε και θα οδηγούμαστε σε λάθος υπολογισμούς. Η δε τιμή που θα υπολογίζαμε θα ήταν παραπλήσια αυτής που θέλουμε να υπολογίσουμε, αλλά όχι αυτή!!!! ….. ;;;;

Μερικά μικρά συμπεράσματα (παράπλευρες απώλειες):

– Ένας πολλαπλασιασμός, κατά τον υπολογισμό του π, είναι λιγότερο αδειφάγος σε πόρους του συστήματος από μια διαίρεση, πόσο μάλλον μια πρόσθεση ή μια αφαίρεση. Αν έχουμε διαιρέσεις, π.χ. δια 2, το καλύτερο που έχουμε να κάνουμε είναι να πολλαπλασιάσουμε με 0,5 ή αν έχουμε διαίρεση δια κ καλύτερα είναι να βρούμε το πηλίκο του 1/κ σε προγενέστερο χρόνο και να το πολλαπλασιάσουμε κατά τους υπολογισμούς μας με την αλγεβρική έκφραση που έχουμε υπολογίσει.

– Ουσιαστικά το κομπιουτεράκι, που όλοι έχουμε, για τον υπολογισμό του τοξεφ(χ), τοξσυν(χ), τοξημ(χ) κάνει αναγωγή από την μια στην άλλη και συγκεκριμένα στην πιο εύκολα υπολογιζόμενη. Το ίδιο γίνεται και στο ημ(χ), συν(χ), εφ(χ), σφ(χ). Άλλα το ίδιο γίνεται και μεταξύ των τριγωνομετρικών εξισώσεων και των αντιστρόφων τριγωνομετρικών εξισώσεων. Δεν περιέχει πίνακα έτοιμων αποτελεσμάτων.

– Αν τα 10 ψηφία, με πιθανότητα εμφάνισης 10% έκαστο, στο MsWord, μέγεθος γραμμάτων 10, γραμματοσειρά Times New Roman, και ανάλυση 1024 x 768, καταλαμβάνουν χώρο περίπου 1,8 cm, τα 2.576.980.370.000 φηφία που ανακαλύφτηκαν το 2009, έχουν μήκος περίπου 4.638.564,666 km!!!!! Είναι βέβαιο ότι η εκτύπωση του δεκαδικού μέρους είναι μια πάρα πολύ ακριβή διαδικασία και αρκετά ψυχοφθόρα και ίσως να μην τελείωνε ποτέ από κάποια από τις αλλαγές μελάνης!!!!! Το τελικό κείμενο με τα δεκαδικά ψηφία θα ήταν εκτυπωμένο σε 517.465.937 & 3/4 σελίδες, δεδομένο ότι μια σελίδα στο MsWord με μέγεθος χαρακτήρων 10,  γραμματοσειρά Times New Roman, και προεπιλεγμένα περιθώρια καταλαμβάνεται από 4980 ψηφία!!!!! Από την άλλη δεδομένου ότι ένας αριθμός καταλαμβάνει χώρο 1 byte, το σύνολο των δεκαδικών ψηφίων που ανακαλύφτηκαν το 2009 καταλαμβάνει χώρο τουλάχιστον 2,343 Tera bytes και απαιτεί την χρήση σκληρού δίσκου, ή δίσκων, πολύ μεγάλης χωρητικότητας!!!!!

Το συνδικάτο των ΜΑΘΗΜΑΤΙΚΩΝ

Εν κατακλείδι..

Στατιστικά στο 97,0128% του αριθμού που ανακαλύφτηκε το 1997.

http://www.cecm.sfu.ca/~jborwein/Kanada_50b.html

Yasumasa KANADA and Daisuke TAKAHASHI (1997)

Happy the globalized new world record of pi!!!!

CC BY-NC-SA 4.0 Προοίμιο. από ΝΙΚΟΣ ΠΑΝΟΥΣΟΠΟΥΛΟΣ διατίθεται με άδεια χρήσης Creative Commons -Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή4.0.