Η “εξίσωση” ενός χρησμού
Η αρχή της ιστορίας των εξισώσεων τρίτου βαθμού βρίσκεται στην καρδιά ενός φημισμένου προβλήματος των αρχαίων ελληνικών μαθηματικών.
Το Δήλιο πρόβλημα, ή, αλλιώς, ο “διπλασιασμός” του κύβου, δηλαδή, η κατασκευή ενός κύβου με διπλάσιο όγκο από ένα δεδομένο κύβο, ήταν ένα γεωμετρικό πρόβλημα με, κάπως, ασαφή και μυστηριώδη προέλευση. Σύμφωνα με την εκδοχή που έδωσε ο μαθηματικός, φιλόσοφος και σχολιαστής των αρχαίων ελληνικών μαθηματικών Θέων ο Σμυρναίος (τέλος 1ου – αρχές 2ου αιώνα μ.Χ.), τέθηκε διά μέσου ενός χρησμού.
Το 430 π.Χ., περίπου, ο θεός Απόλλωνας διαμηνούσε στους κατοίκους της Δήλου, σύμφωνα με τον χρησμό, ότι για να απαλλαγούν από τον λοιμό, που μάστιζε την πόλη τους, θα έπρεπε να “διπλασιάσουν” τον κυβικό βωμό του στο νησί.
Οι κάτοικοι, λόγω των δυσκολιών που συνάντησαν στην προσπάθειά τους να ικανοποιήσουν το αίτημα του θεού, ζήτησαν τη βοήθεια του Πλάτωνα. Ο Πλάτωνας τούς επισήμανε ότι ο θεός ήθελε, περισσότερο από το να “διπλασιαστεί” ο βωμός του ναού του, να τους δώσει, μ’ αυτόν τον τρόπο, ένα μάθημα για την παραμέληση των Μαθηματικών και, ιδιαίτερα, για την περιφρόνηση της Γεωμετρίας.
Ωστόσο, είναι πιθανό το πρόβλημα να ήταν γνωστό νωρίτερα. Για την επίλυσή του, αρκεί, φυσικά, να κατασκευαζόταν η ακμή του ζητούμενου κύβου, δηλαδή, με σημερινό συμβολισμό, η λύση της τριτοβάθμιας εξίσωσης,
![]()
όπου ![]() παριστάνει την ακμή του δεδομένου κύβου.
παριστάνει την ακμή του δεδομένου κύβου.
Όμως, η παραπάνω αλγεβρική έκφραση του προβλήματος είναι μεταγενέστερη. Οι προσπάθειες επίλυσής του, από τους αρχαίους Έλληνες μαθηματικούς, πραγματοποιήθηκαν μέσα στο γεωμετρικό πλαίσιο της εποχής το οποίο, τελικά, εμπλούτισαν με νέες καμπύλες και ιδιοφυείς – ακόμη και τριών διαστάσεων – μηχανικές κατασκευές.
Αναζητήθηκε, επισταμένα, κατασκευή με κανόνα και διαβήτη, χωρίς, φυσικά, επιτυχία, αφού, όπως απέδειξε το 1837 ο Γάλλος μαθηματικός Pierre Wantzel, κάτι τέτοιο είναι αδύνατο.
Ο Ιπποκράτης ο Χίος (περίπου 470 – 410 π.Χ.) ανήγαγε το πρόβλημα στην εύρεση δύο μέσων αναλόγων μεταξύ του τμήματος της ακμής του δεδομένου κύβου και του διπλάσιου αυτού του τμήματος. Με σύγχρονη ορολογία, αυτό σημαίνει να βρεθούν ![]() ,
, ![]() , τέτοια, ώστε,
, τέτοια, ώστε,
![]()
Το ![]() είναι η ζητούμενη ακμή, διότι, συνδυάζοντας, κατάλληλα, τις τελευταίες ισότητες, προκύπτει ότι,
είναι η ζητούμενη ακμή, διότι, συνδυάζοντας, κατάλληλα, τις τελευταίες ισότητες, προκύπτει ότι,
![]()
Δεν είναι σίγουρο τι οδήγησε τον Ιπποκράτη σ’ αυτήν τη διαπίστωση. Μοιάζει, όμως, λογικό να υποτεθεί ότι γνώριζε το πρόβλημα “διπλασιασμού” του τετραγώνου. Διότι ο “διπλασιαμός” του τετραγώνου ισοδυναμεί με το πρόβλημα εύρεσης του μέσου αναλόγου μεταξύ του τμήματος της πλευράς του τετραγώνου και του διπλάσιου αυτού του τμήματος. Παρεμπιπτόντως, το τετράγωνο με πλευρά τη διαγώνιο ενός δεδομένου τετραγώνου έχει διπλάσιο εμβαδό από το δεδομένο τετράγωνο.
Ακολουθεί μια προσπάθεια απόδοσης του συλλογισμού του Ιπποκράτη σε μια γλώσσα περισσότερο οικεία προς εκείνη την εποχή, μια γλώσσα γεωμετρική. Βέβαια, για λόγους συντομίας στην έκφραση και μόνο, διατηρούνται ορισμένοι αλγεβρικοί συμβολισμοί. Θεωρείται, επίσης, γνωστή η γεωμετρική κατασκευή του μέσου αναλόγου δύο ευθύγραμμων τμημάτων.
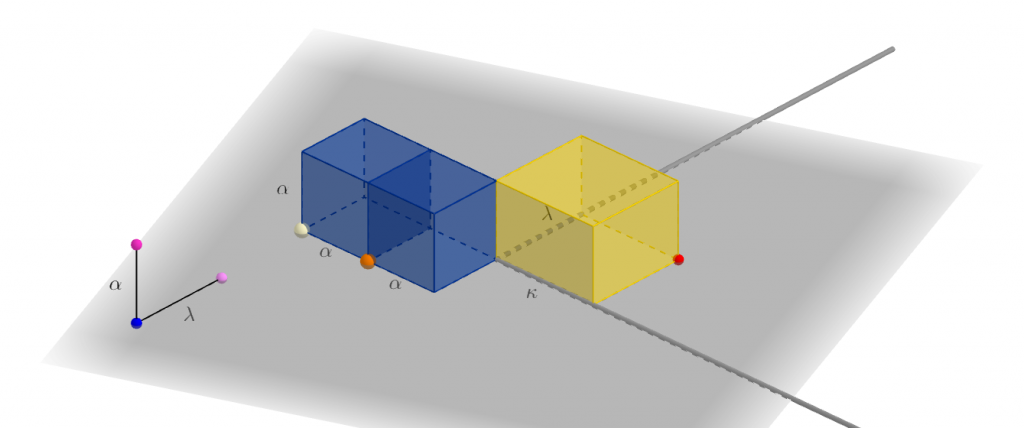
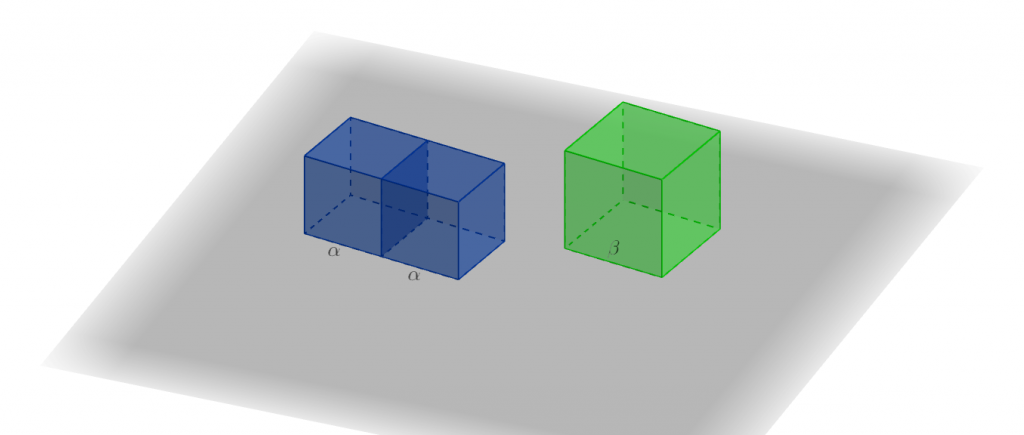
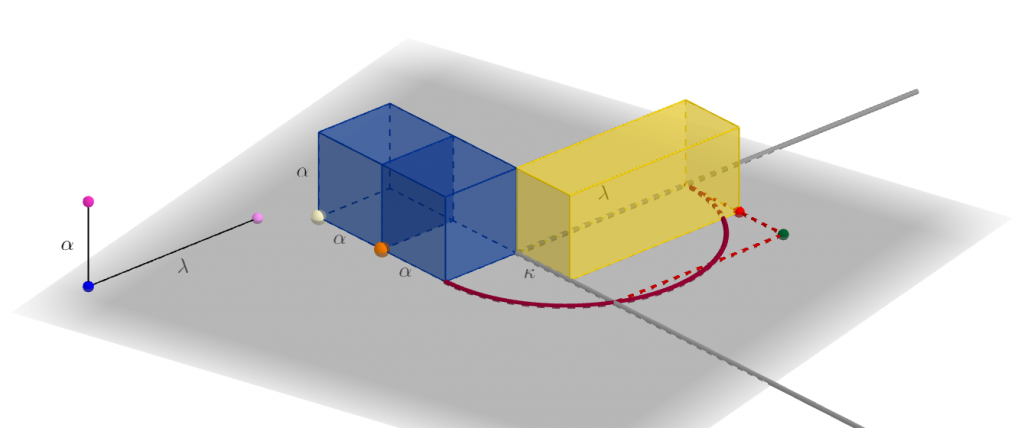
Το παραλληλεπίδο που σχηματίζουν δύο κύβοι ίσοι με τον δεδομένο κύβο, όταν τοποθετηθούν, έτσι, ώστε να ταυτίζονται δύο έδρες τους, έχει όγκο ίσο με τον όγκο κάθε παραλληλεπιπέδου το οποίο έχει εμβαδόν βάσης ![]() και ύψος
και ύψος ![]() .
.
Στο παρακάτω γραφικό,
με το οποίο μπορείτε να αλληλεπιδράσετε, παριστάνεται μια “οικογένεια” ορθογώνιων παραλληλεπιπέδων, με ύψη ![]() , όπου οι διαστάσεις των βάσεών τους
, όπου οι διαστάσεις των βάσεών τους ![]() και
και ![]() μεταβάλλονται, ώστε το γινόμενό τους να παραμένει σταθερό, ίσο με
μεταβάλλονται, ώστε το γινόμενό τους να παραμένει σταθερό, ίσο με ![]() .
.
Συνεπώς, τα τμήματα ![]() και
και ![]() είναι ανάλογα προς τα τμήματα
είναι ανάλογα προς τα τμήματα ![]() και
και ![]() . (Συνθήκη 1).
. (Συνθήκη 1).
(Βάσει αυτής της συνθήκης, άλλωστε, με χρήση όμοιων τριγώνων, κατασκευάστηκε το παραπάνω δυναμικό σχήμα.)
Επίσης, καθεμία από τις δύο διαστάσεις μπορεί να πάρει οποιαδήποτε θετική τιμή, επιλέγοντας, κατάλληλα, κάποιο “μέλος” της οικογένειας.
Κατά κάποιον τρόπο, στο “κίτρινο” παραλληλεπίπεδο, έχουν “απελευθερωθεί” το μήκος και το πλάτος του “μπλε” παραλληλεπιπέδου, με μόνη δέσμευση αυτήν που απορρέει από τη Συνθήκη 1.
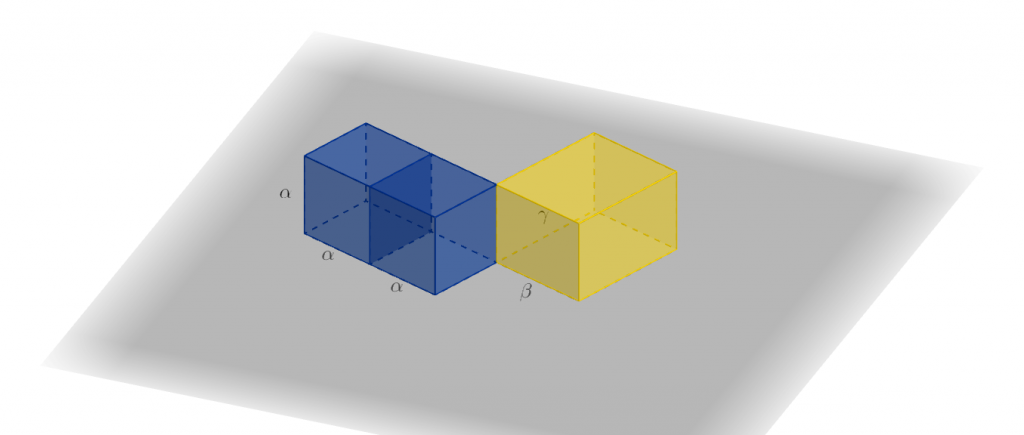
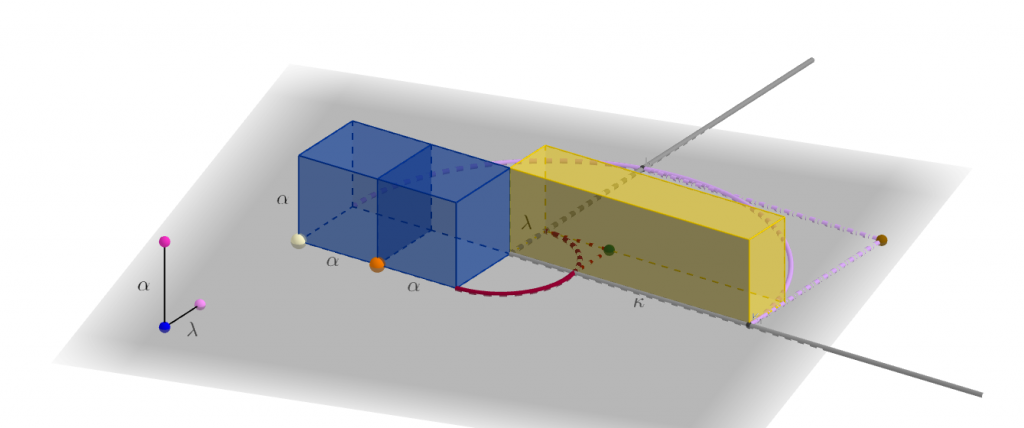
Αναλύοντας, λοιπόν, το πρόβλημα, ας υποτεθεί ότι η ζητούμενη ακμή, ![]() , κατασκευάστηκε.
, κατασκευάστηκε.
Φυσικά, ο κύβος ακμής ![]() θα έχει ίσο όγκο και με καθένα από τα μέλη της προηγούμενης οικογένειας.
θα έχει ίσο όγκο και με καθένα από τα μέλη της προηγούμενης οικογένειας.
Προφανώς, κάποιο απ’ αυτά τα παραλληλεπίπεδα έχει μήκος ![]() . Αν
. Αν ![]() συμβολίζει το πλάτος του, τότε, κάθε πλαϊνή έδρα του έχει εμβαδό όσο το τετράγωνο πλευράς
συμβολίζει το πλάτος του, τότε, κάθε πλαϊνή έδρα του έχει εμβαδό όσο το τετράγωνο πλευράς ![]() .
.
Συνεπώς το ![]() είναι μέσο ανάλογο των
είναι μέσο ανάλογο των ![]() και
και ![]() .
.
Απαιτείται, λοιπόν, το ![]() να είναι μέσο ανάλογο των
να είναι μέσο ανάλογο των ![]() και
και ![]() . (Συνθήκη 2).
. (Συνθήκη 2).
Εύκολα, αποδεικνύεται ότι το συμπέρασμα του Ιπποκράτη ισοδυναμεί με την ταυτόχρονη ισχύ των Συνθηκών 1 και 2.
Αλληλεπιδρώντας με το παρακάτω γραφικό,
μπορείτε να προσπαθήσετε να ικανοποιήσετε ταυτόχρονα τις δύο συνθήκες, συνθέτοντας τη λύση στο πρόβλημα του διπλασιασμού του κύβου.
Θα ανακαλύψετε τον έναν απ’ τους δύο τρόπους, που έδωσε ο Μέναιχμος (περίπου 380 π.Χ. – 320 π.Χ.), για την εύρεση των τιμών των ![]() και
και ![]() , χρησιμοποιώντας την τομή δύο νέων, για εκείνη την εποχή, καμπυλών: μιας παραβολής και μιας υπερβολής.
, χρησιμοποιώντας την τομή δύο νέων, για εκείνη την εποχή, καμπυλών: μιας παραβολής και μιας υπερβολής.
Ο Μέναιχμος έδωσε και δεύτερο τρόπο λύσης στο πρόβλημα, χρησιμοποιώντας, αυτή τη φορά, την τομή δύο παραβολών.
Πραγματικά, λόγω της Συνθήκης 1, τα τμήματα ![]() και
και ![]() είναι ανάλογα προς τα τμήματα
είναι ανάλογα προς τα τμήματα ![]() και
και ![]() , ενώ, λόγω της Συνθήκης 2, τα τμήματα
, ενώ, λόγω της Συνθήκης 2, τα τμήματα ![]() και
και ![]() είναι ανάλογα προς τα τμήματα
είναι ανάλογα προς τα τμήματα ![]() και
και ![]() . Επομένως, τα τμήματα
. Επομένως, τα τμήματα ![]() και
και ![]() είναι ανάλογα προς τα τμήματα
είναι ανάλογα προς τα τμήματα ![]() και
και ![]() .
.
Αυτό σημαίνει ότι το ![]() είναι μέσο ανάλογο των
είναι μέσο ανάλογο των ![]() και
και ![]() . (Συνθήκη 3.)
. (Συνθήκη 3.)
Ο δεύτερος τρόπος του Μέναιχμου συνθέτει τις Συνθήκες 2 και 3.
Άλλοι αρχαίοι Έλληνες μαθηματικοί, ανάμεσά τους ο Αρχύτας, ο Απολλώνιος, ο Διοκλής, ο Ερατοσθένης, ο Εύδοξος κι ο Νικομήδης, έδωσαν διαφορετικές λύσεις στο πρόβλημα. Όλες αυτές οι μέθοδοι οδηγούν, τροποντινά, στη γεωμετρική κατασκευή της λύσης μιας εξίσωσης τρίτου βαθμού.
Ας σημειωθεί, τέλος, ότι το πρόβλημα διερευνήθηκε και επιλύθηκε, από τους αρχαίους Έλληνες, σε μια γενικότερη μορφή, στην οποία, πάλι, αναζητούνταν δύο μέσοι ανάλογοι, όχι, όμως, μεταξύ ενός τμήματος και του διπλάσιου αυτού του τμήματος, αλλά μεταξύ δύο τμημάτων. Οι δύο μέσοι ανάλογοι παρίσταναν τις ακμές δύο κύβων, όπου ο πρώτος έχει όγκο ίσο με το ορθογώνιο παραλληλεπίπεδο, που έχει βάση τετράγωνο πλευράς όσο το πρώτο τμήμα και ύψος όσο το δεύτερο τμήμα, ενώ ο δεύτερος έχει όγκο ίσο με το ορθογώνιο παραλληλεπίπεδο, που έχει βάση τετράγωνο πλευράς όσο το δεύτερο τμήμα και ύψος όσο το πρώτο τμήμα.
Χρόνια αργότερα, ο Πέρσης φιλόσοφος, μαθηματικός, αστρονόμος και ποιητής Ομάρ Καγιάμ (1048 – 1131), θα γενικεύσει τις μεθόδους των Ελλήνων για την επίλυση διάφορων τύπων εξισώσεων τρίτου βαθμού.
Αναφορές
- Henderson D.W., Geometric Solutions of quadratic and Cubic Equations, Department of Mathematics, Cornell University.
- O’Connor J. J. and Robertson E. F., Doubling the cube, School of Mathematics and Statistics University of St Andrews, Scotland , 1999.


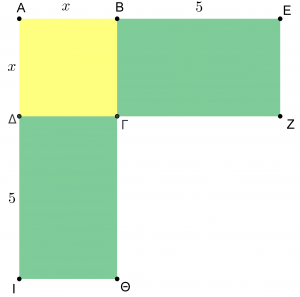
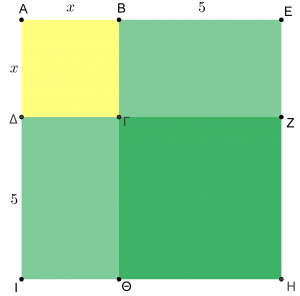





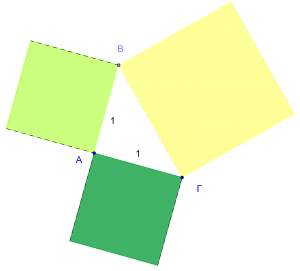 του τετραγώνου;
του τετραγώνου;