Στα Μαθηματικά, μια ισότητα που περιέχει μεταβλητές και ισχύει για όλες τις τιμές των μεταβλητών της λέγεται ταυτότητα.
Ορισμένες αξιοσημείωτες ταυτότητες αναδύονται μέσα από γεωμετρικά σχήματα.
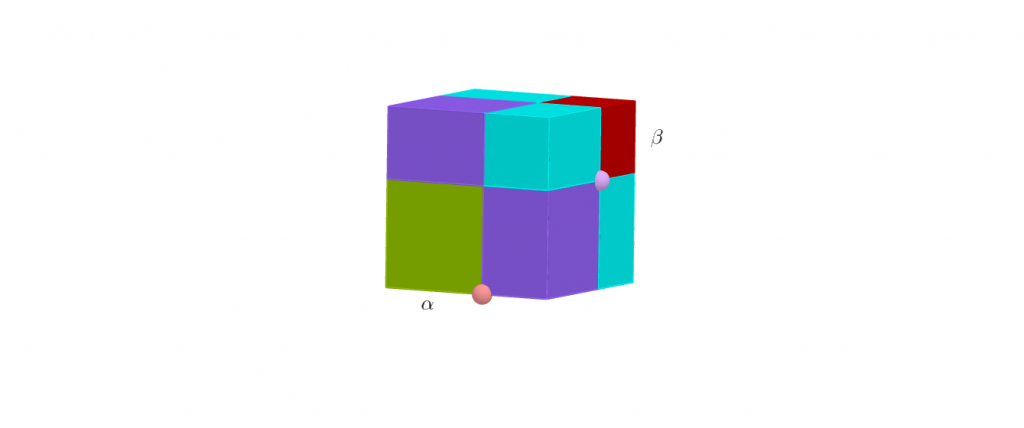
Αλληλεπιδρώντας με το ακόλουθο γραφικό,
μπορείτε να επεξεργαστείτε τις ακόλουθες δραστηριότητες και, γιατί όχι, να αναζητήσετε τη δική σας ταυτότητα …
Τετράγωνο «αθροίσματος»
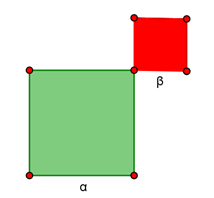
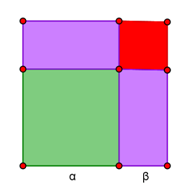
Δραστηριότητα 1 Να τοποθετήσετε δύο τετράγωνα με τέτοιον τρόπο, έτσι, ώστε να σκιαγραφηθεί το μικρότερο τετράγωνο το οποίο «περιέχει» το «άθροισμα» τους.
Τι άλλο «περιέχει» το συγκεκριμένο τετράγωνο εκτός από το «άθροισμα» των αρχικών τετραγώνων;
Μπορείτε να εκφράσετε αλγεβρικά το συμπέρασμά σας;
Τετράγωνο «διαφοράς»
Δραστηριότητα 2 Να τοποθετήσετε δύο τετράγωνα με τέτοιον τρόπο, έτσι, ώστε να σκιαγραφηθεί το μεγαλύτερο τετράγωνο το οποίο «περιέχεται» στη «διαφορά» τους.
Τι άλλο «περιέχει» η «διαφορά» των αρχικών τετραγώνων εκτός από το συγκεκριμένο τετράγωνο;
Μπορείτε να εκφράσετε αλγεβρικά το συμπέρασμά σας;
«Διαφορά» τετραγώνων
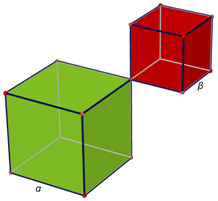
Δραστηριότητα 3 Να τοποθετήσετε δύο τετράγωνα με τέτοιον τρόπο, έτσι, ώστε να σκιαγραφηθεί ένα σχήμα που παριστάνει τη «διαφορά» τους, το οποίο να μπορεί να μετασχηματιστεί σε ένα σχήμα προσδιορίσιμου εμβαδού.
Μπορείτε να εκφράσετε αλγεβρικά το συμπέρασμά σας;