Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής, μπορείτε να εξασκηθείτε στη χάραξη των γραφικών παραστάσεων ορισμένων βασικών συναρτήσεων.
Συγγραφέας: dkonas | Κατηγορία Για την Γ΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Γ΄ Λυκείου, Μαθηματικά και Στοιχεία Στατιστικής Γ΄ Λυκείου | , στις 27-09-2014
Συγγραφέας: dkonas | Κατηγορία Για την Γ΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Γ΄ Λυκείου | , στις 20-10-2012
Το “χρέος” των μιγαδικών …
“[…] Έχετε υπάρξει βετεράνοι των δημιουργικών βασάνων. Συνεχίστε να εργάζεστε με την πίστη ότι τα αναίτια βάσανα είναι λυτρωτικά. […]”
Μάρτιν Λούθερ Κινγκ, “Έχω ένα όνειρο”
Το αδιέξοδο, στο οποίο οδηγήθηκε η μέθοδος των “Καρντάνο – Ταρτάλια”, για το πρόβλημα της επίλυσης των τριτοβάθμιων εξισώσεων,
(1) ![]()
στην περίπτωση όπου,
![]()
αποτέλεσε την αφορμή για την υλοποίηση της ιδέας της διεύρυνσης του συνόλου ![]() των πραγματικών στο σύνολο
των πραγματικών στο σύνολο ![]() των μιγαδικών.
των μιγαδικών.
Πλέον, με τη συγκρότηση του ![]() , μπορεί να αναζητηθεί, για την (1), λύση της μορφής,
, μπορεί να αναζητηθεί, για την (1), λύση της μορφής, ![]() , όπου,
, όπου, ![]() , τέτοια, ώστε,
, τέτοια, ώστε,
![]()
ή, ισοδύναμα, τέτοια ώστε,

Είναι αξιοσημείωτο ότι, στο πλαίσιο της αναζήτησης λύσης για το (Σ), ανακύπτουν βασικές έννοιες για το σύνολο ![]() , όπως η έννοια του συζυγούς, του μέτρου και της τριγωνομετρικής μορφής ενός μιγαδικού αριθμού, καθώς και βασικά συμπεράσματα που τις διέπουν, με κυριότερο το Θεώρημα De Moivre.
, όπως η έννοια του συζυγούς, του μέτρου και της τριγωνομετρικής μορφής ενός μιγαδικού αριθμού, καθώς και βασικά συμπεράσματα που τις διέπουν, με κυριότερο το Θεώρημα De Moivre.
Παρατήρηση 1 Στο σύνολο ![]() , μια εξίσωση της μορφής,
, μια εξίσωση της μορφής, ![]() με
με ![]() , ισοδύναμα, γράφεται,
, ισοδύναμα, γράφεται,
![]()
επομένως, έχει ακριβώς δύο λύσεις τις ![]() και
και ![]() .
.
Με βάση την προηγούμενη παρατήρηση, από τη δεύτερη εξίσωση του (Σ), έπεται ότι,
![]()
Οπότε, μια δυνατή επιλογή για το ![]() , μπορεί να προκύψει από την ισότητα,
, μπορεί να προκύψει από την ισότητα,
(2) ![]()
ενώ, η αντίστοιχη επιλογή για το ![]() πρέπει να πληροί,
πρέπει να πληροί,
(3) ![]()
Αν υποτεθεί ότι υπάρχει, για τη (2), λύση της μορφής,
![]()
εύλογα, διερωτάται κανείς, αν, όπως στην περίπτωση όπου ![]() , ο αντίθετος του συζυγή του
, ο αντίθετος του συζυγή του ![]() ,
,
![]()
είναι λύση της (3).
Η απάντηση είναι καταφατική και απορρέει από την ιδιότητα,
![]()
που, εύκολα, αποδεικνύεται ότι ισχύει για οποιουσδήποτε ![]() .
.
Πράγματι,
![]()
Επειδή,
![]()
αρκεί, λόγω του (Σ), να βρεθούν ![]() τέτοια, ώστε,
τέτοια, ώστε,
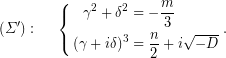
Παρατήρηση 2 Αφού ![]() , προφανώς
, προφανώς ![]() .
.
Η πρώτη εξίσωση του (Σ΄), γράφεται,
![Rendered by QuickLaTeX.com \[ \Bigg(\dfrac{\gamma}{\sqrt{-\dfrac{m}{3}}}\Bigg)^2+\Bigg(\dfrac{\delta}{\sqrt{-\dfrac{m}{3}}}\Bigg)^2=1. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-d4860922ea5809448b8c5e333da88d66_l3.png?x32006)
Θέτουμε,
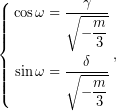
άρα,

(Με ![]() συμβολίζονται το συνημίτονο και το ημίτονο αντίστοιχα.)
συμβολίζονται το συνημίτονο και το ημίτονο αντίστοιχα.)
Αντικαθιστώντας στη δεύτερη εξίσωση του (Σ΄),
![]()
επομένως,
![Rendered by QuickLaTeX.com \[ \left(\cos\omega+i\sin\omega\right)^3=\dfrac{\dfrac{n}{2}}{\sqrt{-\dfrac{m}{3}}^{3}}+i\dfrac{\sqrt{-D}}{\sqrt{-\dfrac{m}{3}}^{3}}. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-6f7a69efa6e8d566f77108122faf0d88_l3.png?x32006)
Με τη βοήθεια γνωστών τριγωνομετρικών ταυτοτήτων,

Συνεπώς,
![Rendered by QuickLaTeX.com \[ \cos(3\omega)+i\sin(3\omega)=\dfrac{\dfrac{n}{2}}{\sqrt{-\dfrac{m}{3}}^{3}}+i\dfrac{\sqrt{-D}}{\sqrt{-\dfrac{m}{3}}^{3}}. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-a8e7dc3d2bfaf1750f93e876e3616a67_l3.png?x32006)
Άρα, αρκεί να βρεθεί γωνία ![]() τέτοια, ώστε,
τέτοια, ώστε,

Όμως,
![Rendered by QuickLaTeX.com \[ \Bigg(\dfrac{\dfrac{n}{2}}{\sqrt{-\dfrac{m}{3}}^{3}}\Bigg)^2+\Bigg(\dfrac{\sqrt{-D}}{\sqrt{-\dfrac{m}{3}}^{3}}\Bigg)^2=\dfrac{\Big(\dfrac{n}{2}\Big)^2-D}{-\Big(\dfrac{m}{3}\Big)^3}=1, \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-60cb133984cd1646b29f34c0b0345ad2_l3.png?x32006)
δηλαδή, υπάρχουν άπειρες λύσεις για το παραπάνω σύστημα.
Αν ![]() είναι μια τέτοια λύση, τότε,
είναι μια τέτοια λύση, τότε, ![]() είναι λύση του (Σ΄), όπου,
είναι λύση του (Σ΄), όπου,

οπότε, ![]() είναι λύση του (Σ), όπου,
είναι λύση του (Σ), όπου,

Άρα,
![]()
είναι μία πραγματική λύση της (1).
Με τη βοήθεια αυτής της λύσης, η (1) μετασχηματίζεται ως εξής,
![]()
![]()
![]()
![]()
![]()
![]()
συνεπώς, γράφεται, τελικά,
(4) ![]()
Το τριώνυμο,
![]()
έχει διακρίνουσα,
![]()
Τελικά, η (1), όταν ![]() έχει τρεις πραγματικές λύσεις που δίνονται από τους τύπους,
έχει τρεις πραγματικές λύσεις που δίνονται από τους τύπους,

Παράδειγμα 1 Για την εξίσωση, ![]() , έχουμε,
, έχουμε, ![]() , συνεπώς,
, συνεπώς,
![]()
Αναζητείται ![]() , τέτοιο, ώστε,
, τέτοιο, ώστε,

οπότε, μπορεί να επιλεγεί ως ![]() το
το ![]() .
.
Άρα, η εξίσωση έχει τρεις πραγματικές λύσεις,

Συγγραφέας: dkonas | Κατηγορία Για την Γ΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Γ΄ Λυκείου | , στις 30-09-2012
“Φανταστικές” … επινοήσεις
Η πρώτη σημαντική πρόοδος στην αλγεβρική επίλυση των τριτοβάθμιων εξισώσεων σημειώνεται στην Ιταλία. Γύρω στο 1515, ο καθηγητής Μαθηματικών Σκιπιόνε νταλ Φέρο (1465-1526), κάτοχος της Έδρας Αριθμητικής και Γεωμετρίας στο Πανεπιστήμιο της Μπολόνια, ανακάλυψε τον τύπο επίλυσης των τριτοβάθμιων εξισώσεων της μορφής,
(1) ![]()
Φυσικά, το γενικό πρόβλημα ανάγεται στην προηγούμενη περίπτωση, μιας και κάθε τριτοβάθμια εξίσωση μπορεί να μετασχηματιστεί όπως παραπάνω με τη μέθοδο “συμπλήρωσης κύβου”.
O νταλ Φέρο κράτησε μυστική την ανακάλυψή του, ωσότου, λίγο πριν τον θάνατό του, την αποκαλύψει στον μαθητή του Αντόνιο Φιόρ.
Έπειτα από δέκα χρόνια, περίπου, ένας προικισμένος μαθηματικός, ο Νικολό Φοντάνα (1499 – 1557), επονομαζόμενος Ταρτάλια, δημοσιοποίησε τον τρόπο επίλυσης τριτοβάθμιων εξισώσεων της μορφής,
![]()
(Ο Φοντάνα έμεινε στην Ιστορία ως “Ταρτάλια”, που σημαίνει τραυλός, εξαιτίας ενός προβλήματος στην άρθρωσή του, έπειτα από ένα σοβαρό παιδικό τραύμα που λίγο έλειψε να του κοστίσει τη ζωή.)
Μετά απ’ αυτήν την εξέλιξη, ο Φιόρ προκάλεσε τον Ταρτάλια σε δημόσιο διαγωνισμό, όπου καθένας τους, εντός διαστήματος 40 ή 50 ημερών, έπρεπε να επιλύσει 30 προβλήματα κυβικών εξισώσεων. Νικητής θα ανακηρυσσόταν εκείνος που θα έλυνε τα περισσότερα. Όμως, οχτώ ημέρες προτού ξεκινήσει ο διαγωνισμός, ο Ταρτάλια είχε καταφέρει να ανανακαλύψει, ανεξάρτητα, τον γενικό τρόπο επίλυσης κυβικών εξισώσεων της μορφής (1). Όλα τα προβλήματα που τέθηκαν από τον Φιόρ ήταν, τροποντινά, αυτής της μορφής, με αποτέλεσμα να λυθούν από τον Ταρτάλια μέσα σε δύο ώρες.
Αργότερα, ο ιδιοφυής μαθηματικός Τζερόλαμο Καρντάνο (1501 – 1576) προσέγγισε τον Ταρτάλια, καταφέρνοντας, με αθέμιτα μέσα, να του αποσπάσει τις ανακαλύψεις του. Στο σπουδαίο έργο του “Μεγάλη τέχνη”, μια πραγματεία στην Άλγεβρα που δημοσιεύτηκε το 1545, παρουσιάζεται ο τύπος με τη βοήθεια του οποίου υπολογίζονται οι ρίζες των κυβικών εξισώσεων.
Ακριβέστερα, ο τύπος με τη βοήθεια του οποίου, αργότερα, θα μπορούσαν να υπολογιστούν οι ρίζες των κυβικών εξισώσεων. Διότι, τουλάχιστον, έτσι όπως αρχικά χρησιμοποιούταν, ήταν δυνατόν να υπολογιστούν μόνο οι ρίζες εξισώσεων όπου οι συντελεστές τους ικανοποιούσαν μια συγκεκριμένη συνθήκη. Ο ίδιος ο Καρντάνο είχε διερευνήσει γενικότερα το πρόβλημα έχοντας επικοινωνήσει, σχετικά, με τον Ταρτάλια. Παρότι έκανε βήματα προς τη σωστή κατεύθυνση, εντούτοις, ελλείψει απτών αποτελεσμάτων, χαρακτήρισε τη μέθοδό του “περισσότερο δεξιοτεχνική, παρά χρήσιμη”. Έτσι, αναγκάστηκε να παραδεχτεί αυτήν την “αδυναμία”, παραπέμποντας, μάλιστα, στις γεωμετρικές τεχνικές του παρελθόντος για μια πληρέστερη αντιμετώπιση του όλου προβλήματος.
Ο Ραφαήλ Μπομπέλι (1526 – 1572), ανίχνευσε με μεγαλύτερη “νηφαλιότητα” και “χωρίς αναστολές” τα “σκοτεινά” σημεία στο έργο του Καρντάνο. Τη χρονιά του θανάτου του, εκδίδεται το βιβλίο του “Άλγεβρα”, στο οποίο ο Μπομπέλι “αποδέχεται” ποσότητες, εκτός του μαθηματικού πλαισίου της εποχής, διευρύνοντας το πεδίο εφαρμογής των τύπων επίλυσης των κυβικών εξισώσεων.
Μέσα από τις διάφορες φάσεις της, με σύγχρονο συμβολισμό και λίγη … “φαντασία”, η ιστορία είχε ως εξής.
Η ταυτότητα,
![]()
η οποία γράφεται,
![]()
υποδεικνύει, για την (1), αναζήτηση λύσης της μορφής, ![]() , με
, με ![]() , όπου,
, όπου,
![]()
Διαδοχικά,

οπότε, προκύπτει το σύστημα,

Η δεύτερη εξίσωση του (Σ) είναι δεύτερου βαθμού ως προς ![]() και έχει διακρίνουσα,
και έχει διακρίνουσα,

Έστω,
![]()
Περίπτωση Ι)
![]()
Από τη δεύτερη εξίσωση του (Σ), έπεται ότι,
![]()
Οπότε, μια δυνατή επιλογή για το ![]() είναι,
είναι,
![]()
Η αντίστοιχη επιλογή για το ![]() είναι,
είναι,
![]()
Επομένως, μια ρίζα της εξίσωσης είναι, ![]() , δηλαδή,
, δηλαδή,
(2) ![]()
Με τη βοήθεια αυτής της λύσης, η (1) μετασχηματίζεται ως εξής,
![]()
![]()
![]()
![]()
![]()
![]()
συνεπώς, γράφεται, τελικά,
(3) ![]()
Το τριώνυμο,
![]()
έχει διακρίνουσα,
![]()
η οποία έχει αρνητικό πρόσημο διότι,
![]()
Επομένως, η ![]() είναι η μοναδική πραγματική λύση της (1).
είναι η μοναδική πραγματική λύση της (1).
Έπειτα, κάτι φαινομενικά περιττό:
Θα εκφραστούν τα ![]() με τη βοήθεια της
με τη βοήθεια της ![]() .
.
Για το σκοπό αυτό, παρατηρούμε ότι,

που σημαίνει ότι τα ![]() είναι οι ρίζες της εξίσωσης,
είναι οι ρίζες της εξίσωσης,
![]()
Άρα,
(4) 
Παρατήρηση 1 Από τις εκφράσεις (4), έπεται ότι το ![]() είναι ο αντίθετος του συζυγή του
είναι ο αντίθετος του συζυγή του ![]() .
.
Στα επόμενα, θα φανεί η σημασία της τελευταίας παρατήρησης.
Παράδειγμα 1 Για την εξίσωση, ![]() , είναι,
, είναι, ![]() , συνεπώς,
, συνεπώς,
![]()
οπότε, έχει μοναδική πραγματική λύση,
![]()
Από την άλλη μεριά, βάσει της λύσης ![]() , χρησιμοποιώντας τους τύπους (4),
, χρησιμοποιώντας τους τύπους (4),

Οι παραπάνω εναλλακτικές εκφράσεις για τα ![]() , στο προηγούμενο παράδειγμα, δεν προσθέτουν, φυσικά, τίποτα καινούριο στην επίλυση της συγκεκριμένης εξίσωσης. Ωστόσο, με την ένταξή τους, μπορεί κανείς να είναι περισσότερο υποψιασμένος για τα όσα ακολουθούν.
, στο προηγούμενο παράδειγμα, δεν προσθέτουν, φυσικά, τίποτα καινούριο στην επίλυση της συγκεκριμένης εξίσωσης. Ωστόσο, με την ένταξή τους, μπορεί κανείς να είναι περισσότερο υποψιασμένος για τα όσα ακολουθούν.
Περίπτωση ΙΙ)
![]()
Για την ώρα, η ειδική περίπτωση της εξίσωσης,
(5) ![]()
για την οποία είναι, ![]() , οπότε,
, οπότε,
![]()
Σύμφωνα με την ανάλυση που έγινε στην Περίπτωση Ι, γίνεται φανερό ότι δεν υπάρχει λύση ![]() της μορφής
της μορφής ![]() με
με ![]() , τέτοια, ώστε,
, τέτοια, ώστε,
![]()
Από την άλλη μεριά, η εξίσωση έχει προφανή λύση τη ![]() . Έτσι, παραγοντοποιώντας, γράφεται, ισοδύναμα,
. Έτσι, παραγοντοποιώντας, γράφεται, ισοδύναμα,
(6) ![]()
Συνεπώς, οι ρίζες της είναι,
![]()
Επομένως, η (6) έχει τρεις πραγματικές ρίζες.
Επιπλέον, σ’ αυτήν την περίπτωση, οι τύποι (4) δεν ισχύουν, ωστόσο, αν τα “εξαγόμενά τους”,

για τη λύση ![]() , μπορούσαν να ενσωματωθούν στην “οικογένεια” των αριθμών, εμπλουτίζοντάς την, με τέτοιο τρόπο, έτσι, ώστε, να “υπακούν” στους “νόμους” των πράξεων, τότε η (6) θα ήταν, πάλι, της μορφής (3). Πράγματι,
, μπορούσαν να ενσωματωθούν στην “οικογένεια” των αριθμών, εμπλουτίζοντάς την, με τέτοιο τρόπο, έτσι, ώστε, να “υπακούν” στους “νόμους” των πράξεων, τότε η (6) θα ήταν, πάλι, της μορφής (3). Πράγματι,

Βέβαια, έστω και μ’ αυτήν την υπέρβαση, παραμένει ανοικτό το πρόβλημα εύρεσης των ![]() μιας και υπολογίστηκαν με τη βοήθεια της λύσης
μιας και υπολογίστηκαν με τη βοήθεια της λύσης ![]() της (5). Φυσικά, δε μπορεί να θεωρείται γνωστή, εκ των προτέρων, μια λύση για την τριτοβάθμια εξίσωση που επιλύεται.
της (5). Φυσικά, δε μπορεί να θεωρείται γνωστή, εκ των προτέρων, μια λύση για την τριτοβάθμια εξίσωση που επιλύεται.
Αψηφώντας, για δεύτερη φορά, βασική ιδιότητα της διάταξης των πραγματικών αριθμών, επιστρατεύεται ο τύπος (2), με την προσδοκία άμεσου υπολογισμού ρίζας για την εξίσωση (5). Έτσι,
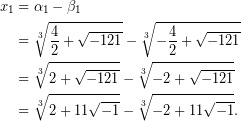
Τώρα, εφαρμόζοντας τις ιδιότητες των πράξεων, όπως στην περίπτωση των πραγματικών αριθμών, έπεται ότι,
![]()
που σημαίνει ότι,
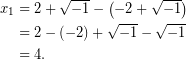
Ίσως ο υπολογισμός της ![]() να είναι, πάλι, έμμεσος, όμως, αναδεικνύεται, ξανά, το ενδεχόμενο αξιοποίησης αυτών των “φανταστικών” εκφράσεων.
να είναι, πάλι, έμμεσος, όμως, αναδεικνύεται, ξανά, το ενδεχόμενο αξιοποίησης αυτών των “φανταστικών” εκφράσεων.
Για άλλη μια φορά οι Μαθηματικοί βρέθηκαν μπροστά σ’ ένα δίλλημα. Να αποδεχτούν, κατ’ αρχήν, αυτές τις εκφράσεις, από τη στιγμή που διαφαινόταν η συνεισφορά τους στο γενικό πρόβλημα της επίλυσης της τριτοβάθμιας εξίσωσης, ή να τις απορρίψουν διότι, μέχρι τότε, στερούνταν νοήματος και, στη συνέχεια, να στραφούν σε άλλες στρατηγικές για την επίλυσή του.
Επέλεξαν αυτό που ίσως, αρχικά, έμοιαζε αδιανόητο. Η πρόκληση ήταν σίγουρα σπουδαία μα το εγχείρημα καθόλου εύκολο. Έπρεπε να θεμελιωθεί ένα υπερσύνολο των πραγματικών αριθμών το οποίο να έχει ένα στοιχείο, έστω ![]() , επιφορτισμένο να αναλάβει το ρόλο που είχε η έκφραση
, επιφορτισμένο να αναλάβει το ρόλο που είχε η έκφραση ![]() παραπάνω. Επιπλέον, να έχει τις ίδιες πράξεις με το
παραπάνω. Επιπλέον, να έχει τις ίδιες πράξεις με το ![]() και τις ίδιες ιδιότητες των πράξεων. Τα στοιχεία του, ως αποτέλεσμα των “προσμίξεών” του με τους πραγματικούς αριθμούς, έπρεπε να έχουν τη μορφή,
και τις ίδιες ιδιότητες των πράξεων. Τα στοιχεία του, ως αποτέλεσμα των “προσμίξεών” του με τους πραγματικούς αριθμούς, έπρεπε να έχουν τη μορφή,
![]()
όπου ![]() .
.
Άραγε, οι αριθμοί, εκτός από το να «αριθμούν», θα μπορούσαν, απλά, να υπόκεινται στις ιδιότητες που απορρέουν από τις αριθμητικές πράξεις;
Όταν ο αρχικός σκεπτικισμός ξεπεράστηκε, δίνοντας τη θέση του σε μια κριτική αναθεώρηση των ορισμών των διάφορων συνόλων των αριθμών, άρχισε να συγκροτείται το σύνολο ![]() των μιγαδικών. Προτεραιότητα δεν αποτέλεσε τόσο η φυσική ερμηνεία των στοιχείων του, όπως αυτά περιγράφηκαν παραπάνω, όσο η συνεπής μεταφορά, κατά τη δόμηση του νέου συνόλου, των πράξεων των πραγματικών και η ταυτόχρονη απελευθέρωση από τα δεσμά που επέβαλλε η διάταξη.
των μιγαδικών. Προτεραιότητα δεν αποτέλεσε τόσο η φυσική ερμηνεία των στοιχείων του, όπως αυτά περιγράφηκαν παραπάνω, όσο η συνεπής μεταφορά, κατά τη δόμηση του νέου συνόλου, των πράξεων των πραγματικών και η ταυτόχρονη απελευθέρωση από τα δεσμά που επέβαλλε η διάταξη.
Αναφορές
- Eves H., Great moments in Mathematics Before 1650, Mathematical Association Of America, 1983.
- Henderson D.W., Geometric Solutions of quadratic and Cubic Equations, Department of Mathematics, Cornell University.
- O’Connor J. J. and Robertson E. F., Quadratic, Cubic and quartic equations, School of Mathematics and Statistics University of St Andrews, Scotland , 1996.