e-daskalos
e-sos
Geogebra Math Apps
mathematica.gr/
math_a_magic_path
Αρωγή Παιδείας
Άσκηση
Ασκησόπολις
ΓΕ.Λ ΑΡΙΔΑΙΑΣ
ΓΕΛ Εξαπλατάνου
ΔΔΕ Πέλλας
Ε.Μ.Ε (Ελληνική Μαθ. Εταιρεία)
Ε.Μ.Ε -Κεντρικής Μακεδονίας
Ζανταρίδης-Τηλέγραφος
Μα8ηματ1κέ5 Σημ3ιώσei5 (Lisari)
Μαθη…μαγικά
Μαθηματικά & Λογοτεχνία
Ο Άγνωστος Χ
Ο Μαθηματικός
Τμήμα Μαθηματικών – Α.Π.Θ
Υπουργείο Παιδείας & Θρησκευμάτων
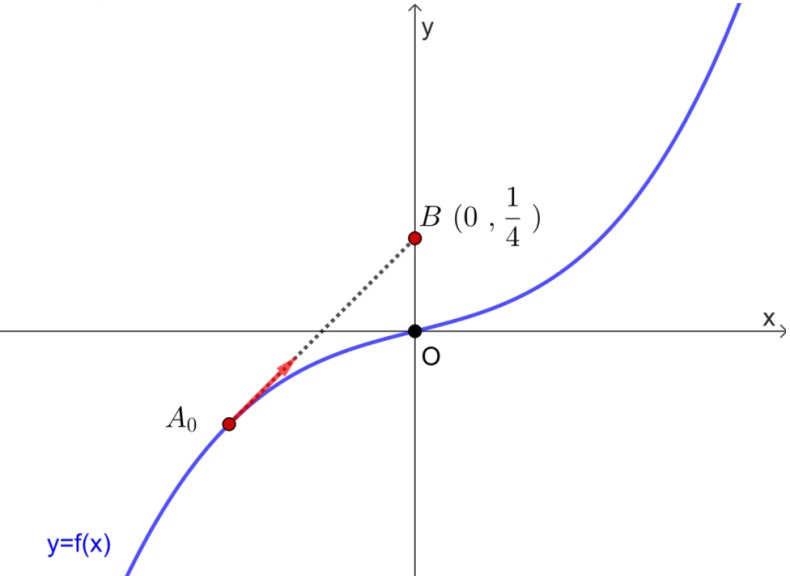
Στο διπλανό σχήμα , έχουμε δυο πασσάλους με ύψη α=10 και β=6 μέτρων αντίστοιχα, οι οποίοι συνδέονται με δυο σχοινιά τα ΒΓ και ΔΑ.
ι ) Αν η μεταξύ τους απόσταση ΑΓ, είναι ίση με 10 μέτρα , όπως στο διπλανό σχήμα, σε ποιο ύψος απ το έδαφος ΑΓ βρίσκεται η τομή των σχοινιών; Αλλιώς υπολογίστε το υ.
ιι ) Αν η μεταξύ τους απόσταση ΑΓ, είναι ίση με 16 μέτρα, σε ποιο ύψος απ το έδαφος βρίσκεται τώρα η τομή των δυο σχοινιών ;
ιιι ) Εξηγήστε, γιατί το μήκος ΕΚ (δηλαδή το υ) είναι ανεξάρτητο της απόστασης των πασσάλων , δηλαδή του ΑΓ.
ΠΗΓΗ : Οδός Μαθηματικής Σκέψης , Γ.Θωμαϊδης – Γ. Ρίζος , Εκδόσεις Μαυρίδη , Θεσσαλόνικη 2017.
Υπόδειξη για το ι) και το ιι)
Τα τρίγωνα ΑΒΓ , ΕΚΓ είναι όμοια και τα τρίγωνα ΑΕΚ , ΑΔΓ είναι όμοια. Είναι ορθογώνια και με μια οξεία γωνία κοινή. Θεωρήστε ΚΓ = χ και ΑΚ = 10-χ , τότε απ την 1η “ομοιότητα” προκύπτει υ=χ και απ την 2η “ομοιότητα” ότι υ=3.75 μ
Για το ιι) ομοίως με αλλαγή στο ΑΚ που είναι 16-χ. Και πάλι η λύση είναι υ= 3.75 μ.
Για το ιιι)
Έστω α το ύψος του ενός πάσσαλου , β το ύψος του άλλου και ρ η μεταξύ τους απόσταση.
απ τις παραπάνω ομοιότητες προκύπτουν οι σχέσεις :
υ/α = (ρ-χ)/ρ (Α)
υ/β = χ/ρ (Β)
Η (Α) μέσω της (Β) γίνεται : υ/α = 1 – υ/β
Τελικά, αποδεικνύεται ό,τι το υ είναι ανεξάρτητο της απόστασης των δυο πασσάλων και εξαρτάται απ τα ύψη α, β των πασσάλων και ισχύει: υ = αβ / (α+β) .
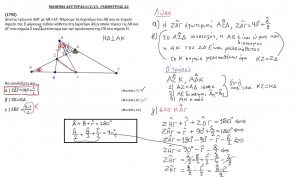
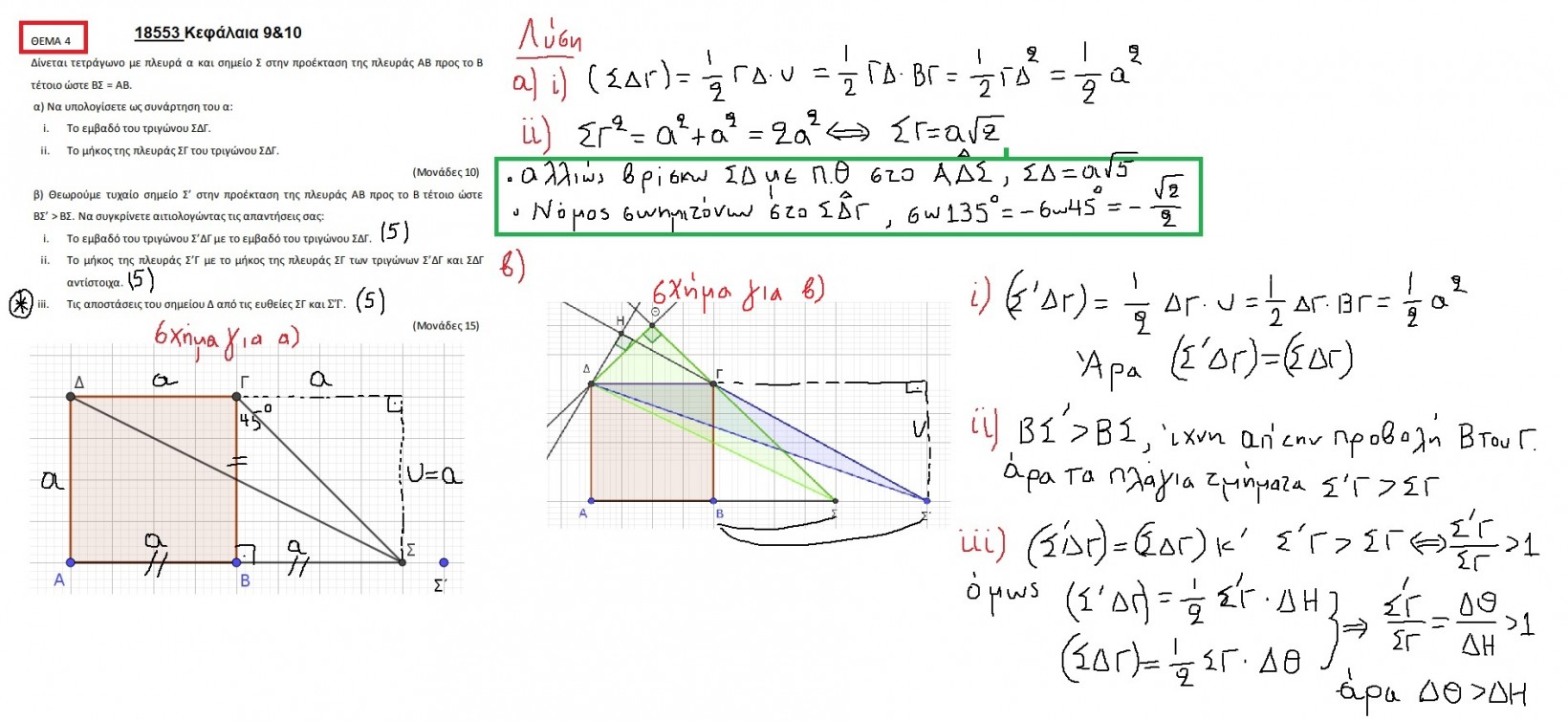
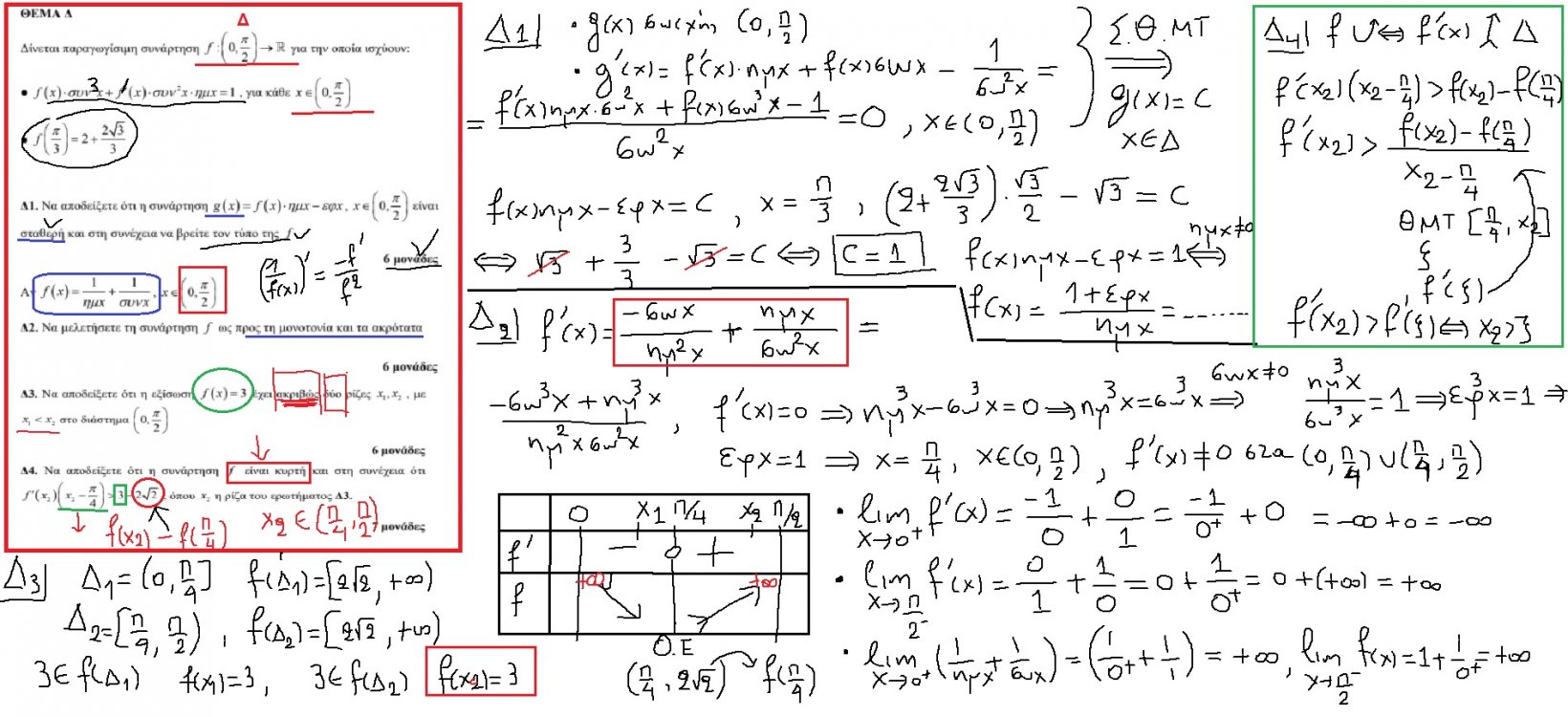
(A)Βάσει των δεδομένων της εκφώνησης έχουμε:
ΕΚ = υ, ΑΓ = 10, ΑΚ = α, και ΓΚ = (10-α)
(i)Από την ομοιότητα των ορθογωνίων τριγώνων (ΑΓΔ) και (ΑΕΚ) έχουμε::
ΑΚ/ΑΓ=ΕΚ/ΓΔ —-> α/10=υ/6 —-> 6α=10υ —-> υ=6α/10 —-> υ=0,6α (1)
(ii)Από την ομοιότητα των ορθογωνίων τριγώνων (ΑΒΓ) και (ΕΚΓ) έχουμε:
ΚΓ/ΑΓ=ΕΚ/ΑΒ —-> (10-α)/10=υ/10 —-> 10*(10-α)=10υ —-> υ=10*(10-α)/10 —->
υ=(10-α) (2)
Επειδή τα τρίγωνα είναι όμοια τα ύψη είναι ίσα, άρα έχουμε:
0,6α= 10-α —-> 0,6α+α=10 —-> α*(0,6+1)=10 —-> 1,6α=10 —> α=10/1,6 —> α=6,25μ.(3)
Αντικαθιστούμε τη (3) στη (2) κι’ έχουμε:
υ=(10-α) —-> υ=10-6,25 —-> υ=3,75μ.(4)
(B)Βάσει των δεδομένων της εκφώνησης έχουμε:
ΕΚ = υ, ΑΓ = 16, ΑΚ = α, και ΓΚ = (16-α)
(i)Από την ομοιότητα των ορθογωνίων τριγώνων (ΑΓΔ) και (ΑΕΚ) έχουμε::
ΑΚ/ΑΓ=ΕΚ/ΓΔ —-> α/16=υ/6 —-> 6α=16υ —-> υ=6α/16
Διαιρούμε το κλάσμα δια του δύο κι’ έχουμε:
υ=6α/16 —-> υ=3α/8 (1)
(ii)Από την ομοιότητα των ορθογωνίων τριγώνων (ΑΒΓ) και (ΕΚΓ) έχουμε:
ΚΓ/ΑΓ=ΕΚ/ΑΒ —-> (16-α)/16=υ/10 —-> 10*(16-α)=16υ —-> υ=10*(16-α)/16
Διαιρούμε το κλάσμα δια του δύο κι’ έχουμε:
υ=10*(16-α)/16 —-> υ=5*(16-α)/8 —-> υ=(80-5α)/8 (2)
Επειδή τα τρίγωνα είναι όμοια τα ύψη είναι ίσα, άρα έχουμε:
3α/8=(80-5α)/8 –> 3α=80-5α –>3α+5α=80 –> 8α=80 —–> α=80/8 —-> α=10 (3)
Αντικαθιστούμε τη (3) στη (2) κι’ έχουμε:
υ=(80-5α)/8 —–> υ=[80-(5*10)]/8 —–> υ=(80-50)/8 —–> υ=30/8 —–> υ=3,75μ (4)
Συμπέρασμα:
Το ύψος, όπου διασταυρώνονται τα σχοινιά, παραμένει πάντα σταθερό, ανεξάρτητα από την απόσταση των πασσάλων.
Πράγματι βάσει του κατωτέρω σκεπτικού συνάγουμε ότι το ύψος όπου διασταυρώνονται τα σχοινιά παραμένει σταθερό.
Έστω ΕΚ = υ, ΑΚ = α, και ΚΓ = β
(i)Από την ομοιότητα των ορθογωνίων τριγώνων (ΑΓΔ) και (ΑΕΚ) έχουμε::
ΑΚ/ΑΓ=ΕΚ/ΓΔ —-> α/(α+β)=υ/6 —-> 6α=υ*(α+β) —-> υ=6α/(α+β) (1)
(ii)Από την ομοιότητα των ορθογωνίων τριγώνων (ΑΒΓ) και (ΕΚΓ) έχουμε:
ΚΓ/ΑΓ=ΕΚ/ΑΒ —-> β/(α+β)=υ/10 —-> 10β=υ*(α+β) —-> υ=10β/(α+β) (2)
Επειδή τα τρίγωνα είναι όμοια τα ύψη είναι ίσα, άρα έχουμε:
6α/(α+β)= 10β/(α+β) —-> 6α=10β —-> α=10β/6
Διαιρούμε το κλάσμα δια του δύο κι’ έχουμε:
α=10β/6 —-> α=5β/3 (3)
Αντικαθιστούμε τη (3) στη (2) κι’ έχουμε:
υ=10β/(α+β) —-> υ=10β/[(5β/3)+β] —–> υ=10β/[(5β+3β)/3] —-> υ=10β/8β/3 —–>
υ=(3*10β)/8β —> υ=30β/8β –> υ=30/8 —> υ=3,75μ. (4)
(Γ)Γενίκευση για τυχαία μήκη πασσάλων.
Έστω ΑΒ=x, ΓΔ=ψ, ΕΚ=υ, ΑΚ=α, και ΚΓ=β
(i)Από την ομοιότητα των ορθογωνίων τριγώνων (ΑΓΔ) και (ΑΕΚ) έχουμε:
ΑΚ/ΑΓ=ΕΚ/ΓΔ —-> α/(α+β)=υ/ψ —-> αψ=υ*(α+β) —-> υ=αψ/(α+β) (1)
(ii)Από την ομοιότητα των ορθογωνίων τριγώνων (ΑΒΓ) και (ΕΚΓ) έχουμε:
ΚΓ/ΑΓ=ΕΚ/ΑΒ —-> β/(α+β)=υ/x —-> βx=υ*(α+β) —-> υ=βx/(α+β) (2)
Επειδή τα τρίγωνα είναι όμοια τα ύψη είναι ίσα, άρα έχουμε:
αψ/(α+β)=βx/(α+β) —> αψ=βx —> α=βx/ψ (3)
Αντικαθιστούμε τη (3) στη (2) κι’ έχουμε:
υ=βx/(α+β) —-> υ=βx/[(βx/ψ)+β] —–> υ=βx/[(βx+βψ)/ψ] —-> υ=βx/[β*(χ+ψ)]/ψ —->
υ=βxψ/β*(x+ψ) —-> υ=xψ(x+ψ) (4)
Άρα το ύψος, όπου διασταυρώνονται τα σχοινιά, παραμένει πάντα σταθερό, ανεξάρτητα από την απόσταση των πασσάλων(ΑΓ).
Ενδιαφέρον παρουσιάζει επίσης μια παραλλαγή
στην οποία τα μήκη είναι δεδομένα, στα σχοινιά, στο ύψος του σημείου της διασταύρωσης των σχοινιών από το έδαφος και ζητείται η απόσταση μεταξύ των δύο πασσάλων.
Στο βιβλίο του Martin Gardner “Το Τσίρκο των Μαθηματικών”,1990 εκδ. Τροχαλία, §3, σελίδα 53, ο Martin Gardner αναφέρει ότι η απλούστερη ακέραια λύση του προβλήματος είναι η εξής:
Μήκη σχοινιών:119μ. και 70μ.
Ύψος σημείου διασταύρωσης των σχοινιών από το έδαφος:30μ.
Απόσταση μεταξύ των πασσάλων:56μ.
Μήκη πασσάλων:105μ. και 42μ.
Επίσης ο Brian Bolt στο βιβλίο του «Mathematical Cavalcade», 1992 έκδοση Cambridge University Press, αναφέρει δύο παραλλαγές του προβλήματος Νο.92, σελίδα 77 και Νο.110, σελίδα 88.